PageRank 通过网页与网页之间的链接关系计算各网页权重,一般权重高的网页特点是:链接向它的网页数量多、链向它的网页其权重也较高。PageRank 就是通过这样的连接关系,一轮轮迭代计算后得出各网页的权重。
思路拓展一下,其实人与人之间也是连接着的,在社会的人际关系网中,每个人的社会地位和身价也是不同的。以微博为例,我们都有关注者和粉丝(类似网页之间的链接),可以发现所谓的“大V”基本上粉丝数量多,并且粉丝里不乏很多其他“大V”,所以这个帐号的价值就大。
同样博客园也具有类似的社交关系,用户可以选择“关注的人”以及“关注我的人”,理论上是可以用 PageRank 算法算出哪些用户更受大家欢迎,于是本文代大家八卦了一下,文章较长,只想看排名的同学请直接拉到末尾。。。
《数学之美》第10章的延伸阅读部分,对 PageRank 的计算方法进行了简单介绍,但原书有些错误,修改后描述如下:
我们设向量 B 为第一、第二…第N个网页的网页排名

矩阵 A 代表网页之间的权重输出关系,其中 amn 代表第 m 个网页向第 n 个网页的输出权重。

输出权重计算较为简单:假设 m 一共有10个出链,指向 n 的一共有2个,那么 m 向 n 输出的权重就为 2/10。
现在问题变为:A 是已知的,我们要通过计算得到 B。
假设 Bi 是第 i 次迭代的结果,那么
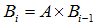
初始假设所有网页的排名都是 1/N (N为网页总数量),即
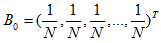
通过上述迭代计算,最终 Bi 会收敛,即 Bi 无限趋近于 B,此时 B = B × A。
假设有网页A、B、C、D,它们之间的链接关系如下图所示
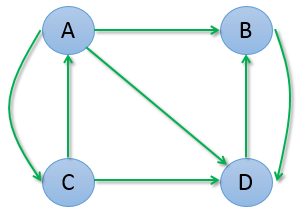
计算 B1 如下:

不断迭代,计算结果如下:
第 1次迭代: 0.125, 0.333, 0.083, 0.458
第 2次迭代: 0.042, 0.500, 0.042, 0.417
第 3次迭代: 0.021, 0.431, 0.014, 0.535
第 4次迭代: 0.007, 0.542, 0.007, 0.444
第 5次迭代: 0.003, 0.447, 0.002, 0.547
第 6次迭代: 0.001, 0.549, 0.001, 0.449
第 7次迭代: 0.001, 0.449, 0.000, 0.550
第 8次迭代: 0.000, 0.550, 0.000, 0.450
第 9次迭代: 0.000, 0.450, 0.000, 0.550
第10次迭代: 0.000, 0.550, 0.000, 0.450
... ...
我们可以发现,A 和 C 的权重变为0,而 B 和 D 的权重也趋于在 0.5 附近摆动。从图中也可以观察出:A 和 C 之间有互相链接,但它们又把权重输出给了 B 和 D,而 B 和 D之间互相链接,并不向 A 或 C 输出任何权重,所以久而久之权重就都转移到 B 和 D 了。
上面是最简单正常的情况,考虑一下两种特殊情况:
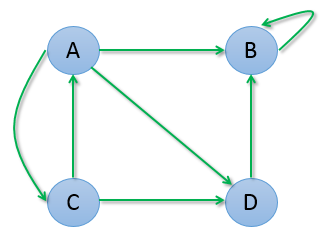

第一种情况是,B 存在导向自己的链接,迭代计算过程是:
第 1次迭代: 0.125, 0.583, 0.083, 0.208
第 2次迭代: 0.042, 0.833, 0.042, 0.083
第 3次迭代: 0.021, 0.931, 0.014, 0.035
第 4次迭代: 0.007, 0.972, 0.007, 0.014
第 5次迭代: 0.003, 0.988, 0.002, 0.006
第 6次迭代: 0.001, 0.995, 0.001, 0.002
第 7次迭代: 0.001, 0.998, 0.000, 0.001
第 8次迭代: 0.000, 0.999, 0.000, 0.000
第 9次迭代: 0.000, 1.000, 0.000, 0.000
第10次迭代: 0.000, 1.000, 0.000, 0.000
... ...
我们发现最终 B 权重变为1,其它所有网页的权重都变为了0 =。=!
第二种情况是 B 是孤立于其它网页的,既没有入链也没有出链,迭代计算过程是:
第 1次迭代: 0.125, 0.000, 0.125, 0.250
第 2次迭代: 0.063, 0.000, 0.063, 0.125
第 3次迭代: 0.031, 0.000, 0.031, 0.063
第 4次迭代: 0.016, 0.000, 0.016, 0.031
第 5次迭代: 0.008, 0.000, 0.008, 0.016
第 6次迭代: 0.004, 0.000, 0.004, 0.008
第 7次迭代: 0.002, 0.000, 0.002, 0.004
第 8次迭代: 0.001, 0.000, 0.001, 0.002
第 9次迭代: 0.000, 0.000, 0.000, 0.001
第10次迭代: 0.000, 0.000, 0.000, 0.000
... ...
我们发现所有网页权重都变为了0 =。=!
出现这种情况是因为上面的数学模型出现了问题,该模型认为上网者从一个网页浏览下一个网页都是通过页面的超链接。想象一下正常的上网情景,其实我们在看完一个网页后,可能直接在浏览器输入一个网址,而不通过上一个页面的超链接。
我们假设每个网页被用户通过直接访问方式的概率是相等的,即 1/N,N 为网页总数,设矩阵 e 如下:
![]()
设用户通过页面超链接浏览下一网页的概率为 α,则直接访问的方式浏览下一个网页的概率为 1 - α,改进上一节的迭代公式为:
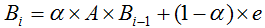
通常情况下设 α 为0.8,上一节”具体示例”的计算变为如下:
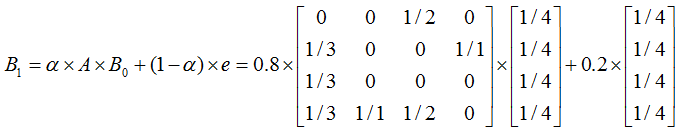
迭代过程如下:
第 1次迭代: 0.150, 0.317, 0.117, 0.417
第 2次迭代: 0.097, 0.423, 0.090, 0.390
第 3次迭代: 0.086, 0.388, 0.076, 0.450
第 4次迭代: 0.080, 0.433, 0.073, 0.413
第 5次迭代: 0.079, 0.402, 0.071, 0.447
第 6次迭代: 0.079, 0.429, 0.071, 0.421
第 7次迭代: 0.078, 0.408, 0.071, 0.443
第 8次迭代: 0.078, 0.425, 0.071, 0.426
第 9次迭代: 0.078, 0.412, 0.071, 0.439
第10次迭代: 0.078, 0.422, 0.071, 0.428
第11次迭代: 0.078, 0.414, 0.071, 0.437
第12次迭代: 0.078, 0.421, 0.071, 0.430
第13次迭代: 0.078, 0.415, 0.071, 0.436
第14次迭代: 0.078, 0.419, 0.071, 0.431
第15次迭代: 0.078, 0.416, 0.071, 0.435
第16次迭代: 0.078, 0.419, 0.071, 0.432
第17次迭代: 0.078, 0.416, 0.071, 0.434
第18次迭代: 0.078, 0.418, 0.071, 0.432
第19次迭代: 0.078, 0.417, 0.071, 0.434
第20次迭代: 0.078, 0.418, 0.071, 0.433
... ...
互联网的网页数量是 Billion 级别的,所以不可能一下子初始化矩阵 A ,试想一下 10亿 × 10亿 的矩阵是什么概念!
这时就用到稀疏矩阵了,定义稀疏矩阵的结构如下(其实是稀疏矩阵的一行):
public class SparseMatrix<T> { public SparseMatrix(T head, double rank) { Head = head; LinkedItems = new List<T>(); Rank = rank; } /// <summary> /// 稀疏矩阵头 /// </summary> public T Head { get; private set; } public double Rank { get; set; } /// <summary> /// 稀疏矩阵链接的项目 /// </summary> public List<T> LinkedItems { get; set; } public void AddLink(T linkedItem) { LinkedItems.Add(linkedItem); } }
第一节中的链接示例图,就可以用如下代码表示:
Dictionary<char, SparseMatrix<char>> matrix = new Dictionary<char, SparseMatrix<char>> { {'A', new SparseMatrix<char>('A', 0.25){LinkedItems = new List<char>{'B', 'C', 'D'}}}, {'B', new SparseMatrix<char>('B', 0.25){LinkedItems = new List<char>{'D'}}}, {'C', new SparseMatrix<char>('C', 0.25){LinkedItems = new List<char>{'A', 'D'}}}, {'D', new SparseMatrix<char>('D', 0.25){LinkedItems = new List<char>{'B'}}} };
通过稀疏矩阵计算,与原先的整个矩阵行列式计算有较大不同,计算次序已经发生了变化。原先矩阵是一行乘以权重的竖列,稀疏矩阵则变为类似于按原先矩阵的竖列与权重相乘。矩阵运算中当然不允许 1 × N 矩阵与 1 × N 矩阵相乘的情况,我们能做的就是先将一项项算好,比如先算 A 这一行,算出 A 给 B、C、D输出多少权重,在一个类似字典类型的数据结构里,给 B、C和 D 各加上一笔,像是一个 Map-Reduce 过程。
public class MapReduce<T> { private readonly Dictionary<T, double> _map; public MapReduce() { _map = new Dictionary<T, double>(); } public double Reduce(T key, double value) { if (_map.ContainsKey(key)) { _map[key] += value; return _map[key]; } _map.Add(key, value); return value; } public double GetOrSetDefaultValue(T key) { if (_map.ContainsKey(key)) return _map[key]; _map.Add(key, 0.0); return 0.0; } }
PageRank 设计如下:
public class PageRank<T> { private MapReduce<T> _mapReduce; private readonly double _stayProbability; private readonly double _averageRank; /// <summary> /// /// </summary> /// <param name="totalCount">项目总数</param> /// <param name="stayProbability">保持留在某个项目, 不跳转的概率</param> public PageRank(int totalCount, double stayProbability = 0.8) { _mapReduce = new MapReduce<T>(); _stayProbability = stayProbability; _averageRank = 1.0 / totalCount; } /// <summary> /// 计算下一轮PageRank /// </summary> public void NextCircle() { _mapReduce = new MapReduce<T>(); } /// <summary> /// 计算一条行列式 /// </summary> /// <param name="sparseMatrix">稀疏矩阵</param> public void Calc(SparseMatrix<T> sparseMatrix) { var outputRank = 1.0 / sparseMatrix.LinkedItems.Count; foreach (var item in sparseMatrix.LinkedItems) { _mapReduce.Reduce(item, _stayProbability * outputRank * sparseMatrix.Rank); } //当没有其它链接指向Head的时候, 以防漏项 _mapReduce.Reduce(sparseMatrix.Head, (1 - _stayProbability) * _averageRank); } /// <summary> /// 一轮PageRank迭代之后, 获取最新的PageRank并更新 /// </summary> /// <param name="key"></param> /// <returns></returns> public double GetCurrentRank(T key) { return _mapReduce.GetOrSetDefaultValue(key); } }
调用示例:
var matrix = new Dictionary<char, SparseMatrix<char>> { {'A', new SparseMatrix<char>('A', 0.25){LinkedItems = new List<char>{'B', 'C', 'D'}}}, {'B', new SparseMatrix<char>('B', 0.25){LinkedItems = new List<char>{'D'}}}, {'C', new SparseMatrix<char>('C', 0.25){LinkedItems = new List<char>{'A', 'D'}}}, {'D', new SparseMatrix<char>('D', 0.25){LinkedItems = new List<char>{'B'}}} }; var pageRank = new PageRank<char>(matrix.Count); //计算30轮 for (int i = 1; i <= 30; i++) { pageRank.NextCircle(); foreach (var item in matrix) { pageRank.Calc(item.Value); } foreach (var item in matrix) { var cRank = pageRank.GetCurrentRank(item.Key); item.Value.Rank = cRank; } var str = string.Join(", ", matrix.Select(item => item.Value.Rank.ToString("N3"))); Console.WriteLine(string.Format("第{0,2}次迭代: {1}", i, str)); }
开源地址:https://github.com/CreateChen/PageRank
写一个简单的网络爬虫,爬取博客园所有用户的 Id、关注的人等信息(过程略),最终得到如下结构的表格:

首先八卦一下粉丝数量 Top 20,方便与 PageRank 算出的结果做对比。
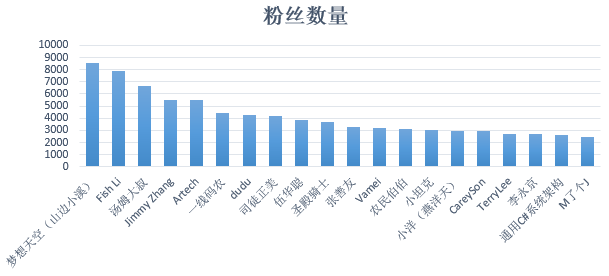
下面进入真正的 PageRank 计算了,利用第二节的程序计算,一次迭代计算速度很快,从数据库获取数据并且计算完毕只要6秒,更新数据库的 Rank 字段需要近30秒。下表展示的是第1轮迭代、第15轮的用户的权重:
排名 NickName Rank … NickName Rank 1 梦想天空(山 0.002165 … 梦想天空(山 0.001346 2 Fish Li 0.00192 … dudu 0.001334 3 汤姆大叔 0.001514 … Artech 0.00102 4 Jimmy Zhang 0.001281 … Fish Li 0.000947 5 M了个J 0.001244 … 司徒正美 0.000786 6 Artech 0.001164 … 李永京 0.000746 7 农民伯伯 0.001161 … 汤姆大叔 0.0007 8 司徒正美 0.000987 … 趣味苹果开发 0.000677 9 Vamei 0.000953 … 通用C#系统架 0.000601 10 tornadomeet 0.000858 … M了个J 0.00059 11 伍华聪 0.000787 … Jimmy Zhang 0.000586 12 一线码农 0.000786 … banban 0.000576 13 吴秦 0.00075 … Milo Yip 0.000532 14 dudu 0.000729 … 张善友 0.000488 15 虫师 0.000722 … Jeffrey Zhao 0.00047 16 小坦克 0.000691 … 觉先 0.000462 17 Rollen Holt 0.000649 … SoftwareTeac 0.000444 18 圣殿骑士 0.000545 … 博客园团队 0.000434 19 CareySon 0.000538 … TerryLee 0.000434 20 文顶顶 0.000538 … 胡尐睿丶 0.00043 21 小洋(燕洋天 0.000535 … T2噬菌体 0.000422 22 虾皮 0.000529 … 农民伯伯 0.000415 23 JerryLead 0.000526 … Anytao 0.000411 24 李永京 0.000508 … 圣殿骑士 0.000411 25 方倍工作室 0.000505 … 深蓝色右手 0.000406 26 cloudgamer 0.000486 … 伍华聪 0.0004 27 杨中科 0.000483 … 一线码农 0.000399 28 TerryLee 0.000467 … 小洋(燕洋天 0.000388 29 张善友 0.000466 … Cat Chen 0.000374 30 深蓝色右手 0.000457 … CareySon 0.000371 31 谦虚的天下 0.000445 … Vamei 0.000365 32 通用C#系统架 0.000435 … ziqiu.zhang 0.000358 33 胡尐睿丶 0.00042 … 周 金根 0.000351 34 三生石上 0.000413 … 伍迷 0.000342 35 KenshinCui 0.000397 … xiaotie 0.000332 36 博客园团队 0.000389 … 谦虚的天下 0.000331 37 酸奶小妹 0.000387 … 冠军 0.000329 38 Milo Yip 0.000372 … 吴秦 0.000327 39 伍迷 0.00037 … cloudgamer 0.000318 40 子龙山人 0.000369 … tornadomeet 0.000305 41 Insus.NET 0.000369 … 酸奶小妹 0.0003 42 菩提树下的杨 0.000369 … 小坦克 0.0003 43 万一 0.000368 … 【当耐特】 0.000285 44 _Luc_ 0.000367 … chenkai 0.000277 45 夏天的森林 0.000354 … Justin 0.000274 46 ziqiu.zhang 0.000351 … 装配脑袋 0.000272 47 Jeffrey Zhao 0.000351 … 虫师 0.000271 48 叶小钗 0.000343 … 菩提树下的杨 0.000271 49 真 OO无双 0.000343 … Gnie 0.00027 50 SoftwareTeac 0.000337 … 张逸 0.000252 51 webabcd 0.000333 … LeftNotEasy 0.000245 52 T2噬菌体 0.000331 … 小静(Cathy 0.00024 53 Ruthless 0.000328 … Gray Zhang 0.000237 54 peida 0.000327 … Jesse Liu 0.000237 55 陈梓瀚(vczh) 0.000324 … JerryLead 0.000231 56 聂微东 0.000322 … webabcd 0.000228 57 Jesse Liu 0.000317 … fly in ocean 0.000225 58 【当耐特】 0.000288 … Anders Cui 0.000221 59 西西吹雪 0.000286 … 代震军 0.000221 60 snandy 0.000286 … COM张 0.00022 61 Phinecos(洞 0.000286 … 楠小楠 0.00021 62 David_Tang 0.000283 … 何戈洲 0.00021 63 yangecnu 0.000282 … 三生石上 0.000207 64 孤傲苍狼 0.000278 … 路过秋天 0.000204 65 Learning har 0.000277 … Jake Lin 0.000203 66 Stephen_Liu 0.000272 … 飞洋过海 0.000201 67 Terry_龙 0.000269 … 陈希章 0.0002 68 xiaotie 0.000269 … 叶小钗 0.000198 69 Leo Chin 0.000269 … eaglet 0.000197 70 海 子 0.000267 … 陈梓瀚(vczh) 0.000197 71 Barret Lee 0.000264 … _Luc_ 0.000194 72 路过秋天 0.000263 … snandy 0.000191 73 Dsp Tian 0.000255 … 新瓶老酒 0.000186 74 Devin Zhang 0.000255 … Bēniaǒ 0.000185 75 苍梧 0.000252 … dax.net 0.000185 76 觉先 0.000251 … 麒麟.NET 0.000185 77 周 金根 0.00025 … 方倍工作室 0.000183 78 冠军 0.000249 … 万一 0.000181 79 何戈洲 0.000242 … 陈硕 0.000179 80 刘冬.NET 0.000237 … 任力 0.000177 81 hoojo 0.000236 … Franky 0.000177 82 Orisun 0.000236 … 虾皮 0.000173 83 CrazyBingo 0.000235 … Stephen_Liu 0.000172 84 代震军 0.000234 … 石破天惊 0.000172 85 minglz 0.000231 … 岑安 0.000171 86 Alexia(minmi 0.000226 … 杨中科 0.00017 87 Gnie 0.000226 … iOS之旅 0.00017 88 邹华栋 0.000225 … 横刀天笑 0.000169 89 Samaritans 0.000224 … 邀月 0.000168 90 Aaron艾伦 0.000222 … jv9 0.000165 91 邀月 0.000221 … 聂微东 0.000164 92 Healtheon 0.000219 … 创想中国(羲闻 0.000164 93 李林峰的园子 0.000219 … CoderZh 0.000163 94 吕震宇 0.000218 … Luminji 0.000163 95 沈逸 0.000218 … winter-cn 0.000163 96 LeftNotEasy 0.000213 … Rollen Holt 0.000161 97 陈希章 0.000212 … 金色海洋(jy 0.000159 98 Hongten 0.000211 … 重典 0.000159 99 创想中国(羲闻 0.000211 … 阿一(杨正祎) 0.000157 100 Cat Chen 0.000208 … 夜里的烟 0.000157如果你对完整的计算过程感兴趣,可以下载完整表格。想了解自己的权重及排名请在下方留言。
当然在实际计算排名过程中,不单单依据粉丝与关注者之间的关系,还需要结合文章的质量、更新频率及数量,最后给一个综合的评分。总之:被关注数量越多、经常写文章、文章被赞的次数越多、评论次数多,就越能提升社区影响力。
本文链接:http://www.cnblogs.com/technology/p/PageRank.html