C#及Java递归方法实现Hanoi塔(汉诺塔)问题_JAVA_编程开发_程序员俱乐部

今天，在学习C#的时候，遇到了一个很有意思很经典的问题--Hanoi塔(汉诺塔)问题。于是就研究了一下子，现在小小的总结一下。

(1)问题的描述

古代有一个梵塔，塔内有3个座，分别用A、B、C表示。开始时A座有N个盘子，盘子两两大小不等，大的在下，小的在上，盘子编号从上到下分别编号为1到N。B座，C座上面没有盘子。要求将这N个盘子从A移到C上，且在移动的过程中大盘不能压在小盘上。移动过程可以借助B盘中转。

(2)问题的分析

这是一个典型的递归问题，将A转移到C，可以分为下面的这些步骤：

1.如果N=1，那么只需要将盘子从A移到C即可。所以，N=1也是递归终止条件。

2.如果N>1，那么将N-1个盘子从A移到B，利用C做中转。再将第N个盘子从A移到C。

3.接下来，就变成了一个N-1个盘子从B移到C的，A为中转的汉诺塔问题了，就可以直接递归了。

(3)问题的实现

那么，在实现的时候，我用了以前学习的Java和最近正在学习的C#语言来实现它，其实两种语言差不多，在实现这个问题的具体算法上，没有很大的不同。

1.C#版本实现

class="c#" name="code">using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace Hanoi
{
    class Program
    {
        //总共搬动盘子的次数
        static int count = 0;
       
        /*
         *程序入口 
         */
        static void Main(string[] args)
        {
            Console.Write("请输入Hanoi塔问题的盘子数目：");
            int n = int.Parse(Console.ReadLine());
            Hanoi(n,'A','B','C');
            Console.WriteLine("移动结束，一共进行了{0}次移动",count);
            Console.ReadLine();
        }


        /*
        *输出一个移动步骤的方法 
        */
        public static void PrintMove(char x, char y)
        {
            Console.WriteLine("{0}-->{1}", x, y);
        } 

        /*
         Hanoi塔递归方法，n是盘子数，one，two，three是3个座
         */
        public static void Hanoi(int n,char one,char two,char three) {

            if (n == 1)
            {
                ++count;
                PrintMove(one, three);
                return;
            }
            else {
                ++count;
                //把N-1个盘子拿到中转座
                Hanoi(n-1,one,three,two);
                //将第N个盘子移到目标座
                PrintMove(one,three);
                //把中转座上的N-1个盘子移到目标座
                Hanoi(n-1,two,one,three);
            }
        }
    }
}

?运行结果：

?

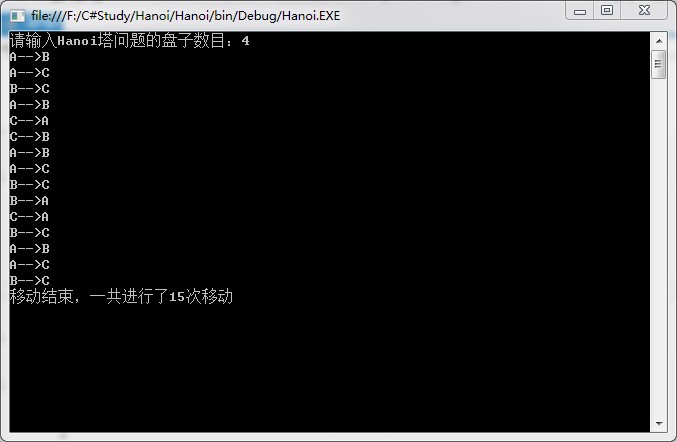
1.Java版本实现

import java.util.Scanner;

  /**
	 * 汉诺塔问题
	 * xiangpin
	 */
public class Hanoi {
	
	//计算搬动盘数目
	public static int count=0;
	/**
	 * 程序入口
	 * @param args
	 */
	public static void main(String[] args) {

	//从键盘读取数据
		System.out.println("请输入汉诺塔问题的盘子数目：");
		Scanner scan=new Scanner(System.in);
		int n=scan.nextInt();
		Hanoi(n,'A','B','C');
		System.out.println("移动结束，一共移动了"+count+"次");
	}
	
	/**
	 * 输出移动步骤的方法
	 */
	public static void PrintMove(char x,char y){
		System.out.println("从"+x+"移动到"+y);
		
	}
	
	/**
	 * 汉诺塔的递归方法，n是盘子数，one，two,three是3个座
	 */
	public static void Hanoi(int n ,char A,char B,char C){
		//如果N=1，则直接从A搬到C
		if(n==1){
			++count;
			PrintMove(A,C);
			
		}
		else{
			++count;
			//如果n>1，则将n-1个盘子，从A搬到B，C作为中转
			Hanoi(n-1,A,C,B);
			//再将第n个盘子搬到C
			PrintMove(A,C);
			//现在问题变成n-1个盘子，从B到C，A为中转的问题了，运用递归
			Hanoi(n-1,B,A,C);	
		}
	}
}

?运行结果：

?通过这个例子可以很容易的看出来，利用递归可以很快速且有效的得出结果。另外，我觉得将一种自己较为熟悉的语言和另外一种新学的结合起来学习，是一件很有趣的事情。

• 
• 大小: 32.7 KB

• 
• 大小: 24.9 KB

• 查看图片附件