您所在的位置：程序员俱乐部 > 编程开发 > .NET > 根据字典和指定长度，按排列组合生成字符串（七个方案）

根据字典和指定长度，按排列组合生成字符串（七个方案）

2013/9/3 13:13:50 uonun 博客园我要评论(0)

摘要：命题根据指定的字符集合（字典），按排列组合的规则（允许重复），生成指定长度的所有字符串。如下代码：classProgram{staticvoidMain(string[]args){stringdic="abcdef";intlen=3;inttop_last_N=5;IGeneratorg=newGenerator1();varresult=g.Generate(dic,len)??newList<string>();Console.WriteLine
标签：字符串

命题

根据指定的字符集合（字典），按排列组合的规则（允许重复），生成指定长度的所有字符串。如下代码：

class="code">class Program
{
    static void Main(string[] args)
    {
        string dic = "abcdef";
        int len = 3;
        int top_last_N = 5;

        IGenerator g = new Generator1();

        var result = g.Generate(dic, len) ?? new List<string>();
        Console.WriteLine("{0} strings generated:", result.Count);

        PrintTheResult(top_last_N, result);

        Console.ReadKey();
    }

    private static void PrintTheResult(int top_last_N, List<string> result)
    {
        if (result.Count > top_last_N * 2)
        {
            for (int i = 0;i < top_last_N;i++)
            {
                Console.WriteLine(result[i]);
            }
            Console.WriteLine("......");
            for (int i = result.Count - top_last_N;i < result.Count;i++)
            {
                Console.WriteLine(result[i]);
            }
        }
        else
        {
            foreach (var s in result)
            {
                Console.WriteLine(s);
            }
        }
    }
}

interface IGenerator
{
    List<string> Generate(string dic, int length);
}

class Generator1 : IGenerator
{
    public List<string> Generate(string dic, int length)
    {
        // we should implement this method
        throw new NotImplementedException();
    }
}

举个例子，比如：字典为[a,b,c]，指定长度为 2，则生成的所有字符串应当为：

"aa","ab","ac","ba",……,"ca","cb","cc"，总计9个字符串。

那么程序里我们应当怎么来生成这些字符串呢？如下循序渐进地列出解决方案。

投石问路：假设长度固定
方案一：我们来多循环几次（循环拼接字符串）
方案二：不用字符串，使用不安全代码（循环拼接字符串Unsafe版）
方案三：换个角度看问题（字符串模拟数字依次循环进行进制转换）
方案四：小学的加法运算正闪闪发光（字符串模拟数字依次自增+1）
方案五：再次改写，不用字符串，使用不安全代码（字符串模拟数字依次自增+1的Unsafe版）
方案六：闲来没事（1）：Fixed-point combinator
方案七：闲来没事（2）：Fixed-point combinator + Unsafe 双剑合璧

投石问路：假设长度固定

命题中有三个关键要素：字典、长度、排列组合（允许重复）。

首先我们假定长度固定，比如长度为“3”，直接使用给定的字典进行排列组合就行了。

既然是排列组合，我首先想到的是循环，于是有：

class Generator1 : IGenerator
{
    public List<string> Generate(string dic, int length)
    {
        // since we deal with the "length" as a constant parameter, so we leave it alone.
        var result = new List<string>();

        foreach (var x in dic)
        {
            foreach (var y in dic)
            {
                foreach (var z in dic)
                {
                    result.Add(string.Format("{0}{1}{2}", x, y, z));
                }
            }
        }

        return result;
    }
}

长度为3，那么我们用3个循环生成每一位的字符，然后拼凑起来，这简直太简单了，运行效果如下：

OK，好了，如果考虑长度为呢？长度直接关系到需要循环的次数，完了，我们的循环都是写死在代码里的，我们怎么知道传进来的长度参数值是多少，需要循环多少次啊？

方案一：我们来多循环几次

说实在的，我觉得循环就是一个玩命却又任劳任怨的苦工。无论多么深、多么广、多么耗时的循环，他都能反反复复、机机械械地去执行，要么执行完成，要么累死——资源耗尽。

对于上文中的 Generate 方法，我们需要根据参数来确定循环的次数，那么我们定义一个方法专门来做循环，然后根据参数的值来运行若干次。

仔细观察我们的第一次实现，除第一次循环之外，每一次的循环都是在之前循环得到的字符串基础上，追加一个字符，从而实现“拼凑”到足够长度的目的。那么第一次呢？其实第一次的循环就只是从依次从字典里取出每一个字符，放到结果集里，作为后续“拼凑”动作的种子。因此，首先，我们需要一个种子，循环在这个基础上进行，有了种子之后，就从种子的每一个元素上，发芽（分化）出第二次的“拼凑”...直到N次——看起来，这已经是一个树的生成了，只不过这个树比较特殊，每一个节点的分支数都一样。

好了，见代码：

class Generator2LoopSegments : IGenerator
{
    public List<string> Generate(string dic, int length)
    {
        List<string> result = null;
        for (int i = 0;i <= length;i++)
        {
            result = Loop(dic, result);
        }
        return result;
    }

    private List<string> Loop(string dic, List<string> seed)
    {
        var result = new List<string>();
        if (seed == null || seed.Count == 0)
        {
            // for the first time, we just choose one char only to fill full into the List.
            // result.AddRange(from c in dic select c.ToString());
            result.Add(string.Empty);
        }
        else
        {
            for (int i = 0;i < seed.Count;i++)
            {
                foreach (var c in dic)
                {
                    result.Add(string.Format("{0}{1}", seed[i], c));
                }
            }
        }

        return result;
    }

    public override string ToString()
    {
        return "Loop segments";
    }
}

好了，完美无瑕，实现了命题中要求的排列组合！不过，等等，咦，怎么当我 length 设为 5 的时候，竟然抛出 OutOfMemoryException 的异常了？内存占用很高啊！嗯，是不是因为编译成了 32 位程序的原因？改成 64 位试试？哈，行了，不过内存竟然占用了 3G！

Tips:

编译为32位程序，在64位Win7系统中运行，当内存占用接近2G时，程序即抛出 OutOfMemoryException 的异常，直接表现为无法创建字符串或无法向集合添加新项。

运行是能运行了，不过时间上貌似不尽人意，运行太久了，是不是还能有提高呢？怎么办呢？这里使用了大量字符串，对字符串的操作也非常多，要不咱不使用字符串，直接使用 char* 试试？

方案二：不用字符串，使用不安全代码

思路和上面的解决方案一致，只是对上面字符串相关的操作进行了修改，使用不安全代码 unsafe 。

class Generator2LoopSegmentsUnsafe : IGenerator
{
    public unsafe List<string> Generate(string dic, int length)
    {
        char*[] result = null;
        for (int i = 0;i < length;i++)
        {
            result = Loop(dic, result);
        }

        var list = new List<string>();
        if (result != null)
        {
            foreach (var p in result)
            {
                var aa = new String(p);
                list.Add(aa);
            }
        }
        return list;
    }

    private unsafe char*[] Loop(string dic, char*[] seed)
    {
        char*[] result = null;
        if (seed == null || seed.Length == 0)
        {
            result = new char*[dic.Length];
            // for the first time, we just choose one char only to fill full into the List.
            for (int i = 0;i < dic.Length;i++)
            {
                IntPtr p = Marshal.AllocHGlobal(sizeof(char));
                result[i] = (char*)p.ToPointer();
                *result[i] = dic[i];
                // string will/should be end with the char '\0'.
                *(result[i] + 1) = '\0';
            }
        }
        else
        {
            result = new char*[seed.Length * dic.Length];
            int n = 0;
            for (int i = 0;i < seed.Length;i++)
            {
                foreach (var c in dic)
                {
                    IntPtr p = Marshal.AllocHGlobal(sizeof(char));
                    result[n] = (char*)p.ToPointer();
                    *(result[n]) = *seed[i];

                    int j = 0;
                    // string will/should be end with the char '\0'.
                    while (*(seed[i] + ++j) != '\0')
                    {
                        *(result[n] + j) = *(seed[i] + j);
                    }
                    *(result[n] + j) = c;
                    // string will/should be end with the char '\0'.
                    *(result[n] + j + 1) = '\0';
                    n++;
                }
            }
        }
        return result;
    }

    public override string ToString()
    {
        return "Loop segments(unsafe)";
    }
}

运行结果如下：

OK，从结果来看和上一个版本一致，不过时间和内存占用都不一样了！时间上少了很多，内存占用貌似不减反增，我猜想应当是因为 framework 中对字符串的处理比我手写得高端大气上档次一些吧……

到这里，看起来已经没太多的提升空间了，毕竟我们连这么高端的不安全代码都用了。

果然是这样吗？唉，别忘记了基础的东西，这玩意的时间复杂度有点高啊？（O(N^3)？猜的。时间复杂度这玩意，我一直没怎么看过...如果不对，请不吝赐教....）

嗯，能不能有个更简单的算法，让它的时间复杂度更低呢？

方案三：换个角度看问题（字符串模拟数字依次循环进行进制转换）

其实，如果细心你可能发现，这个排列组合，如果我们把字典换一下……

比如 [0,1]，长度 3，这将得到：000，001，010，011，100，101，110，111

比如 [0-9]，长度 2，这将得到：00,01,02,03,04,…,97,98,99

我去~这是啥？这不就是连续的整数么？

嗯，我们再看看，比如字典为 [0-9A-F]，长度 2，这将得到：00,01,02,...,09,0A,0B,...,0F,10,11,...,1A,1B,...,1F,20,21,...,FD,FE,FF

这，依然是连续整数，只不过是十六进制而已！

说到这里，其实你已经看出来了，上面依次就是二进制，十进制和十六进制。当他们是这些情况时，我们想排列组合，那岂不是易如反掌？让数字递增加一，直接一个循环就输出搞定了！

嗯，好办法，继续看，当字典为任意字符集的时候，可以吗？答案当然是可以的。[0-9A-F] 是十六进制，那 [0-9A-Z] 则自然是36进制！

既然如此，那我们的“排列组合”算法，就成了进制转换的算法了，囧。

参考：http://baike.baidu.com/link?url=q_M-tOHBN0XtyvdHBv-sk8vuV8dJf-Yna-7nRp1xwYQP-m2pj9CHV0x-u0nbChAN

好吧，代码来了：

class Generator3LoopAsNumbers : IGenerator
{
    public List<string> Generate(string dic, int length)
    {
        var fromBase = dic.Length;
        int min = 0, max = 0;
        if (fromBase > 1)
        {
            max = (int)Math.Pow(fromBase, length) - 1;
        }
        else
        {
            max = min;
        }

        //Console.WriteLine("min = {0}, max = {1}", min, max);

        var result = new List<string>();
        for (var current = min;current <= max;current++)
        {
            var tmp = "";
            for (var j = length - 1;j >= 0;j--)
            {
                var last = (int)(current % Math.Pow(fromBase, j + 1) / Math.Pow(fromBase, j));
                tmp += dic[last];
            }

            result.Add(tmp);
        }

        return result;
    }

    public override string ToString()
    {
        return "Loop as numbers";
    }
}

运行如图：

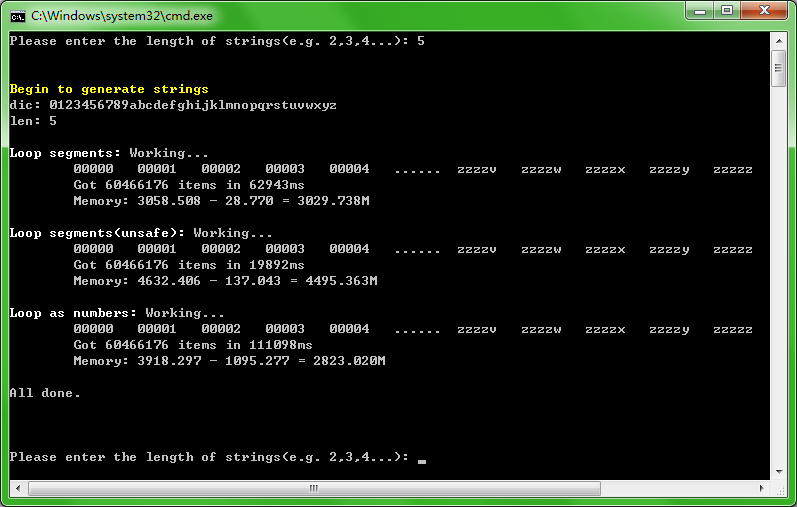
不过，好的想法不一定能运行出好的结果。按照这个解决方案，内存占用降了下来，但耗时却高了不少，将近第一个方案的两倍了，简直惨不忍睹！

正当我为之沮丧时，却突然又发现一丝曙光：既然我已经将这个排列组合看成是数字递增了，而且递增多少我也很清楚地知道，那为何我还要“劳心劳力”地去做进制转换呢？何不直接根据进制的规则，+1，+1，升位+1去做呢？小学加法啊！

说改就改！

方案四：小学的加法运算正闪闪发光（字符串模拟数字依次自增+1）

还记得小学时学的加法运算怎么算么？按小数点对齐，个位加个位，十位加十位，满10进一位。OK，按照这个思路再试一次看看，代码来了：

class Generator4GenerateNumbers : IGenerator
{
    public List<string> Generate(string dic, int length)
    {
        var result = new List<string>();
        string seed = new string(dic[0], length);
        result.Add(seed);
        while (GetNext(ref seed, seed.Length - 1, dic))
        {
            result.Add(seed);
        }

        return result;
    }

    private bool GetNext(ref string seed, int idx, string dic)
    {
        if (idx < 0 || idx >= seed.Length)
            return false;

        char c = seed[idx];
        if (dic.IndexOf(c) < dic.Length - 1)
        {
            c = dic[dic.IndexOf(c) + 1];
            seed = seed.Substring(0, idx) + c + seed.Substring(idx + 1, seed.Length - 1 - idx);
            return true;
        }
        else
        {
            c = dic[0];
            seed = seed.Substring(0, idx) + c + seed.Substring(idx + 1, seed.Length - 1 - idx);
            return GetNext(ref seed, idx - 1, dic);
        }
    }

    public override string ToString()
    {
        return "Generate numbers";
    }
}

当然，可以从代码中看出来，我们这里的加法运算太简单了，简单到第二个因子是 1，也就是每次运算加法只是数字递增1而已。其中dic[0]表示了每位可能的最小的数，相应地，dic[dic.Length-1]表示了没位可能的最大的数。

我们来运行试试：

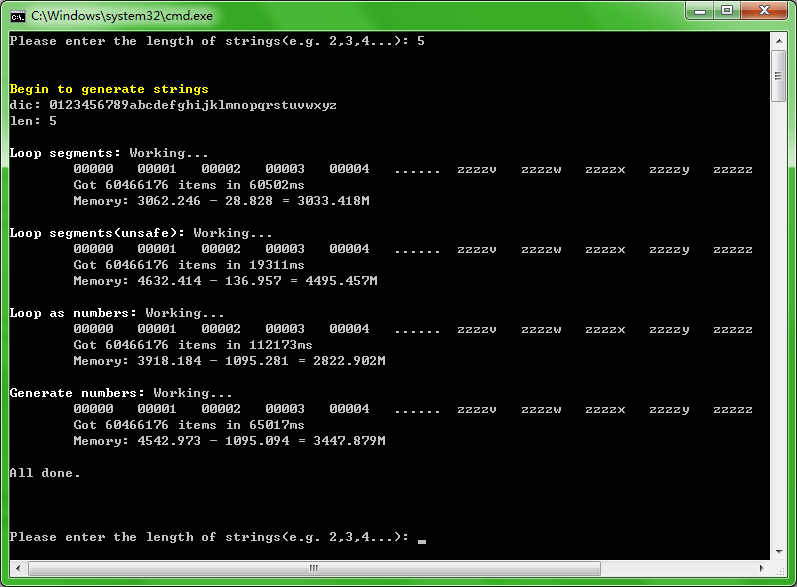
成是成了，不过……这个结果依然有点惨！效率不高，内存占用仍然居高不下，看来这闪闪的光——要不是我还没发掘出来，那就是我眼花了？嗯……要不再改写成非安全代码试试？

方案五：再次改写，不用字符串，使用不安全代码

照例，算法思路和上面一样，只是改写成非安全代码：

class Generator4GenerateNumbersUnsafe : IGenerator
{
    public List<string> Generate(string dic, int length)
    {
        var result = new List<string>();
        unsafe
        {
            IntPtr p = Marshal.AllocHGlobal(sizeof(char));
            var seed = (char*)p.ToPointer();
            int i = 0;
            for (;i < length;i++)
            {
                *(seed + i) = dic[0];
            }
            *(seed + i) = '\0';

            do
            {
                result.Add(new string(seed));
            } while (GetNext(ref seed, length - 1, dic));
        }

        return result;
    }

    private unsafe bool GetNext(ref char* seed, int idx, string dic)
    {
        int len = 0;
        for (;*(seed + len) != '\0';len++) { }
        if (idx < 0 || idx >= len)
            return false;

        char c = seed[idx];
        if (dic.IndexOf(c) < dic.Length - 1)
        {
            c = dic[dic.IndexOf(c) + 1];
            *(seed + idx) = c;
            return true;
        }
        else
        {
            c = dic[0];
            *(seed + idx) = c;
            return GetNext(ref seed, idx - 1, dic);
        }
    }

    public override string ToString()
    {
        return "Generate numbers(unsafe)";
    }
}

哈，看起来效果不错哦，时间和空间的占用都有提升，并且效果比第二个方案还好！

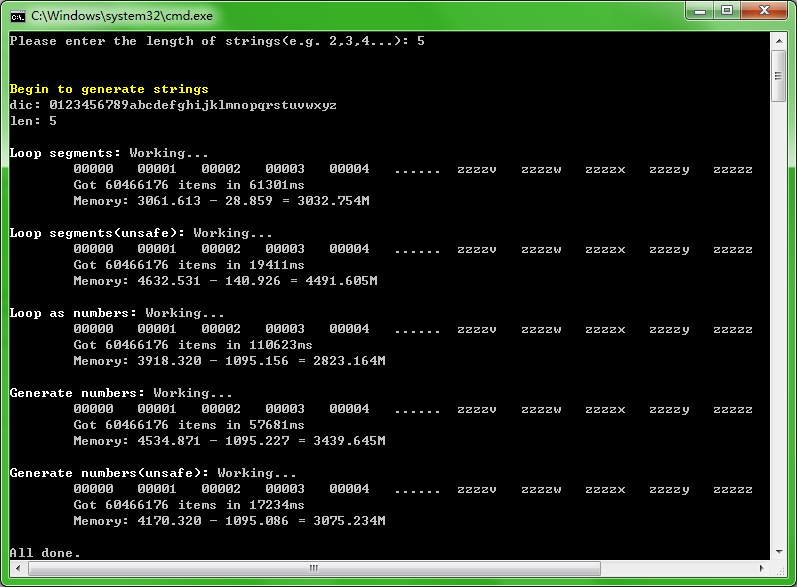
好了，算法的尝试到此为止。

下面来点无聊的东西：不动点组合子。

方案六：闲来没事（1）：Fixed-point combinator

关于 Fixed-point combinator 可以参考：

http://en.wikipedia.org/wiki/Fixed-point_combinator

http://zh.wikipedia.org/wiki/%E4%B8%8D%E5%8A%A8%E7%82%B9%E7%BB%84%E5%90%88%E5%AD%90

如下只是使用 Fixed-point combinator 对上一个解决方案的改写，效率更加底下，或许有提升空间……或许……

class Generator4GenerateNumbersFixedPoint : IGenerator
{
    public List<string> Generate(string dic, int length)
    {
        var result = new List<string>();
        var seed = new string(dic[0], length);
        while (!string.IsNullOrEmpty(seed))
        {
            result.Add(seed);

            seed = FixedPointCombinator(
            x =>
            {
                if (x != null)
                {
                    return (s, idx, idc) =>
                    {
                        if (idx < 0 || idx >= s.Length)
                            return null;

                        char c = s[idx];
                        if (dic.IndexOf(c) < dic.Length - 1)
                        {
                            c = dic[dic.IndexOf(c) + 1];
                            s = s.Substring(0, idx) + c + s.Substring(idx + 1, s.Length - 1 - idx);
                        }
                        else
                        {
                            c = dic[0];
                            s = s.Substring(0, idx) + c + s.Substring(idx + 1, s.Length - 1 - idx);
                            s = x(s, idx - 1, dic);
                        }

                        return s;
                    };
                }

                return null;
            })(seed, seed.Length - 1, dic);
        }

        return result;
    }

    private Func<string, int, string, string> FixedPointCombinator(
        Func<Func<string, int, string, string>, Func<string, int, string, string>> f1)
    {
        return (x, y, z) => f1(FixedPointCombinator(f1))(x, y, z);
    }

    public override string ToString()
    {
        return "Generate numbers(Fixed-Point Y)";
    }
}

注意，下面的代码可以编译通过，不过这……是个死循环，在构造 Fixed-Point Y 时，尤其需要注意：

private Func<string, int, string, string> Combinator_Recursive(
    Func<Func<string, int, string, string>, Func<string, int, string, string>> f1)
{
    return f1(Combinator_Recursive(f1));
}

惯例，贴出运行结果：

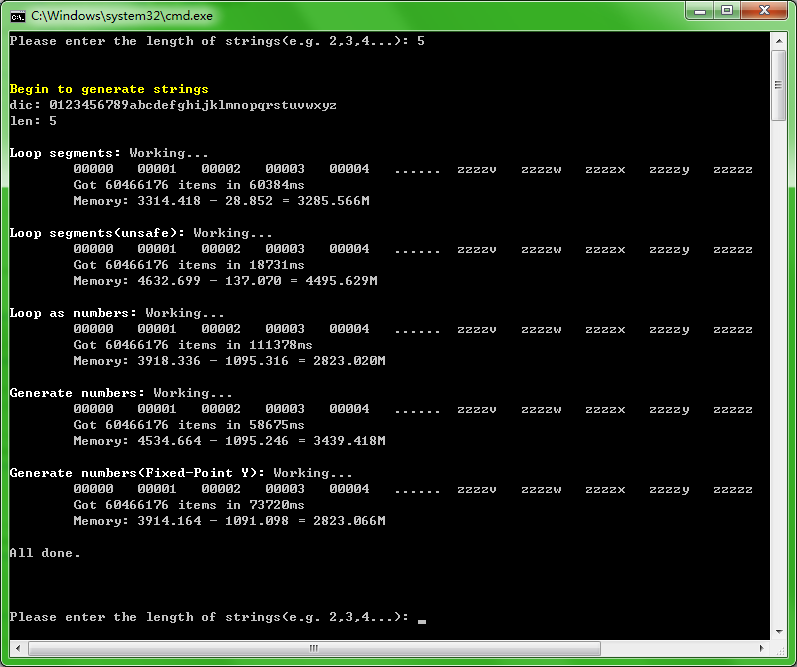
看样子，运行效果不尽人意。

方案七：闲来没事（2）：Fixed-point combinator + Unsafe 双剑合璧

当然，Fixed-point combinator 也有 Unsafe 版本：

class Generator4GenerateNumbersFixedPointUnsafe : IGenerator
{
    public List<string> Generate(string dic, int length)
    {
        var result = new List<string>();
        unsafe
        {
            IntPtr p = Marshal.AllocHGlobal(sizeof(char));
            var seed = (char*)p.ToPointer();
            int i = 0;
            for (;i < length;i++)
            {
                *(seed + i) = dic[0];
            }
            *(seed + i) = '\0';

            bool tmp = true;
            while (tmp)
            {
                result.Add(new string(seed));
                tmp = FixedPointCombinator(
                    x =>
                    {
                        if (x != null)
                        {
                            return (s) =>
                            {
                                int len = 0;
                                for (;*(s.Seed + len) != '\0';len++) { }
                                if (s.Idx < 0 || s.Idx >= len)
                                    return false;

                                char c = s.Seed[s.Idx];
                                if (s.Dic.IndexOf(c) < s.Dic.Length - 1)
                                {
                                    c = s.Dic[s.Dic.IndexOf(c) + 1];
                                    *(s.Seed + s.Idx) = c;
                                    return true;
                                }
                                else
                                {
                                    c = s.Dic[0];
                                    *(s.Seed + s.Idx) = c;
                                    s.Idx--;
                                    return x(s);
                                }
                            };
                        }

                        return null;
                    })(new Args() { Seed = seed, Idx = length - 1, Dic = dic });
            }
        }

        return result;
    }

    private Func<Args, bool> FixedPointCombinator(
        Func<Func<Args, bool>, Func<Args, bool>> f1)
    {
        return (x) => f1(FixedPointCombinator(f1))(x);
    }

    public override string ToString()
    {
        return "Generate numbers(Fixed-Point Y, unsafe)";
    }

    private unsafe struct Args
    {
        public char* Seed;
        public int Idx;
        public string Dic;
    }
}

下面是运行结果：

结语

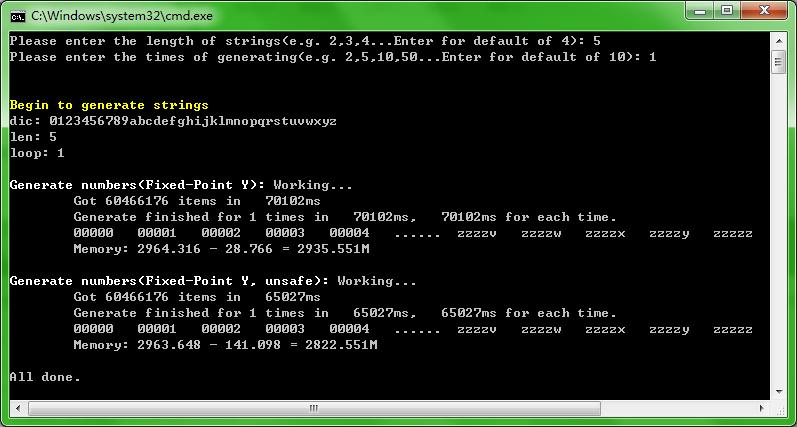
OK，我们来系统地比较一下这些方案吧，由于时间关系，我测试了生成字符串长度为4，并且每个方案在Release下运行50次取平均的结果：

值得注意的是，方案二的内存占用却异常的高，难道是因为Demo代码统计的问题？针对这个，我又重新运行了方案二和方案五，并且对调了他们的执行先后顺序。如下图：

方案 平均耗时（ms） 连续运行50次后的内存占用（M） 方案一：循环拼接字符串 1930 241.852 方案二：循环拼接字符串Unsafe版 813 1546.480 方案三：字符串模拟数字依次循环进行进制转换 2738 167.105 方案四：字符串模拟数字依次自增+1 1550 93.297 方案五：字符串模拟数字依次自增+1的Unsafe版 853 74.844 方案六：不动点组合子 2152 111.406 方案七：不动点组合子Unsafe版 1907 94.691

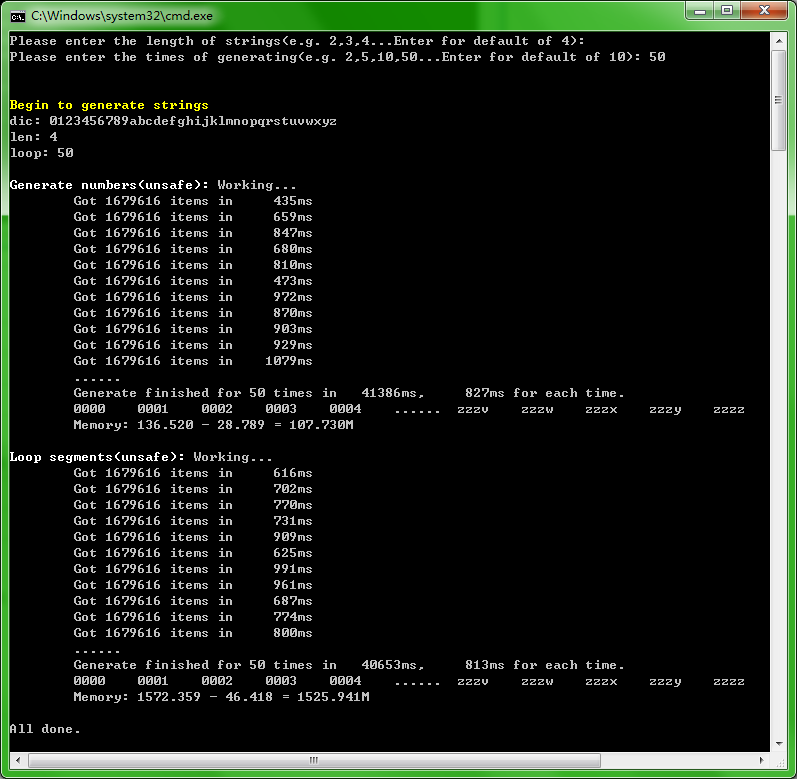
从上表中可以看出：

非字符串方案（四、五）比字符串方案（一、二）更优；
Unsafe版本比对应的原始版本更优，想必是Unsafe版本只处理上下文必要的相关逻辑，不用像Framework里那样考虑得面面俱到。

具体地：

时间消耗上，方案二和方案五不相上下，并且远低于其他方案，作为Unsafe升级版，也都差不多是原始版本的1/2；
内存消耗上，方案二的内存占用异常高，而同为Unsafe版本的方案五内存占用最低。

详细分析代码可以看出，方案二为了保证生成的字符串集合的顺序，因此在每一次递归时都构造了一个新的数组，并保留了原来数组（seed），而不像方案五那样，直接在每一次循环时修改指针所指变量的值。我猜想，如果将方案二中对数组的相关操作再次进行Unsafe化，比如不为扩容而另外构造新数组，而是直接将seed扩容，那内存的占用应当会降低很多。只是Array.Resize<T>并不支持 char*，得自己写一个了~

最后来看，整个七个方案中，莫过于方案五最优了：

它以数字自增的逻辑思路来执行，从而达到了O(1)的时间复杂度（虽然仍然用到了递归）；
没有使用 framework 中的 string，而是直接有针对性地使用 char*，从而有效避免了不必要的字符串级别操作。
没有使用像方案二中的数组，而是直接改写指针所指变量的值，从而有效避免了大量的内存分配，降低了内存的占用。

综上，以下为一些心得小记：

对字符串的操作比想象中降性能、耗内存资源。
要提高执行效率，使用非安全代码改写针对字符串的算法可以以空间换时间，有效地提供执行效率。（既然是非安全代码，还需全方位测试。不过请放心，它将不会导致引用该程序集的其他程序集启用非安全代码）
从递归改到Fixed-Point Y的过程是个很绕脑袋的过程，我确信这是一种很重要的思想（函数式、自生成），但仍然没能明确其更具体的应用场景，何时何地它是最优的解决方案？

上一篇： Java程序中解决数据库超时与死锁下一篇：中央纪委监察部网站正式开通网络反腐升级