骰子作画的算法_最新动态_新闻资讯_程序员俱乐部

　　程序员 Scott MacDonald 做了一个很有趣的项目----骰子作画。

　　他用黑底白点的骰子。

　　模拟出一张人像照片。

　　把图像放大，就可以看得更清楚。

　　他一共用了2500多颗骰子。

　　最后的成品就是这样。

　　任何一张图片都可以用骰子模拟出来，算法非常简单：将图片分成若干个区域，每个区域经过计算以后，用1-6之间的一个整数表示，代表骰子的一个面。这种将连续的量转化成不连续的整数的算法，属于 vector quantization（矢量量化）的一个应用。

　　具体来说，

　　第一步，将图片分割成16像素 x16 像素的小方块。

for (int i=0; i < (pic_width/16); ++i) {

for (int j=0; j < (pic_height/16); ++j) {

patch = cropped_img.get (i*16, j*16, 16, 16);

}

}

　　第二步，每个小方块内共有256个像素，将每个像素点的灰度值，存入一个数组。

for (int k=0; k < patch.pixels.length; ++k) {

x[k] = rgb2gray (patch.pixels[k]);

}

int rgb2gray (int argb) {

int _alpha = (argb >> 24) & 0xFF;

int _red = (argb >> 16) & 0xFF;

int _green = (argb >> 8 ) & 0xFF;

int _blue = (argb) & 0xFF;

return int (0.3*_red + 0.59*_green + 0.11*_blue);

}

　　第三步，计算该数组的平均值，并用1-6之间的一个整数来表示。

int dice_num = six_step_gray (mean (x));

int mean (int[] x) {

float m = 0;

for (int i=0; i < x.length; ++i) {

m += x[i];

}

m = m/x.length;

return int (m);

}

int six_step_gray (int x) {

if (0 <= x && x <= 41) return 1;

if (41 < x && x <= 83) return 2;

if (83 < x && x <= 124) return 3;

if (124 < x && x <= 165) return 4;

if (165 < x && x <= 206) return 5;

if (x < 206 && x <= 247) return 6;

else return 6;

}

　　整数1，表示骰子朝上的一面有1个白点；整数2，表示有2个白点；以此类推。白点越少，表示这个区域越接近全黑；白点越多，表示越接近全白。根据白点值，将骰子依次放入，就能模拟出全图。

　　这种算法早在1981年就有人提出，当时用的是1~9个白点的多米诺骨牌。

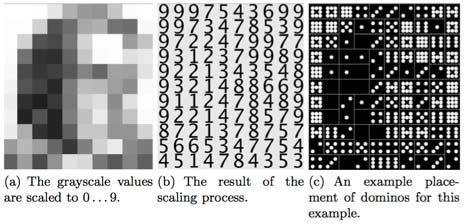
　　如果区域划分得越小，模拟图的生成效果就越好。

　　此外，不用编程，使用 Photoshop 也可以得到类似效果。