给出基本定义：
第一题：hdu 1054 Strategic Game
http://acm.hdu.edu.cn/showproblem.php?pid=1054
求：最小顶点覆盖 == 【最大匹配(双向建图)】/2
证明：最小顶点覆盖 == 最大匹配http://www.matrix67.com/blog/archives/116
第二题：hdu 1068 Girls and Boys
http://acm.hdu.edu.cn/showproblem.php?pid=1068
求：最大独立集 == |P| 减 【最大匹配(双向建图)】/2
由于只能是男女之间有关系，所以必然不存在奇圈【长度为奇数的环】
必然是二分图
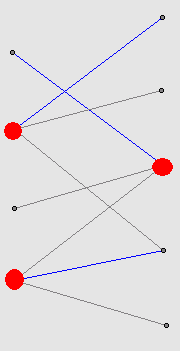如图红点为最小覆盖顶点，有3个，除了这三个点以外的点所组成的集合就是最大独立集，两两之间无任何关系
第三题：hdu 1150 Machine Schedule
http://acm.hdu.edu.cn/showproblem.php?pid=1150
求：最小顶点覆盖 == 最大匹配
第四题：hdu 1151 Air Raid
http://acm.hdu.edu.cn/showproblem.php?pid=1151
求：最小路径覆盖 == |P| 减 【最大匹配】，适用于有向无环图【DAG图】
有环不一定成立……
对于公式：最小路径覆盖=|P|－最大匹配数；
可以这么来理解：
如果匹配数为零，那么P中不存在有向边，于是显然有：
最小路径覆盖=|P|－最大匹配数=|P|－0=|P|；
即P的最小路径覆盖数为|P|；
P'中不在于匹配边时，路径覆盖数为|P|；
如果在P'中增加一条匹配边pi'－－>pj''，那么在图P的路径覆盖中就存在一条由pi连接pj的边，也就是说pi与pj 在一条路径上，于是路径覆盖数就可以减少一个；
如此继续增加匹配边，每增加一条，路径覆盖数就减少一条；
第五题：hdu 1281 棋盘游戏
http://acm.hdu.edu.cn/showproblem.php?pid=1281
①求在白色格子最多能放多少个车
放车的条件：
车与车之间不可同行或者同列
根据最大匹配的特性，每个匹配木有公共点，如果把行和列看成点进行最大匹配就可以求出既不同行也不同列的匹配个数maxs，也就是答案了
②求关键放车点的个数【也就是说这个点必须放上一个车才能达到最大匹配数】
思路：枚举可放点【其实就是可匹配的一条边】，让它无效化，然后再求出一个最大匹配tp，如果tp<maxs，说明这条边是关键，所以关键点+1
第六题：hdu 1498 50 years, 50 colors
http://acm.hdu.edu.cn/showproblem.php?pid=1498
爆破气球的条件：一次只能爆破一行或一列，选择一种颜色爆破，给你k次机会，输出不可能爆破完的气球的颜色
利用最大匹配的特性，行和列进行匹配，匹配条件是颜色相同，可以看成最小顶点覆盖，一个匹配边就把同一行或同一列的气球都爆破了
枚举所有颜色分别求出行和列的最大匹配maxs，那么这种颜色至少需要maxs次的爆破才可爆完，则如果 k < maxs 就不可能爆完咯
第七题：hdu 1528and1962 Card Game Cheater
http://acm.hdu.edu.cn/showproblem.php?pid=1528
http://acm.hdu.edu.cn/showproblem.php?pid=1962
给出两组牌，要你配对，求第二组牌赢得的最多分数，对应的牌大的得一分
跟田忌赛马类似
直接求最大匹配，匹配条件是第二组的牌大于第一组的牌
第八题：hdu 1507 Uncle Tom's Inherited Land*
http://acm.hdu.edu.cn/showproblem.php?pid=1507
格子间的匹配，求最大匹配，匹配条件是2个格子相邻，且2个格子都是陆地
给格子编号就可以套模板了【注意要双向建图】
第五题游戏棋盘代码：
#include <iostream>
#include <fstream>
#include <algorithm>
#include <string>
#include <set>
//#include <map>
#include <queue>
#include <utility>
#include <iomanip>
#include <stack>
#include <list>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
//#include <ctime>
#include <ctype.h>
using namespace std;
#define LL __int64
#define inf 0x3fffffff
#define M 105
struct pos{
int v;
int i;
};
vector<pos> g[M];
int match[M], n, key;
bool vis[M];
void init ()
{
int i;
for (i = 1; i <= n; i++)
g[i].clear();
}
bool dfs (int u) //dfs寻找增广路
{
int i, v;
for (i = 0; i < g[u].size(); i++) //v是二分图右边的元素
{
v = g[u][i].v;
if (g[u][i].i == key) //u-v这条边的编号是key的话无效
continue;
if (!vis[v])
{
vis[v] = true;
if (match[v] == 0 || dfs (match[v]))
{
match[v] = u;
return true;
}
}
}
return false;
}
int main()
{
int m, k, u, v, maxs, tp, imp, i, cc = 1;
pos x;
while (~scanf ("%d%d%d", &n, &m, &k))
{
init();
for (i = 1; i <= k; i++)
{
scanf ("%d%d", &u, &v);
x.v = v, x.i = i;
g[u].push_back (x); //u-v边的编号从1到k
}
maxs = imp = 0;
for (key = 0; key <= k; key++) //枚举要无效化的边编号
{
/**********一次匈牙利算法**********/
tp = 0;
memset (match, 0, sizeof(match)); //匹配对象
for (i = 1; i <= n; i++) //i是二分图左边的元素
{
memset (vis, false, sizeof(vis)); //访问标记
if (dfs (i)) //找到增广路匹配数+1
tp++;
}
/**********一次匈牙利算法**********/
if (maxs < tp)
maxs = tp;
if (tp < maxs) //删了key这条边就没法得到最大匹配，说明这条边是关键点
imp++;
}
printf ("Board %d have %d important blanks for %d chessmen.\n", cc++, imp, maxs);
}
return 0;
}
最后一题：Uncle Tom's Inherited Land*
#include <iostream>
#include <fstream>
#include <algorithm>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <utility>
#include <stack>
#include <list>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
//#include <ctime>
#include <ctype.h>
using namespace std;
#define L long long
#define inf 0x3fffffff
#define M 10005
bool vis[M], num[M];
int n, match[M], c;
bool dfs (int u) //由于是双向匹配，所以与u相邻的点都要尝试跟u匹配
{
int i;
i = u + 1;
if (i % c != 0)
{
if (!num[i] && !vis[i])
{
vis[i] = true;
if (match[i] == -1 || dfs (match[i]))
{
match[i] = u;
return true;
}
}
}
i = u + c;
if (i < n)
{
if (!num[i] && !vis[i])
{
vis[i] = true;
if (match[i] == -1 || dfs (match[i]))
{
match[i] = u;
return true;
}
}
}
i = u - 1;
if (i >= 0 && i % c != c - 1)
{
if (!num[i] && !vis[i])
{
vis[i] = true;
if (match[i] == -1 || dfs (match[i]))
{
match[i] = u;
return true;
}
}
}
i = u - c;
if (i >= 0)
{
if (!num[i] && !vis[i])
{
vis[i] = true;
if (match[i] == -1 || dfs (match[i]))
{
match[i] = u;
return true;
}
}
}
return false;
}
int main()
{
int r, m, x, y, maxs, tx, ty, i;
while (scanf ("%d%d", &r, &c), (r||c))
{
n = r * c;
scanf ("%d", &m);
memset (num, false, sizeof(num));
while (m--)
{
scanf ("%d%d", &x, &y);
num[(x-1)*c+y-1] = true; //坐标转化成编号
}
/****************一次匈牙利****************/
maxs = 0;
memset (match, -1, sizeof(match));
for (i = 0; i < n; i++)
{
if (num[i])
continue;
memset (vis, false, sizeof(vis));
if (dfs (i))
maxs++;
}
/****************一次匈牙利****************/
printf ("%d\n", maxs/2); //双向建图的结果
for (i = 0; i < n; i++)
{
if (!num[i] && match[i] > -1 && !num[match[i]])
{
//判断是否有匹配，并且判断是否已输出过
x = i / c; //编号变回坐标
y = i % c;
tx = match[i] / c;
ty = match[i] % c;
num[i] = num[match[i]] = true; //一个格子匹配后不可再次出现
printf ("(%d,%d)--(%d,%d)\n", x+1, y+1, tx+1, ty+1);
}
}
}
return 0;
}
- 大小: 3.8 KB
- 大小: 17.3 KB
- 大小: 163.1 KB
相关文章![[转]分享一个thinkphp提示页面代码](/Upload/SmallIMG/2012070921/F72EEFA831388BCD.jpg)
