????之前我们接触学习了Dijkstra算法求解一个顶点到其他各个顶点的最短路径和距离,但如果我们想知道每一对顶点的最短路径和距离时,可以通过以每一个顶点作为源点循环求出每对顶点之间的最小距离。除此之外,我们可以利用本篇博客即将学习的弗洛伊德(Floyd)算法来求两顶点之间的最短距离。
弗洛伊德(Floyd)算法
?
1)算法思想原理:
?
????? 从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
?
2).算法描述:
?
a.从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
?
b.对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
?
3)具体实现步骤
要操作的有向图如图所示:
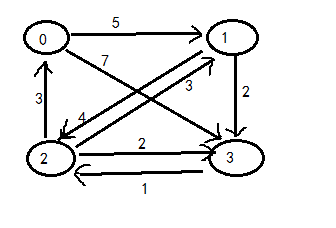
用邻接矩阵表示为:
?
class="cpp" name="code">#define INF 99999 //表示不可到达
#define MAXSIZE 4 //表示图的结点数
//邻接矩阵存储图的信息
int map[MAXSIZE][MAXSIZE]={
{0,5,INF,7},
{INF,0,4,2},
{3,3,0,2},
{INF,INF,1,0}
};
?
?
定义
A[MAXSIZE][MAXSIZE]:?? A[i][j]表示当前顶点i到j的最短距离
path[MAXSIZE][MAXSIZE]:?? 保存最短路径
?
Floyd算法过程矩阵的计算----十字交叉法
先初始化2个数组:
?
//数据初始化
for(int i=0;i<MAXSIZE;i++)
{
for(int j=0;j<MAXSIZE;j++)
{
A[i][j]=map[i][j];
path[i][j]=-1;//初始化为-1
}
}
?
?
即得到:

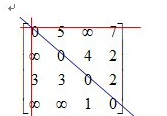
?1)使用十字交叉法,划去第0行和第0列以及左对角线,即
?
?
此时不在这三条线上的数据有:A[1][2]=4;A[1][3]=2;A[2][3]=2;A[2][1]=3等6个数。
此时根据Ak(i,j) = min(?Ak-1(i,j),?Ak-1(i,k) +?Ak-1(k,j) )对比看是否要数据更新
例如看A[2][1]=3这个数是否要更新。
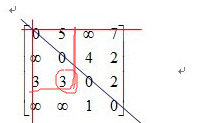
?
此时A[0][1]+A[2][0]=8>A[2][1]=3
所以不用更新,其他5和数都是这样判断,会发现都不用更新
?
?1)使用十字交叉法,划去第1行和第1列以及左对角线,即

?
此时不在这3条线上的数据依次是:A[0][2],A[0][3],A[2][0],A[2][3],A[3][0],A[3][2]
我们来看数据A[0][2]。

?
?
发现
A[0][2]>A[0][1]+A[1][2]=5+4=9(图中画出矩形顶点的和,即A[0][2]附近2个顶点的和,不是对角线那个顶点);
此时修改A[0][2]=9,path[0][2]=1(即划去的行号和列号,也是3条线交点的坐标)
按照此方法检查其他剩下的5个数,最后得到

?
以此类推。最后得到:
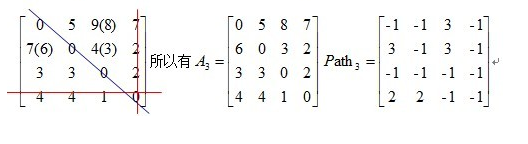
?
理解清楚步骤后,写出Floyd算法代码为:
?
//弗洛伊德算法
void Floyd()
{
int path[MAXSIZE][MAXSIZE];//保存最短路径
int A[MAXSIZE][MAXSIZE];//a[i][j]表示当前顶点i到j的最短距离
//数据初始化
for(int i=0;i<MAXSIZE;i++)
{
for(int j=0;j<MAXSIZE;j++)
{
A[i][j]=map[i][j];
path[i][j]=-1;//初始化为-1
}
}
for(int diagonal=0;diagonal<MAXSIZE;diagonal++)//左对角线
{
for(int k=0;k<MAXSIZE;k++)//行
{
if(k!=diagonal)//除去此行所有的点
for(int j=0;j<MAXSIZE;j++)//列
{
if(j!=diagonal)//除去此列所以的点
{
if(k!=j)//除去对角线的点
{
if(A[k][j]>A[diagonal][j]+A[k][diagonal])//满足条件
{
A[k][j]=A[diagonal][j]+A[k][diagonal];
path[k][j]=diagonal;
}
}
}
}
}
}
}
?
得到A[MAXSIZE][MAXSIZE]和path[]数组后。
A[i][j]:?表示从顶点i到顶点j的最短距离。
?
而最短路径还要通过path[]数组计算得来。计算方法如下:

?
例如我们求解顶点3到顶点1的最小距离和路径:
?
最小距离:A[3][1]=4
最短路径:
path[3][1]=2;
path[2][1]=-1(一旦值为-1,停止计算)
所以顶点1前面经过的是顶点2,
即最后路径为:
3->2->1;
j结果显示代码为:
//结果输出:
for(int i=0;i<MAXSIZE;i++)
{
for(int j=0;j<MAXSIZE;j++)
{
if(A[i][j]==INF)
cout<<"从顶点"<<i<<"到顶点"<<j<<"不存在路径"<<endl;
else
{
cout<<"从顶点"<<i<<"到顶点"<<j<<"最短距离为: "<<A[i][j]<<" 其路径为:";
vector<int>temp;
temp.insert(temp.begin(),j);//把终点插入
int ok1=i,ok2=j;
while(true)
{
ok1=path[ok1][ok2];
if(ok1==-1)
break;
temp.insert(temp.begin(),ok1);
}
temp.insert(temp.begin(),i);//把起点插入
for(int z=0;z<temp.size();z++)
cout<<temp[z]<<" ";
cout<<endl;
}
}
}
?
最终程序结果:
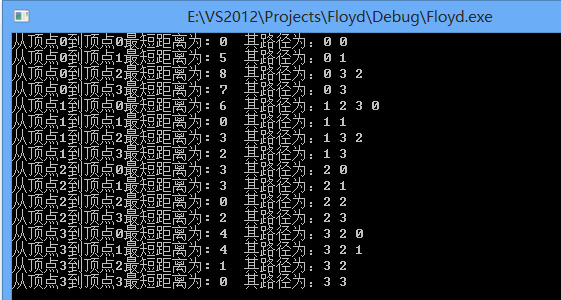
?
?附上源码地址:https://github.com/longpo/algorithm/tree/master/Floyd