最小生成树详解_C/C++_编程开发_程序员俱乐部

生成树和最小生成树有许多重要的应用。 例如：要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

下面开始最小生成树的学习。首先需要清楚一些概念。

?

生成树的定义:连通图G的一个子图如果是一棵包含G的所有顶点的树，则该子图称为G的生成树。 ??????????? ? 生成树是连通图的极小连通子图。

所谓极小是指：若在树中任意增加一条边，则将出现一个回路；若去掉一条边，将会使之变成

连通图。?

?

最小生成树的定义：带权图对应的生成树, 生成树各边的权值总和称为生成树的权。权最小的生

树称为最小生成树

?

明白了概念之后，就开始学习使用Prim算法（普里姆算法)来生成最小hashu.html" target="_blank">二叉树。

首先我们要生成最小二叉树的无向图如下所示：

?

?

?

当然，我们先要把这个无向图数据化，让计算机可以理解这个图，我们这次使用邻接矩阵来数据化此无向图

即用个二维数组表示：

class="cpp" name="code">#define INF 100000 //表示不可到达

#define MAXSIZE 6 //表示图的结点个数

//邻接矩阵存储图的信息
int map[MAXSIZE][MAXSIZE]={
	{0,4,2,3,INF,INF},
	{4,0,5,4,3,INF},
	{2,5,0,1,INF,2},
	{3,4,1,0,6,2},
	{INF,3,INF,6,0,4},
	{INF,INF,2,2,4,0}
};

?

?Prim()算法

?基本思想：假设G＝(V，E)是连通的，TE是G上最小生成树中边的集合。算法从U＝{u0}（u0∈V）、TE＝{}开始。重复执行下列操作：

???在所有u∈U，v∈V－U的边(u，v)∈E中找一条权值最小的边(u0,v0)并入集合TE中，同时v0并入U，直到V＝U为止。

???此时，TE中必有n-1条边，T=(V，TE)为G的最小生成树。

???Prim算法的核心:始终保持TE中的边集构成一棵生成树。

?

上面的基本思想看起来非常费解，为了更好的理解，我们一步步进行说明：

我们首先定义一个存储最小生成树的结构体：

?

//用来存储最小生成树的边和权值
struct path
{
	int start;//起点
	int end;  //终点
	int weight; //权值
};

?

?我们定义一个结构体path数组lowcost来存放候选边，此算法的难点就在lowcost数组的更新与选择。

path lowcost[MAXSIZE];//邻近点（未被标记）的最小距离

?

为了详细说明lowcost数组的更新与选择，我在画图上画出了步骤如下

?

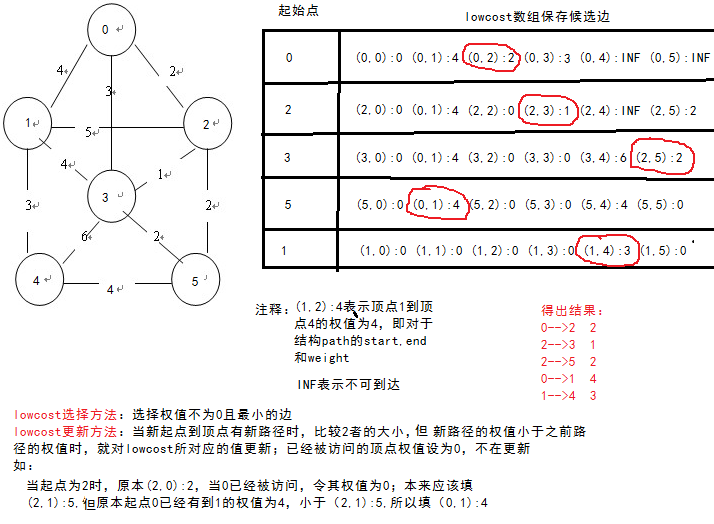
理解了图中的原理的话，那么Prim（）算法的代码就能写出来了，代码如下：

?

?

//普里姆算法--最小生成树
void Prim(path section[],int v)//v起始点
{
	path lowcost[MAXSIZE];//邻近点（未被标记）的最小距离

	path tree[MAXSIZE-1];  //存放最小生成树

	int visited[MAXSIZE]={0};  //已经访问的结点为1

	path min;

	for(int i=0;i<MAXSIZE;i++)
	{
		lowcost[i].weight=map[v][i];
		lowcost[i].start=v;	
		lowcost[i].end=i;
	}

	//循环查找路径，查找次数为结点数减1
	for(int j=0;j<MAXSIZE-1;j++)
	{
		//获取权值不为0且最小的边
		min.weight=INF;
		for(int i=0;i<MAXSIZE;i++)
		{
			
			if(lowcost[i].weight!=0&&lowcost[i].weight<min.weight)
			{
				min=lowcost[i];
			}
		}

		tree[j]=min;//获取最小权值，存入最小生成树数组里

		visited[v]=1;//已访问

		v=min.end;//修改起始点

		//修改lowcost数组
		for(int i=0;i<MAXSIZE;i++)
	    {
			//若新的权值小于之前的权值，则更改
			if(map[v][i]<lowcost[i].weight)
			{
				lowcost[i].weight=map[v][i];
				lowcost[i].start=v;
				lowcost[i].end=i;
			}

			//已经访问的结点为0
			if(visited[i]==1)
               lowcost[i].weight=0;

	    }

	}

	//输出生成的最小二叉树的结果
	for(int i=0;i<MAXSIZE-1;i++)
	{
		cout<<tree[i].start<<"->"<<tree[i].end<<"  "<<tree[i].weight<<"  "<<endl;
	}

}

?

至此，我们就完成了Prim（）算法的学习。

?

得到的最小生成树为：

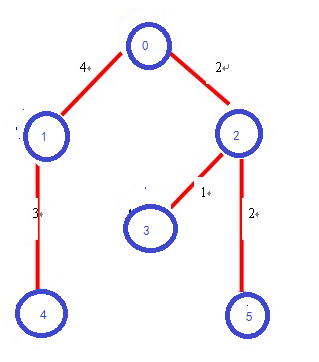
?附上源码地址：https://github.com/longpo/algorithm/tree/master/MakeTree