二叉树详解_C/C++_程序员俱乐部

您所在的位置：程序员俱乐部 > 编程开发 > C/C++ > 二叉树详解

二叉树详解

2015/3/25 21:16:36 hm4123660 程序员俱乐部我要评论(0)

摘要：树是一种比较重要的数据结构，尤其是二叉树。二叉树是一种特殊的树，在二叉树中每个节点最多有两个子节点，一般称为左子节点和右子节点（或左孩子和右孩子），并且二叉树的子树有左右之分，其次序不能任意颠倒。本篇博客将详细为大家解析二叉树。二叉树的链式存储结构是一类重要的数据结构，定义结果为：//定义树的结构structnode{node*lchild;node*rchild;stringdata;//初始化node(){lchild=rchild=NULL;}}
标签：详解二叉树

??????? 树是一种比较重要的数据结构，尤其是hashu.html" target="_blank">二叉树。二叉树是一种特殊的树，在二叉树中每个节点最多有两个子节点，一般称为左子节点和右子节点（或左孩子和右孩子），并且二叉树的子树有左右之分，其次序不能任意颠倒。本篇博客将详细为大家解析二叉树。

??????? 二叉树的链式存储结构是一类重要的数据结构，定义结果为：

class="cpp" name="code">//定义树的结构
struct node
{
	node * lchild;
	node * rchild;
	string data;
	//初始化
	node()
	{
		lchild=rchild=NULL;
	}
};

二叉树的建立

首先我们用户输入生成一棵二叉树，要生的的二叉树如下图所示：

#代表空结点。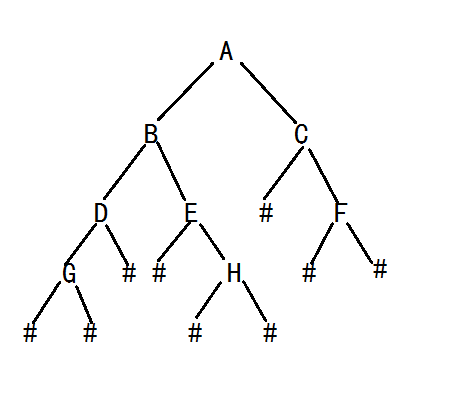

?下面我们根据上面图中所示的二叉树，利用先序依次输入ABDG###E#H##C#F##(即先序遍历）

生成二叉树的代码如下：

//二叉树生成--先序遍历输入要生成的二叉树数据，#代表空结点
void CreateTree(node * & root)
{
	 char data;
	 cin>>data;
	 if(data!='#')
	 {
		 root=new node;
		 root->data=data;
		 
		 CreateTree(root->lchild);
		
		 CreateTree(root->rchild);
		
	 }
}

二叉树节点查找

采用递归的方法在二叉树root里查找只为aim的结点，若找到此节点则返回其指针，否则返回NULL

查找代码如下：

//检查二叉树是否包含数据aim,有则返回其指针
node * Findnode(node * & root,string aim)
{
	node * p;
	if(root==NULL)//空树
		return NULL;
	else if(root->data==aim)
		return root;
	else
	{	
		p=Findnode(root->lchild,aim);
		if(p!=NULL)
			return p;
		else
			return Findnode(root->rchild,aim);	
	}
}

?这里解释一下递归中的return的意思：

return 对当前函数来说是结束了，对调用它的父函数来说你这个函数执行完成了，父函数就会接着执行下一语句。
没想到父函数马上又遇到一个return,父函数结束了，对爷爷函数来说父函数执行完成了，爷爷函数就接着执行下一个语句

二叉树遍历

1.先序遍历

先序遍历过程是：

1）访问根结点

2）先序遍历左子树

3）先序遍历右子树

先序遍历代码为：

void  PreOrder(node * root)//先序遍历
{
	if(root!=NULL)
	{
		cout<<root->data;
		PreOrder(root->lchild);
		PreOrder(root->rchild);
	}
}

2.中序遍历

中序遍历过程是：1）中序遍历左子树

2）访问根结点

3）中序遍历右子树

中序遍历的代码：

void  InOrder(node * root)//中序遍历
{
	if(root!=NULL)
	{
		
		InOrder(root->lchild);
		cout<<root->data;
		InOrder(root->rchild);
	}
}

3.后续遍历后序遍历过程是：

1）后序遍历左子树

2）后序遍历右子树3）访问根结点

后序遍历代码为：

void  PostOrder(node * root)//后序遍历
{
	if(root!=NULL)
	{
		
		PostOrder(root->lchild);
		PostOrder(root->rchild);
		cout<<root->data;
	}
}

二叉树高度计算

递归解法：
（1）如果二叉树为空，二叉树的深度为0
（2）如果二叉树不为空，二叉树的深度 = max(左子树深度，右子树深度) + 1

代码如下：

int NodeHeight(node * root)//计算二叉树高度
{
	int lchild,rchlid;
	if(root==NULL)
		return 0;
	else
	{
		lchild=NodeHeight(root->lchild);
		rchlid=NodeHeight(root->rchild);
		return (lchild>rchlid)?(lchild+1):(rchlid+1);
	}
}

输出二叉树叶子节点

递归解法：
参考代码如下：

void Showleaf(node * root)
{
	if(root!=NULL)
	{
		if(root->lchild==NULL&&root->rchild==NULL)
			cout<<root->data;
		Showleaf(root->lchild);//输出左子树叶子节点
		Showleaf(root->rchild);//输出右子树叶子节点
	}
}

运行结果为：