众所周知,三角形当中的任意两边之和始终大于第三边。在四边形中,我们还有类似的结论吗? 2015 年 2 月的 UyHiP 谜题就是:证明或推翻,四边形的三条最长边之和始终大于两条对角线的长度之和。
这个结论是正确的。下面的证明是由 Daniel Bitin 给出的。
首先,让我们先来证明一个引理:若 △ABC 中, ∠C ≥ 90° ,则 AB + CH > AC + BC ,其中 CH 是 AB 边上的高。不妨先来考虑 ∠C = 90° 的情况。
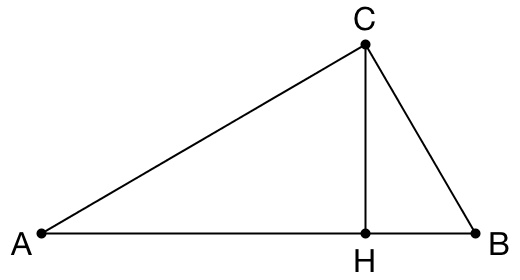
由勾股定理可知:
AB2 = AC2 + BC2
另外,由于这个三角形的面积有两种不同的计算方法,于是我们有:
AB · CH = AC · BC
前一个式子加上后一个式子的两倍,于是得到:
AB2 + 2 · AB · CH = AC2 + 2 · AC · BC + BC2
所以说
AB2 + 2 · AB · CH + CH2 > AC2 + 2 · AC · BC + BC2
即
(AB + CH)2 > (AC + BC)2
因此
AB + CH > AC + BC
如果 ∠C > 90° 呢?我们可以在 AB 边上找一个点 B′ ,使得 ∠ACB′ = 90° 。
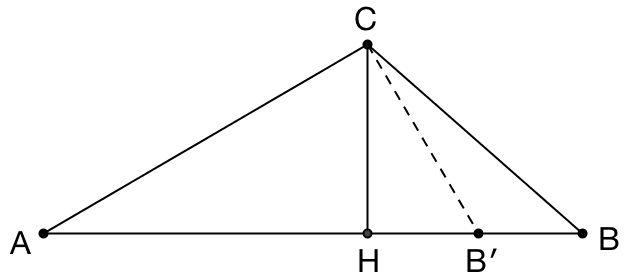
我们已经证明了
AB′ + CH > AC + B′C
而由于三角形两边之和大于第三边,我们有
BB′ + B′C > BC
两个不等式相加,于是得到
AB′ + CH + BB′ + B′C > AC + B′C + BC
即
AB + CH > AC + BC
引理也就证到了。
接下来就让我们来证明,在四边形 ABCD 中,三条最长边之和始终大于两条对角线的长度之和。
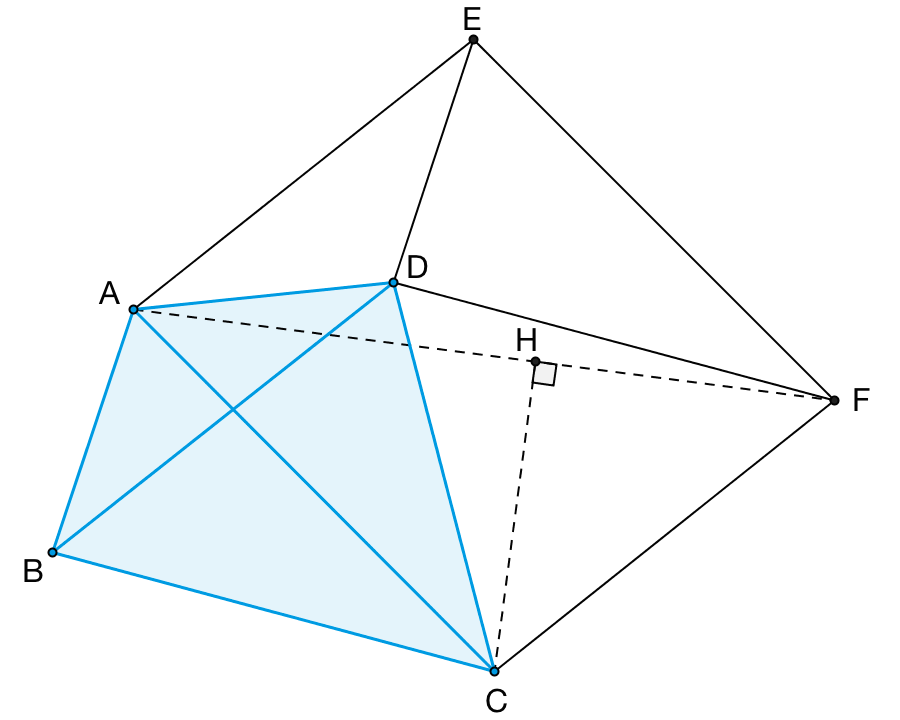
作平行四边形 ABDE 和 BCFD 。由于四边形 ABDE 是平行四边形,因而 AE 和 BD 是平行且相等的;由于四边形 BCFD 是平行四边形,因而 BD 和 CF 也是平行且相等的。因此, AE 和 CF 也就是平行且相等的了。这说明,四边形 ACFE 也是一个平行四边形。
注意,在平行四边形 ACFE 中, D 点到各个顶点的距离正好分别等于四边形 ABCD 的四边之长,并且 AE 和 CF 的长度都等于 BD , EF 的长度则等于 AC 。为了证明本文最开头的结论,我们只需要说明,在 DA 、 DC 、 DF 和 DE 中,其中三条边的长度之和大于平行四边形 ACFE 的两条邻边之和。由于这个平行四边形的两组对角分别相等,因而其中一组对角必然都是大于等于 90° 的,比如例图中的 ∠AEF 和 ∠ACF 。连接 AF 后,这个四边形就会被分割成两个直角三角形或者两个钝角三角形。在这两个三角形中,找出那个不含 D 点的三角形(如果 D 点在 AF 上,则随便选取一个三角形),比如例图中的 △ACF ,并作出该三角形 AF 边上的高 CH 。根据引理可得:
AF + CH > AC + FC
由于 △ADF 中两边之和大于第三边,因此 AD + DF > AF ;由于 H 点已经是线段 AF 上距离 C 点最近的点了,而 D 点还在线段 AF 的另一侧,因此 CD > CH 。所以,我们有
AD + DF + CD > AF + CH > AC + FC
即原四边形 ABCD 中,其中三条边的长度之和大于两条对角线的长度之和。