张承民/文
弯曲时空的引入
爱因斯坦在 1905 年创立以四维时空变换为基础的运动学,即狭义相对论(SR)。在爱因斯坦之前的时空观认为,相互运动的两个观测者彼此使用同一个钟, 因此时间表述相同。 然而, 这个隐喻的“同时”观念在考虑高速运动时遇到问题, 这是由于观测信号的速度是光速c,即每秒 30 万公里,当我们运动速度接近光速时,就必须考虑两者信号速度导致的时间偏差。日常生活中,我们的速度远远小于光速,比如车速 100 公里/小时,这只是光速的千万分之一,不足为虑。地球卫星的轨道速度如 10 公里/秒,这是光速的十万分之三, 因此轨道卫星的 GPS 计时系统在长期运行时要考虑相对论效应。 以上就是四维时空引入的理由,那就是参考系统彼此联络信号光速的考虑。 这里光线运动和自由粒子仍然是直线,所以时空是平直的。
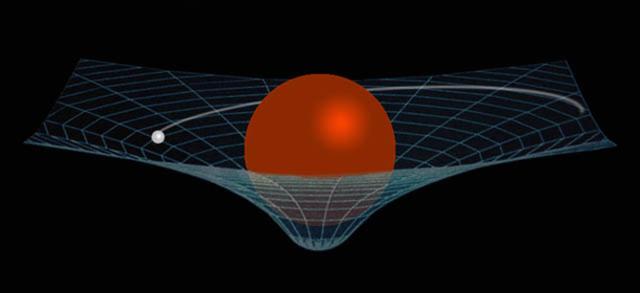
随后爱因斯坦便开始考虑在引力场中的运动描述,而星体万有引力将带来加速运动,这将与匀速运动的狭义相对论时空变换完全不同, 那里的观测者彼此匀速运动。 直到 1915 年, 在数学家格罗斯曼和希尔伯特的帮助下, 整合了狭义相对论和牛顿万有引力定律于一体,将引力场“力”的概念描述描述成时空弯曲, 即光线在引力场运动走测地线,这好比地球表面的大圆。在地面,我们的经验告诉自己走路是直线,假如你的路延长 20 公里,可能会发现你自己的路向下弯曲了,因为地球是圆的。这在欧洲地中海航海史上, 人们发现远方的船是慢慢地逐步跳下我们的视线, 这说明大海水面在大尺度是球面。但是在小范围,球面近视看成平面没有问题。同样的道理,在小的区域,引力造成的时空弯曲不明显,所以平直时空是完美近似。当引力场较强,观测区域变大时,弯曲的效应就得考虑,否则误差太大。举例类比,在北京市区旅行,你不要考虑地面弯曲问题;但是北京到海南岛的大尺度旅行,纬度引起的地面弯曲就值得考虑了。 所以在引力场下,狭义相对论(SR)+牛顿引力理论,变成了广义相对论(GR)。 当引力场极其微弱时,GR 回归 SR; 当运动速度较慢时,GR 回到牛顿引力理论。 因此广义相对论是以往理论成就的登峰造极,它不违反传统的低速弱引力的实验事实。 换言之, 狭义相对论和牛顿引力定律仅仅是爱因斯坦广义相对论的近似情况。 那么,广义相对论的独特新结论和预言将是什么情况? 炮弹在引力场下走抛物线,这是引力场造成的,即弯曲时空轨道运动的表现。如果没有引力场,或者沿着地心径向运动,那么炮弹走直线了。显然,牛顿苹果的下落属于后者的地心指向运动情况。
就此, 爱因斯坦广义相对论提出了三个可以验证的实验,并在其后由天文学家和物理学家实现了验证。这就是引力红移,光线偏折和水星近日点进动。后来又增加了第四个验证,即雷达回波的时间延迟。
引力红移
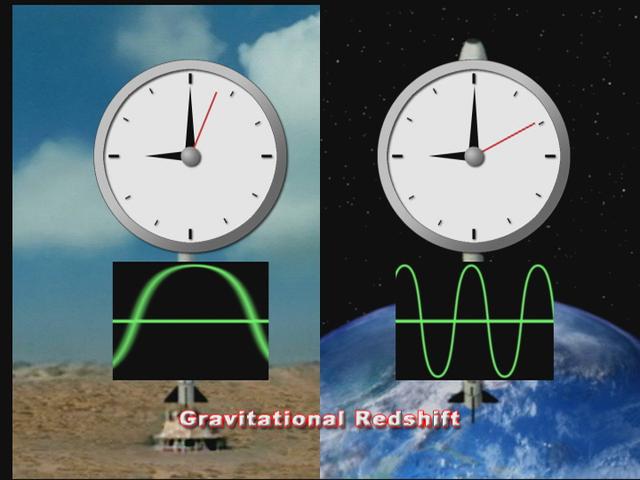
广义相对论认为,引力势强的地方,固有时间的流逝速度慢,也就是说离天体越近,时间越慢。这样,天体表面原子发出的光周期变长,由于光速不变,相应的频率变小,就会向光谱中红光方向移动,称为引力红移。宇宙中有很多致密的天体,可以测量它们发出的光的频率,并与地球的相应原子发出的光作比较,发现红移量与相对论预言一致。上世纪 60 年代初, 物理学家在地球引力场中利用伽玛射线的无反冲共振吸收效应(穆斯堡尔效应)测量了光垂直传播产生的红移,结果与广义相对论预言一致。
引力场中的光线偏折
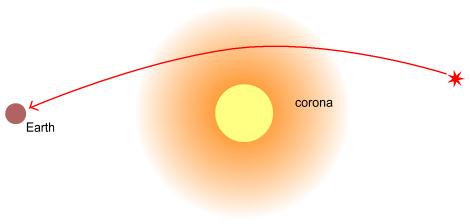
按照光的波动说,光在引力场中不应该有任何偏折,按半经典式的"量子论加牛顿引力论"的混合概念,用普朗克公式E=hv 和质能公式E=Mc^2 求出光子的质量,再用牛顿万有引力定律计算得到太阳附近的光的偏折角,是约 0.87 角秒。 而由广义相对论计算得到的偏折角是 1.75 角秒,为前者的两倍。1919 年,一战刚结束,英国科学家爱丁顿领导的两支考察队,利用跨大西洋日全食的机会观测,得到的结果约为 1.7 角秒,而且刚好在相对论实验误差范围之内,引起误差的主要原因可能是太阳大气对光线的偏折。在现代,通过射电望远镜可以观测类星体的射电信号在太阳引力场中的偏折,而不必等待日全食这种稀有的机会。高精度的测量结果进一步证实了广义相对论的结论。 进一步,当星体光源发出的光在引力场(星系及黑洞)附近经过时,光线会像通过透镜一样发生弯曲,当光路经过引力场不同位置时, 这导致地面观测者看到若干个星体的成像, 此类引力透镜现象极其普遍地被天文学家观测到。
水星近日点进动

天文观测记录了水星近日点(椭圆轨道短轴位置)每百年移动 5600 角秒,研究者曾经考虑了各种因素,根据牛顿理论只能解释其中的 5557 角秒,剩余的 43 角秒不知从何而来,无法解释。广义相对论的计算结果与平方反比的万有引力定律有所差异,这一差异刚好使水星的近日点每百年移动 43 角秒。
雷达回波时间延迟
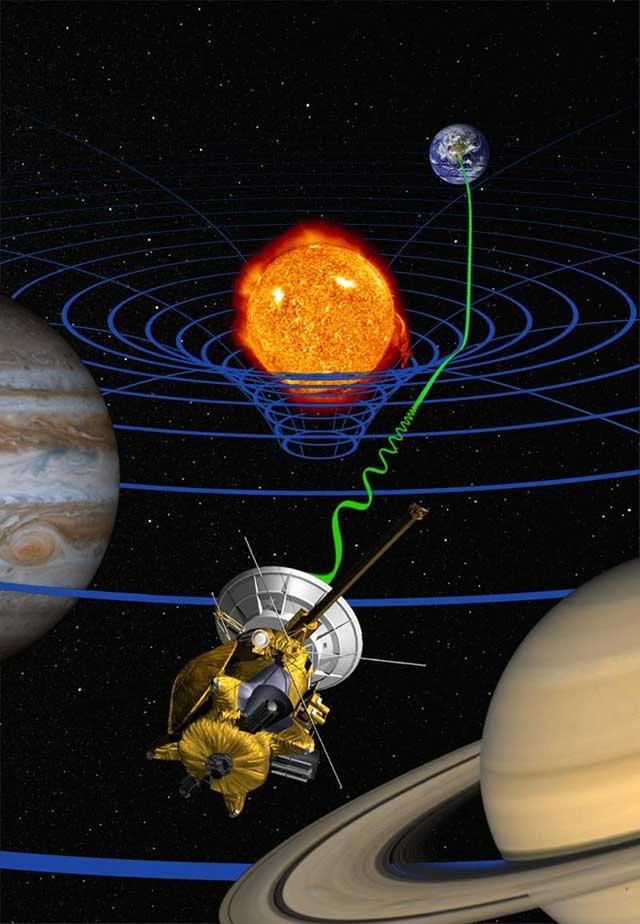
广义相对论认为光子靠近引力场时,就会发生时间延迟效应。光线轨迹在引力场中弯曲, 使得其路径延长。这种的弯曲现象可以等价地看成是一种折射,相当于有效光速减慢,因此从空间某一点发出的信号,如果途经太阳附近,到达地球的时间将有所延迟。这一想法首先由美国物理学家夏比洛(Shapiro)于 1964 年提出,由此来检验广义相对论是否正确。 从地球向行星发射雷达信号,接收行星反射的信号,测量信号往返的时间。 如果太阳正好处于行星和地球的连线,那么信号往返时间较没有太阳的情况变长。如此,可以检验空间是否发生了弯曲,是否有时间延迟。 1960 年代美国物理学家克服重重困难,完成了有关实验。 研究小组先后对水星、金星与火星进行了雷达实验,证明雷达回波确有延迟现象,太阳质量导致的雷达波往返的时间延迟将达到 200 毫秒左右, 结果与广义相对论预言相符。 近年研究人员试验月球作为反射靶,实验精度有所改善, 所得结果与广义相对论理论值一致。
2003 年天文学家利用卡西尼号土星探测器, 重复先前的实验, 测量精度在 0.002% 范围内观测与理论一致,这是迄今为止精度最高的广义相对论实验验证。此外,在毫秒脉冲星双星系统的计时观测中,来自星体的脉冲信号到达地球的时间存在延迟,这与广义相对论引力时间延迟的影响一致。(作者系中国国家天文台研究员)