一 一个问题

    在StackOverflow上有这么一个问题 Why is processing a sorted array faster than an unsorted array? 。例子中，对一个数组进行条件求和，在排序前和排序后，性能有很大的差别。原始的例子是C++和Java的，这里将其换成了C# ：

class="code">static void Main(string[] args)
{
    // Generate data
    int arraySize;
    int[] data;
    Random rnd;

    arraySize = 32768;
    data = new int[arraySize];

    rnd = new Random(0);
    for (int c = 0; c < arraySize; ++c)
        data[c] = rnd.Next(256);

    // Test
    long sum = 0;
    CodeTimer.Time("unsorted array", 100000, () =>
    {
        for (int c = 0; c < arraySize; ++c)
        {
            if (data[c] >= 128)
                sum += data[c];
        }
    });

    Array.Sort(data);

    sum = 0;
    CodeTimer.Time("sorted array", 100000, () =>
    {
        for (int c = 0; c < arraySize; ++c)
        {
            if (data[c] >= 128)
                sum += data[c];
        }
    });
    Console.ReadKey();
}

    代码中首先初始化了一个 32768大小的int型数组，给这个数组的每个元素随机赋予0-256之间的值，然后对该数组中大于128部分的数据进行求和，并将这个过程累加100000次。然后分别测量数组在排序前和排序后的 耗时。 这里使用了老赵的CodeTimer工具来，本人机器Xeon® E3-1230 v3@3.30GHz，在debug条件下，结果如下：

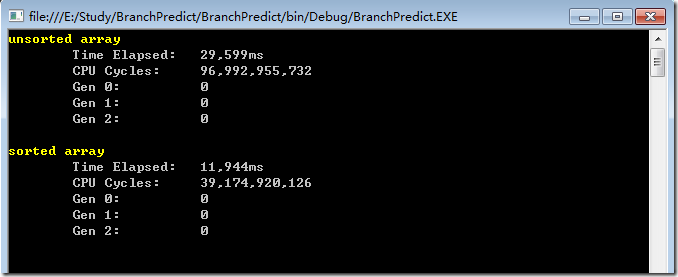
在release条件下，结果如下：

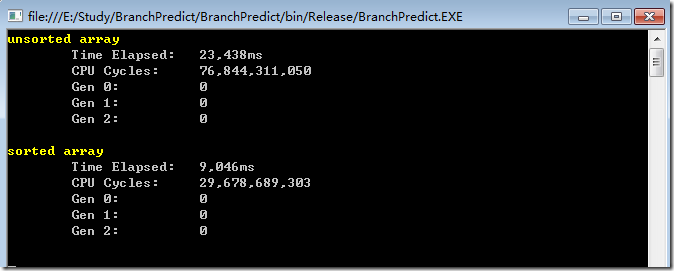
    然后作者提出了问题，为什么仅仅对数据进行了排序，处理速度就快了将近一倍还要多呢？

排名第一的回答，解释到是由于分支预测错误导致的性能惩罚，所以会产生性能的差别。要解释分支预测的惩罚，首先来看什么是分支预测，以及为什么预测错误会导致惩罚。

二 分支预测

    什么是分支预测? 直接说计算机概念或许不太好理解，答案以一个铁路分支路口的例子来说明了什么是分支预测。

考虑下面的铁轨分支:

    假设在还没有远距离信号通讯的时代。你是一个铁路分支路口的操作人员，当听到火车要来了，你根本不知道即将到来的这辆火车要开往哪个方向。于是，你让这辆或者停下来，问列车长这辆车要开往那个方向，然后将铁轨扳到对应的方向上。

   火车是一个很笨重的东西，因此具有很大的惯性，需要花很多时间启动和停止。

那么，有没有更好的办法呢？那就是，由你来猜这辆火车要往那个方向走！

• 如果猜对了，火车可以直接开往要去的方向
• 如果猜错了，火车要停下来，然后倒车，然后将车轨扳到正确的方向，然后火车重新开往正确的方向。

如果你的猜测总是正确的，那么火车就不用停下来了

如果你经常猜错，那么火车就要花很多的时间停下来，后退，然后重新开动。

现在，考虑一个if语句。if 语句编译为一个分支判断指令：

    如果你是处理器，你看到了这个分支，你事先完全没没有办法知道将从那个分支走。那么怎么办呢？你可以让指令暂停，等待直到之前的指令执行完成，然后比较结果，然后往正确的那个方向走。

   现代处理器很复杂，并且有很长的流水线，因此如果是这样的话，就需要很多时间来预热启动和停止。

那么，有没有更好一点儿的办法呢？你来猜这个指令将往那个方向走:

• 如果猜对了，语句可以继续执行
• 如果猜错了，处理器会放弃整个流水线，然后回退到分支地方，继续朝正确的分支执行。

如果每次都猜对，那么处理器不需要暂停可以一直执行

如果经常猜错，那么处理器就要话很多时间来暂停，回退，然后重新启动。

    这就是分支预测，虽然用火车铁轨的方式来解释可能不太恰当，因为通过旗帜或者信号可以提前通知要往那个方向。 但是对于计算机来说，处理器提前是不知道将要执行那个分支的，只有等到执行到分支判断的那一刻，值求出来之后才可以确定。

    因此如何采用一种策略来减少出错的次数，减少类似火车停车，倒车，再启动的问题呢？很自然的，可以根据以往的情形来推断！如果这个火车以前有99%的情况走左边，那么就可以在火车来之前猜测他走左边。如果行为发生变化，可以做相应的调整。如果发现每3次调整一次方向，那么总结出这个规律后就可以做出适当的调整。

    换句话说，我们需要总结出一些模式，然后遵循。这或多或少就是分支预测器的工作。

    大多数的应用都有行为良好的分支。因此现代的分支预测器能到达到90%以上的预测正确率。但是面对一些不可预见的分支和不可知的模式，分支预测器就没有多大用了。

通过上面的描述，出现性能差别的问题关键在于这个if语句：

if (data[c] >= 128)
    sum += data[c];

    注意到data这个数组里面的值是平均分布于0-255之间的。当数据排好序之后，前半部分的数据都会小于128，所以不会进到if语句里面，后半部分的值都大于128，所以会进到循环语句。

    这种规律对于分支预测器非常友好，因为分支判断语句发现总是选择某个方向很多次，于是就很容易做出判断。即使一个简单的计数器就可以正确预测分支的方向，除了改变方向之后的一两次预测失败之外。

   下面描述了理器在分支预测时的行为：

T = 该分支被选中
N = 该分支没有被选择

data[] = 0, 1, 2, 3, 4, ... 126, 127, 128, 129, 130, ... 250, 251, 252, ...
branch = N  N  N  N  N  ...   N    N    T    T    T  ...   T    T    T  ...

       = NNNNNNNNNNNN ... NNNNNNNTTTTTTTTT ... TTTTTTTTTT  (很容易进行预测)

   可以看到，当数据排好序之后，对分支预测器十分友好，很容易进行预测。

   但是，当数据完全是随机的时候，分支预测器便失去了用处，因为他无法预测随机的数据。因此会有大概50%的预测失败率。

data[] = 226, 185, 125, 158, 198, 144, 217, 79, 202, 118,  14, 150, 177, 182, 133, ...
branch =   T,   T,   N,   T,   T,   T,   T,  N,   T,   N,   N,   T,   T,   T,   N  ...

       = TTNTTTTNTNNTTTN ...   (基本上随机出现 – 很难预测)

那么怎么办呢？

   如果计算机没有办法将分支优化成条件转移，也可以使用一些技巧，牺牲一些可读性，移除条件判断，来提高性能

  比如，可以将下面的分支语句：

if (data[c] >= 128)
    sum += data[c];

替换为：

int t = (data[c] - 128) >> 31;
sum += ~t & data[c];

   这里使用了位运算，移除了分支预测。 移除分之后，再进行测试，在release条件下，结果如下：

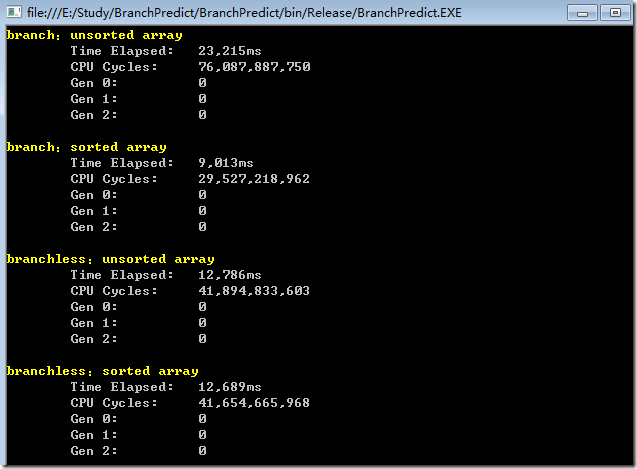
    可以看到，在没有分支判断的条件下，对有序和无序数组的处理，在速度上是差不多的。

    但是，为什么分支预测能够提高应用程序的执行效率，这就要来看看现代CPU的流水线设计了。

三 指令的流水线

    指令的流水线化(pipelining)是一种增加指令吞吐量(throughput)的方法，即在单位时间内能够提高同时执行指令的个数。他将一个基本的流水线拆分为了几个连续的，独立的步骤，然后某些步骤就可以同时执行。

    流水线化通过同时执行一系列操作增加了吞吐量，但是她并没有减少延迟，即并没有减少一条指令从执行开始到执行结束的时间，仍要等到这一系列指令完成。实际上,流水线化由于将一条指令拆分成了几个步骤从而可能会增加延迟。

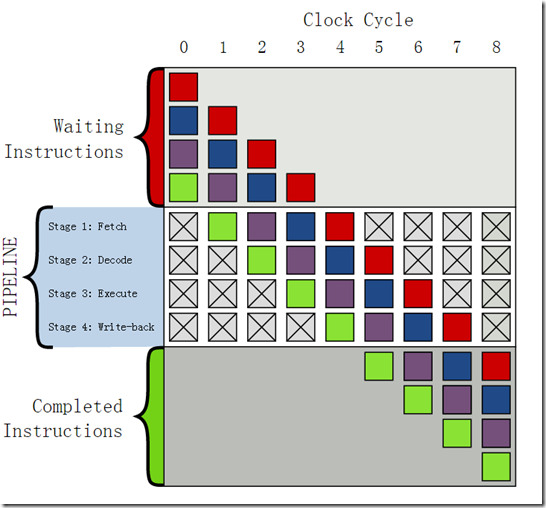
上图是一个具有4层流水线的示意图，一般的一个方法可以分为四个步骤，读取指令(Fetch)，指令解码(Decode),运行指令(Execute)和写回运行结果(Write back)。

上方灰色部分是一连串未运行的指令；下方灰色部分是已执行完成的指令，中间白色部分是流水线。下面是在每个时钟周期下指令的执行状态。

时钟序列

运行情况

0

四条指令等待运行

1

· 从存储器(memory)中读取绿色指令

2

· 绿色指令被解码

· 从主存储器中读取紫色指令

3

· 绿色指令被运行（事实上运算已经开始(performed)）

· 紫色指令被解码

· 从主存储器中读取蓝色指令

4

· 绿色指令的运算结果被写回到寄存器(register)或者主存储器

· 紫色指令被运行

· 蓝色指令被解码

· 从主存储器中读取红色指令

5

· 绿色指令被运行完毕

· 紫色指令的运算结果被写回到寄存器或者主存储器

· 蓝色指令被运行

· 红色指令被解码

6

· 紫色指令被运行完毕

· 蓝色指令的运算结果被写回到寄存器或者主存储器

· 红色指令被运行

7

· 蓝色指令被运行完毕

· 红色指令的运算结果被写回到寄存器或者主存储器

8

· 红色指令被运行完毕

    可见，流水线技术的主要目的就是通过重叠连续指令的步骤来提高吞吐量从而获得性能，要做到这一点，就必须能够实现确定要执行指令的序列和先后顺序，这样才能使流水线中充满了待执行的指令。当处理器遇到分支条件跳转时，通常不能确定执行那个分支，因此处理器采用分支预测器来猜测每条跳转指令是否会执行。如果猜测比较可靠，那么流水线中就会充满指令。但是，如果对跳转的指令猜测错误，那么就要要求处理器丢掉它这个跳转指令后的所有已做的操作，然后再开始用从正确位置处起始的指令去填充流水线，可以看到这种预测错误会导致很严重的性能惩罚，会导致大约20-40个时钟周期的浪费，从而导致性能的严重下降。

    在这部分开始处已经说明，如果编译器不能将分支跳转优化为条件转移指令，可以使用一些技巧，比如位运算来移除分支判断。

    那就是说，如果能够优化为条件转移指令，也能提升性能。在该问题的Update部分，提问者说:

    “GCC 4.6.1 with -O3 or -ftree-vectorize on x64 is able to generate a conditional move. So there is no difference between the sorted and unsorted data - both are fast. ”

    GCC是C/C++编译器，-O3是表示优化级别，可以将条件跳转优化为条件传送指令，从而使得在有序和无序情况下，对数据的处理同样高效，那么条件转移指令是什么呢？

四 条件传送指令

    关于条件传送指令，在CSAPP这本书的第3.6.6部分有教详细的介绍。这里针对这一具体问题详细介绍一下，条件转移指令是如何优化条件分支判断，从而利用流水线从而提高应用程序效率的。

    条件传送是一种条件跳转的一种替换策略，他首先就计算出一个条件的两种结果，然后等到执行到分支判断的地方，根据条件选择一个结果。只有在一些受限的条件下这种策略才可行，比如这个例子中的判断数字是否大于128然后求和。但是如果可行，就可以通过一条简单的条件传送指令来实现，而不是需要条件跳转指令来实现分支判断。比如下面的求两个数相减绝对值的方法，如果不使用条件传送指令：

    在比较大小之后，通过跳转指令，可以跳转到正确的分支然后执行接下来的逻辑。 要利用流水线技术，分支预测器不能依赖上一步骤的结果出来了再去做判断，它不可能等到cmpl执行完成再去选择分支，它需要提前做出判断，如果判断正确，没有问题，如果错误，就有比较严重的错误惩罚，从而影响应用程序性能。

    但是，如果使用条件跳转，情况如下：

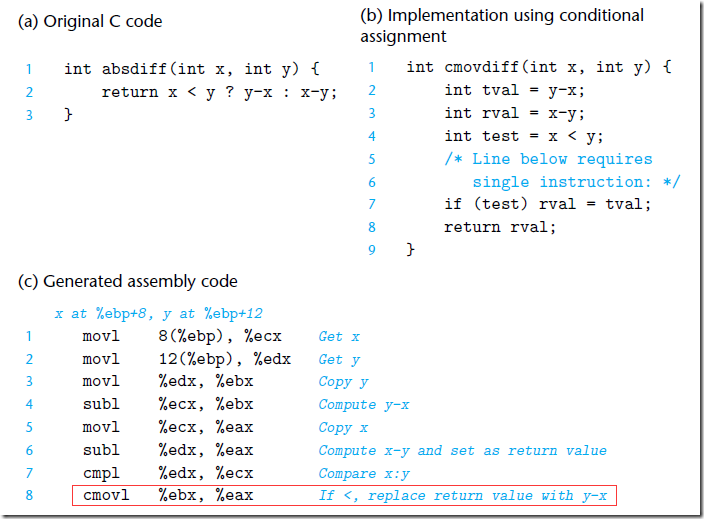
    首先计算出了两个分支的结果，然后判断条件，对两个分支的结果做出选择。这里面就没有分支判断和跳转指令，通过一条cmovl指令 (c表示条件，l表示less)就可以完成判断和赋值，这样分支预测器不需要做出分支判断，能够利用流水线，从而提高应用程序性能。

    但是，使用条件传送也不总是能够提高代码效率。如果条件的两个分支都需要大量的计算，那么实现计算出来就需要很多时间，当条件不满足时，这部分工作就浪费了。编译器必须在条件传送浪费的计算时间和分支预测错误造成的性能处罚之间做出权衡。一般的，只有在分支处的两个表达式都很容易计算时，比如只有一条加法指令，就像本例中的”

sum += data[c]; “ 这样，条件传送替换条件跳转才能提高效率。总的来说，条件数据传送提供了一种用条件转移来实现条件操作的替换策略，他只能用于一些很简单的场景，但是这种情况还是比较常见的，它能够充分利用现代处理器的流水线从而提高效率。

五 结论

    本文首先引用了StackOverflow上的一个问题及其解答说明了分支预测错误对应于程序性能的影响，然后简单分析了现代处理器流水线中如何使用分支预测提高应用程序性能以及分支预测错误导致的性能惩罚，最后结合问题给出的使用技巧替换分支判断，简要分析了为什么通过将条件跳转优化为条件传送能够充分利用指令流水线，从而同样能够提高程序性能。

    希望本文对您了解分支预测、条件转移和指令流水线有所帮助。

参考资料

1. Why is processing a sorted array faster than an unsorted array?
2. Computer systems.html" target="_blank">Systems: A Programmer's Perspective (2nd Edition),Chapter 3.66
3. Branch_predictor
4. Instruction_pipeline
5. why-is-a-conditional-move-not-vulnerable-for-branch-prediction-failure