薪资至少10K的一道题，你能拿下吗_.NET_编程开发_程序员俱乐部

我所了解的华为：

　　应届本科生8k+

　　应届硕士生10k+

　　应届博士生12k+

　　看到后什么感想？有没有只恨生不逢时运不佳的感觉？

　　很多人做3年多甚至更久，才能达到这个薪资水平，还不如一个新生。

　　在我看来，2013年应届生应该在4k~5k，今年应届生应该在5k~6k，如果达不到，自身找原因。对于一个慎重的人，应该慎重的选择你们的衣食父母，选择影响命运。

就扯这么多，好好选择。

 

---

　　以下这道题是今年5月份左右华为的朋友拿来做的（也是闲的无聊，想看看他们那边都有什么玩意可以耍耍）属于华为三级考题，内部使用，相对来说，这道题难度不高，应届生应该就有这个能力，不过审题一定要仔细了，不要因为当初审题不清，需求不明，后来做大量的修改。最忌讳的一点：不清不楚做开发，创造出来都是渣。

　　这道题大概用了一天时间，说实话，算法很简单，时间用的太长了，也真够渣渣了；

　　相关的地铁线和站，请去官方网站使用正则匹配获取，当初是这么干的，别手打，15线279站（不计算重复），累也累死了。

题中给了详细思路

 

---

 

背景概述

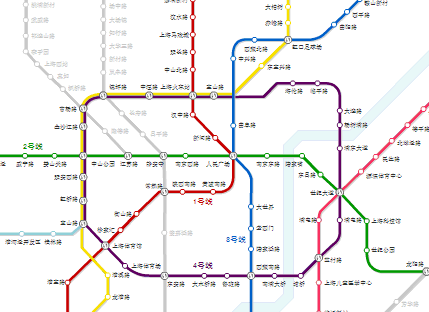
城市的地铁网络由多条线路组成

　　每条线路上有多个车站，线路自身没有交叉点

　　线路间交叉或重叠时，共用车站，在这些车站上可相互换乘

　　每条线路都是双向行车 线路有两种：

　　　　I形线和O形线 I形线有两个端点，乘客在端点处只能乘坐开往另外一端的地铁，在非端点处则有两个方向可选择。（如图中8号线）

　　　　O形线所有车站形成环，没有端点，乘客在任一站都有两个方向可选择。（如图中4号线）

 

 功能需求

　　在地铁网络中任选一站为起点，任选另一站为终点，中途可换乘，要求输出

　　1）最短路线长度：从起点到终点经过的最少站数（站数计算不含起点，含终点）

　　2）最短路线：满足最短路线长度要求的所有路线（可能有多条路线，每条路线从起点到终点顺序输出途经的所有站点，包括起点和终点）

　　完成功能1和功能2满分100。

　　3）最优路线：换乘次数最少的最短路线（可能有多条路线）[本题20分，不计入总分，以附加分方式体现，比如“90+15”]

 

输入说明

　　地铁网络中的每一个站点用一个唯一的ID标识，ID是一个32位正整数；

　　一次输入一条线路，线路表示为一个站点ID数组；

　　例如{2, 3, 6, 9, 10}，表示这是一条I形线，2和10为两端，数组元素顺序和从一端到另一端途经站点的顺序一致；

　　例如{1, 3, 6, 7, 4, 1}，首尾站点一样，表示这是一条O形线，数组元素顺序和从站点1出发按某方向绕行一圈途经站点的顺序一致；

　　两条线路中出现了相同站点（如上面的3、6），表示两条线路在这些站点可相互换乘。

 

示例

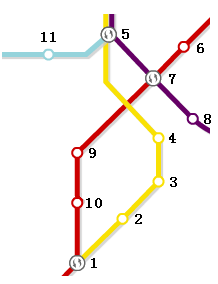
某城市的地铁信息，如图

Line1：{1,2,3,4,5};

Line2：{1,10,9,7,6};

Line3：{5,7,8};

Line4：{11,5};

从起点站1到终点站11

1）最短路线长度是5

2）最短路线有2条，分别是{1, 2, 3, 4,5,11}和{1,10,9,7,5,11}

3）最优路线有1条：{1, 2, 3, 4,5,11} （换乘一次）

 

 

　　

 

 

 

 

 

 

 

实现接口

　　说明：所有接口相互独立，没有调用顺序的要求（所谓“调用顺序”是例如：必须先调用2，再调用3，才能保证3的功能正确）

--------------------------------

(1) AddLine

Description　　

　　增加某条地铁线路

Prototype

　　void AddLine(unsigned int LineNo, unsigned int StationNum ,unsigned int *pStationArray)；

Input Param

　　LineNo 地铁线路号；

　　StationNum 该条地铁线中的站点数目，由调用者保证不小于2；

　　pStationArray 该条地铁线的所有站点信息，pStationArray指向的存储空间在函数外会被释 放，请自行申请存储空间；

Output Param

　　无

Return Value

　　无

--------------------------------

(2) CalcMinPathLen

Description

　　计算从起点站到终点站的最短路线长度

Prototype

　　int CalcMinPathLen(unsigned int SrcStation, unsigned int DesStation)；

Input Param

　　SrcStation 起点站；

　　DesStation 终点站；

Output Param

　　无

Return Value

　　起点站到终点站的最短路线长度

　　-1：任何出错情况（包括路线不存在、站点不存在、起点和终点重叠等等）

--------------------------------

(3) SearchMinPathes

Description

　　输出从起点站到终点站的最短路线

Prototype

　　int SearchMinPathes(unsigned int SrcStation, unsigned int DesStation, unsigned int* pPathNum, unsigned int* pPathLen,unsigned int **ppPathes);

Input Param

　　SrcStation 起点站；

　　DesStation 终点站；

Output Param

　　pPathNum 最短路线条数;

　　pPathLen 最短路线长度;

　　ppPathes 存储最短路线的内存地址，内存格式见下图,内存空间在本函数内申请，调用者释放；

Return Value

　　0：成功 -1：任何出错情况（包括路线不存在、站点不存在、起点和终点重叠等等）

--------------------------------

(4) SearchBestPathes（附加题）

Description

　　输出从起点站到终点站的最优路线

Prototype

int SearchBestPathes(unsigned int SrcStation,unsigned int DesStation,unsigned int *pPathNum, unsigned int* pPathLen,unsigned int** ppPathes);

Input Param

　　SrcStation 起点站；

　　DesStation 终点站；

Output Param

　　pPathNum 最优路线条数;

　　pPathLen 最短路线长度;

　　ppPathes 存储最短路线的内存地址，内存格式见下图,内存空间在本函数内申请，调用者释放；

Return Value

　　0：成功 -1：任何出错情况（包括路线不存在、站点不存在、起点和终点重叠等等）

--------------------------------

(5) Clear
Description 清空所有的线路信息

Prototype

　　 void Clear();

Input Param

　　 无

Output Param

　　无

Return Value

　　 无

 

 

算法提示

　　说明：提示的并不是本题的唯一算法，考生可根据情况自行选择是否采用。

1）最短路线长度算法提示

step1: 找到从起点出发，前进一站能到达的所有车站，记为SET1，若终点已包含在SET1中，则最短路线长度为1。

step2：对SET1中所有车站，找到前进一站能到达的所有车站，记为SET2，若终点已包含在SET2中，则最短路线长度为2。

...以此类推... stepn：

对SETn-1中所有车站，找到前进一站能到达的所有车站，记为SETn，若终点已包含在SETn中，则最短路线长度为n。

2）最短路线算法提示 最短路线长度算法在遍历过程中未记录路径信息，需要增加用作记录的数据结构设 计，该数据结构在最短路线长度的计算过程中生成。

3）最优路线算法提示 在求出最短路线的基础上，对每一条路线计算换乘最小次数，从所有路线方案中 选择最优解。

 

从此向下为后补内容，只提示算法的思想，不做算法：

以上图为例，假设我们要从 2 —> 8

 

 

序号 站号 父节点(序号) 0  2 (1) -1 1  1 (2)  0 2  3 (2)  0 3  10(3)  1 4  4(4)  2 5  9(5)  3 6  5(6)  4 7  7(7)  5 8  7(8)  6 9  11(8)  6 10  5(9)  7 11  6(9)  7 12  8(9)  7 13  6(10)  8 14  8(10)  8 15  9(10)  8      

（1）将起始站2加入表。

（2）找出序号0的站2可达相邻站1、3，此时1、3不在其父序｛2｝中，将1、3加入表，父节点设置为2的序号。

（3）找出序号1的站1可达相邻站10、2，此时10不在其父序｛2，1｝中，将10加入表，父节点设置为1(序号)；此时2在父序中，不做处理。

（4）找出序号2的站3可达相邻站2、4，此时4不在其父序｛2，3｝中，将4加入表，父节点设置为2(序号)；此时2在父序中，不做处理。

（5）找出序号3的站10可达相邻站1、9，此时9不在其父序｛2，1，10｝中，将9加入表，父节点设置为3(序号)；此时1在父序中，不做处理。

（6）找出序号4的站4可达相邻站3、5，此时5不在其父序｛2，3，4｝中，将5加入表，父节点设置为4(序号)；此时3在父序中，不做处理。 

（7）找出序号5的站9可达相邻站7、10，此时7不在其父序｛2，1，10，9｝中，将7加入表，父节点设置为5(序号)；此时10在父序中，不做处理。  

（8）找出序号6的站5可达相邻站7、11，此时7、11不在其父序｛2，3，4，5｝中，将11、7加入表，父节点设置为6(序号)。

此时可能看出，7被添加到表中两次，其实这两次是不一样的，仔细推敲吧。此表计算到最后是可以直接找出最优解和所有解，一种理想的数据结构和计算方法，直接拿满分不是更好吗？向下看。

（9）找出序号7的站7可达相邻站5、6、8、9，此时5、6、8不在其父序｛2，1，10，9，7｝中，将5、6、8加入表，父节点设置为7(序号)，此时9在父序中，不作处理。 

此时已经出现到达站8了，但是还不能结束计算，必须要将循环计算到父节点小于7的位置（站8父节点为7）才能结束，循环序号必须到达9(父节点为6，此上都小于7，此下都不小于7)，为什么？

（10）找出序号8的站7可达相邻站5、6、8、9，此时6、8、9不在其父序｛2，3，4，5，7｝中，将6、8、9加入表，父节点设置为8(序号)，此时5在父序中，不作处理。  

此时你应该看出来了，2-3-4-5-7-8 和 2-1-10-9-7-8 的间隔站是一样的，如果在第（9）步就停止计算，就遗漏了一个解，此时还没完，必须再走一次循环。

（11）找出序号9的站11可达相邻站5，此时5在其父序｛2，3，4，5，11｝中，不作处理。   

 

至此，循环已到达序号9，可以结束了。

 

现在要问：

　　最短线路有几条，请数一数8在表中出现的次数，2；

　　最短线路是多长，请随便找到一个8的位置，根据其父节点的值向上遍历，到达顶部（父节点为-1的位置）的遍历次数就是线路长度，比如我选序号14的8，根据其父节点向上遍历：8-7-9-10-1-2 ，长度为5

　　我们可以从所有的8开始反向遍历，看看谁的换线次数最少，（所有的线和站都有线性链表，计算遍历线性链表的中断次数），显然 8-7-5-4-3-2 在遍历时线性链表只中断一次，也就是只换乘了一次。也就是我们要找的最优解，将其输出即可2-3-4-5-7-8