 class="topic_img" alt=""/>
class="topic_img" alt=""/>
每次看电影预告片,我都会对新片激动不已。就像《星际穿越》的预告片,虽然我看了连剧情都不知道是什么,但我就是想看这部电影。而当我不得不等待什么东西时,唯一排解心焦的方法就是为这些东西写点什么。那,这就来吧,这次我想写的东西就是预告片里旋转的那个宇宙飞船(或者说太空站?我不清楚)。
为什么宇宙飞船要旋转?
这可不是一个简单的问题。让我先解释一下对于在太空飞行的宇航员来说何谓 “失重”,不过这里不会进行很详细的解释。下面是一些关键点:

《星际穿越》预告片截图。图片来源:视频截图
我想说的是,飞船当然受到引力,但引力都用来改变飞船的速度了。宇航员感到的“失重”,失去的其实是表观重量。而解决失重感的方法,就是对物体施加某种力,使之具有表观重量。
下面的图中有两个宇航员。左边那个站在地球上,右边那个站在宇宙飞船里。如果宇航员处于引力非常小的地方(如深空),唯一使他“感受到重量”的方法办法就是令地面对他施加支持力。这种情况下,右边的宇航员也能像左边的一样感受到重量。
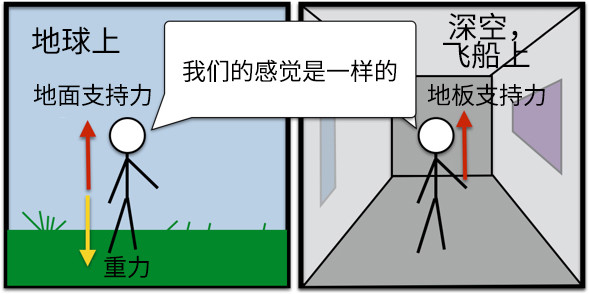
Rhett Allain 的灵魂画作。图片来源:Rhett Allain 编译:Calo
那么你要如何在太空里对宇航员施加这个力呢?这就要从力的性质入手了。或许你对下面这个公式并不陌生:

这个公式表明物体会在其受到的(净)合力下加速。记住,力和速度都是矢量——这点在下文挺重要的,不过现在我们只研究极短时间内物体的运动状况。在这个极端的时间段内,物体的平均加速度是:
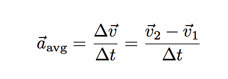
如果宇航员要获得表观重量,就需要受到地面施加的垂直向上的力,此时飞船的加速度方向同宇航员由脚部指向头部的方向一致。既然飞船有加速度,它的速度就会被改变。然而为了维持这个加速度,在一定时间内持续加速(增加速率)是件挺难的事(不过也不是不可能)。
不过,还有一个让宇航员获得加速度的方法,就是利用速度的矢量性质。既然速度是个矢量,改变速度的大小或方向都能需要加速度。哈!答案出来啦。如果你做匀速圆周运动,你就一直拥有加速度来改变速度方向。下面是一幅示意图:

以合适的速度做匀速圆周运动,飞船里的宇航员也可以获得表观重量。图片来源:Rhett Allain
做圆周运动需要加速度,这一点其实你早就知道了——每次开车转弯时,你都能感受到这股沿着角加速度方向的力。宇宙飞船在旋转时的原理亦是如此。宇航员(在旋转飞船里)受到的表观重量只取决于两点——圆周的半径和旋转的速度(通常用角速度ω表示)。下面是在旋转飞船里的表观重量的表达式(用重力加速度g来衡量):
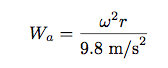
你会发现大的宇宙飞船(半径r比较大)不需要转得太快。如果你的飞船比较小,你就要转快点了。对了,这个表达式里的角速度的单位一定要是弧度每秒(rad/s)。
《星际穿越》里的宇宙飞船有多大呢?
现在我们有了表观重量的关系式,就可以用它来分析电影《星际穿越》里的旋转宇宙飞船了。记住,我将会用到许多假设,因为我没看过这电影。不过《娱乐周刊》说,旋转的飞船“能产生 1g 的重力” 。是的,这就是文章的原话,而且这句话当然是错的,因为事实上并没有“产生”重力,只是有表观重量产生而已。额,我是不是太挑剔了。
如果宇宙飞船提供 1g 的表观重量,我又知道它的旋转速度,我就可以计算它的半径了。很简单不是么。
《星际穿越》预告片中旋转的宇宙飞船。图片来源:视频截图
第一步是得到飞船的旋转速度。这不太难,因为几乎每个版本的预告片都展示了这艘飞船旋转的场景。现在我可以用视频分析软件(我喜欢用 Tracker Video Analysis)画飞船上某一点的运动图像。如果我定飞船的中心为原点,我就可以得到某一分离舱(或者其它什么东西)的角位移随时间变化的图像。

通过视频分析软件记录飞船的旋转过程。图片来源:Rhett Allain
将飞船上的位置标记出来挺难的,因为它在视频里太小了。然而你能从图上的趋势看出它是以一个不变的角速度旋转的。
从这条线的斜率,我可以得到角速度是 0.59 弧度每秒,加上“表观重量为 1g”的假设,可算出飞船的半径为 28.2 米或者直径为 56.4 米。我猜这不算太大,要知道国际空间站(带上太阳能电池板)有接近 100 米长呢。
文章题图:Youtube
编译来源 Wired, The Physics of a Spinning Spacecraft in Interstellar