斐波纳契数列(Fibonacci Sequence),又称黄金分割数列。
意大利的数学家列昂那多·斐波那契在1202年研究兔子产崽问题时发现了此数列,故又称为“兔子数列”.
设一对大兔子每月生一对小兔子,每对新生兔在出生一个月后又下崽(小兔子长到第三个月后每个月又生一对兔子),假若兔子都不死亡,问每个月的兔子总数为多少?
分析一下:
??? 第一个月小兔子没有繁殖能力,所以还是一对;
??? 两个月后,生下一对小兔对数共有两对;
??? 三个月以后,老兔子又生下一对,因为小兔子还没有繁殖能力,所以一共是三对;现在大兔子有三对,小兔子两对;
??? ------
依次类推可以列出下表: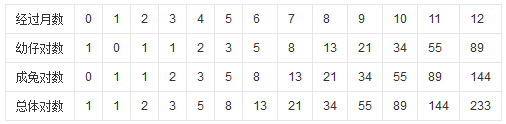
??? 幼仔对数=前月成兔对数
??? 成兔对数=前月成兔对数+前月幼仔对数
??? 总体对数=本月成兔对数+本月幼仔对数
??? 可以看出幼仔对数、成兔对数、总体对数都构成了一个数列。这个数列有关十分明显的特点,那是:前面相邻两项之和,构成了后一项。
用Java实现代码:
?
class="java" name="code">import java.util.Scanner; /** * Fibonacci * * @author weidong.feng */ public class Fibonacci { public static void main(String[] args){ Scanner scanner = new Scanner(System.in); System.out.print("please input this Fibonacci n:"); int n = scanner.nextInt(); // 假设输入为大于0的整数 // long startTime = System.nanoTime(); // 获取开始时间, 单位纳秒 long startTime = System.currentTimeMillis(); // 获取开始时间,单位毫秒 fib2(n); //for(int i=1; i<=n; i++){ // System.out.println("第 " + i + " 个月的兔子对数是: " + fibonacci2(i)); //} // long endTime = System.nanoTime(); // 获取结束时间, 单位纳秒 long endTime = System.currentTimeMillis(); // 获取结束时间,单位毫秒 System.out.println("程序运行时间: " + (endTime - startTime) + "ms"); } // 常规算法 private static void fib(int n){ double x = 1, y = 1; System.out.println("第 1 个 Fibonacci sequence data is: " + x); for (int i=1; i<n; i++){ System.out.println("第 " + (i + 1) + " 个 Fibonacci sequence data is: " + y); y = x + y; x = y - x; } } // 递归方式实现 /* * 时间复杂度为2的n次方 * 这种方式缺点: * 大量迭代不断消耗栈空间,效率低,甚至可能导致web服务器崩溃; * 函数自闭性比较弱(优秀的接口应该对输入输出可能出现的错误信息进行捕捉,并提供清楚明了的处理结果) * 很容易出现错误,调试困难。 * 实际应用中不建议使用这种方式 */ private static double fibonacci(int n){ if(n<=2) { return 1; }else { return fibonacci(n-1) + fibonacci(n-2); } } // 空间换时间,把计算过的所有数列用数组保存起来,需要用的时候直接查询即可 // 时间复杂度: ; 空间复杂度: ; private static void fib2(int n){ double arr[] = new double[n]; arr[0] = arr[1] = 1; for(int i=2; i<arr.length; i++){ arr[i] = arr[i-1] + arr[i-2]; } for(int i=0; i<arr.length; i++){ System.out.println("第 " + n + " 个Fibonacci数列值是: " + arr[i]); } } // 时间换空间(?还需斟酌优化?) private static double fibonacci2(int n){ double result = 0, temp1 = 0, temp2 = 1; for(int i=0; i<=n; i++){ if(i==0){ result = temp1; }else if(i==1){ result = temp2; }else{ result = temp1 + temp2; if(result < 0){ result = 0; break; } temp1 = temp2; temp2 = result; } } return result; } }
?
?
斐波那契数列还有两个有趣的性质: ⒈斐波那契数列中任一项的平方数都等于跟它相邻的前后两项的乘积加1或减1; ⒉任取相邻的四个斐波那契数,中间两数之积(内积)与两边两数之积(外积)相差1.在数学上,斐波纳契数列以如下被以递归的方法定义:F0=0,F1=1,Fn=F(n-1)+F(n-2)(n>=2,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用。
与黄金分割的关系
有趣的是:这样一个完全是自然数的数列,通项公式却是用无理数来表达的。而且当n趋向于无穷大时,后一项与前一项的比值的小数部分越来越逼近黄金分割0.618.
1÷1=1,2÷1=2,3÷2=1.5,5÷3=1.666...,8÷5=1.6,…………,89÷55=1.6181818…,…………233÷144=1.618055…75025÷46368=1.6180339889…...
越到后面,这些比值越接近黄金比.
? 证明:
??? a[n+2]=a[n+1]+a[n]
??? 两边同时除以a[n+1]得到:a[n+2]/a[n+1]=1+a[n]/a[n+1]
??? 若a[n+1]/a[n]的极限存在,设其极限为x
??? 则lim[n->∞](a[n+2]/a[n+1])=lim[n->∞](a[n+1]/a[n])=x
??? 所以x=1+1/x? 即x²=x+1
??? 所以极限是黄金分割比
?
如果你看到有这样一个题目:
??? 
某人把一个8*8的方格切成四块,拼成一个5*13的长方形,故作惊讶地问你:为什么64=65?
其实就是利用了斐波那契数列的这个性质【任取相邻的四个斐波那契数,中间两数之积(内积)与两边两数之积(外积)相差1.】:5、8、13正是数列中相邻的三项,事实上前后两块的面积确实差1,只不过后面那个图中有一条细长的狭缝,一般人不容易注意到。
?
在杨辉三角中隐藏着斐波那契数列
将杨辉三角左对齐,成如图所示排列,将同一斜行的数加起来,即得一数列1、1、2、3、5、8、…

?
相关数学问题
1. 排列组合
??? 有一段楼梯有10级台阶,规定每一步只能跨一级或两级,要登上第10级台阶有几种不同的走法?
??? 这就是一个斐波那契数列:
???? 登上第一级台阶有一种登法;登上两级台阶,有两种登法;登上三级台阶,有三种登法;登上四级台阶,有五种登法……
??? 1,2,3,5,8,13……所以,登上十级,有89种走法。
?
??? 类似的,一枚均匀的硬币掷10次,问不连续出现正面的可能情形有多少种?
??? 答案是(1/√5)*{[(1+√5)/2]^(10+2) - [(1-√5)/2]^(10+2)}=144种
?
2. 数字谜题
三角形的三边关系定理和斐波那契数列的一个联系:
??? 现有长为144cm的铁丝,要截成n小段(n>2),每段的长度不小于1cm,如果其中任意三小段都不能拼成三角形,则n的最大值为多少?
??? 分析:由于形成三角形的充要条件是任何两边之和大于第三边,因此不构成三角形的条件就是任意两边之和不超过最大边。截成的铁丝最小为1,因此可以放2个1,第三条线段就是2(为了使得n最大,因此要使剩下来的铁丝尽可能长,因此每一条线段总是前面的相邻2段之和),依次为:1、1、2、3、5、8、13、21、34、55,以上各数之和为143,与144相差1,因此可以取最后一段为56,这时n达到最大为10。
??? 我们看到,“每段的长度不小于1”这个条件起了控制全局的作用,正是这个最小数1产生了斐波那契数列,如果把1换成其他数,递推关系保留了,但这个数列消失了。这里,三角形的三边关系定理和斐波那契数列发生了一个联系。
?
?