线性表
定义:是最常用的,也是最简单的数据结构,是长度为n个数据元素的有序的序列。
含有大量记录的线性表叫文件
记录:稍微复杂的线性表里,数据元素为若干个数据项组成,这时把一个数据元素叫记录
结构特点:在非空有限的条件下,存在唯一的一个表头结点,唯一的一个表尾结点,除去第一个元素之外,每个数据元素都只有一个前驱,除去最后一个元素之外,每一个数据元素都只有一个后继。
注意:线性表中的数据元素可以是各种各样的,但同一线性表中的元素必定具有相同特性(属于同一数据对象,类似数组)。线性表的数据元素间有序偶关系。
线性表的顺序表示和实现
有一组地址连续的内存单元,在这些连续的内存单元里,顺次地存储线性表里的数据元素
特点:逻辑地址和物理地址都是连续的,适合随机存取。假设&a1为线性表的基址,每个数据元素占据L个存储单位。那么表里第i个元素的存储地址:
&a(i) = &a(1) + (i - 1)x L
线性表的顺序表示结构(顺序映象)也叫顺序表,顺序表中元素的逻辑关系和物理位置一致,是一种随机存取的存储结构。
(类似高级语言里的数组,通常用数组描述数据结构的顺序存储结构)。
如果用数组表示顺序表,那很简单,也不实用,不能改变存储容量,下面是动态分配的顺序表的表示和操作
ADT.h头文件
1 /************************************************************************/ 2 /* 功 能:声明常量和函数原型的头文件,线性表的动态分配顺序存储结构 3 /* 作 者:dashuai 4 /************************************************************************/ 5 #include <stdio.h> 6 #include <stdlib.h> 7 #define LIST_INIT_SIZE 100//线性表初始化存储空间分配 8 #define LISTINCREMENT 10//线性表存储空间的分配增量 9 10 typedef struct{//此时可以省去结构标记 11 int *elem;//线性表基址 12 int length;//当前表长 13 int listsize;//当前为线性表分配的存储容量 14 } SqList;//为结构起的别名SqList 15 16 //线性表常用的有13个操作,归为4类 17 18 /************************************************************************/ 19 /*第一类:初始化操作,记住各种数据结构开始使用都要初始化 */ 20 /************************************************************************/ 21 22 //1、线性表的初始化,构造一个空的线性表 23 int InitList(SqList *L);//因为要改变线性表,必须用指针做参数 24 25 /************************************************************************/ 26 /*第二类:销毁操作,记住各种数据结构使用了都要有销毁的步骤 */ 27 /************************************************************************/ 28 29 //2、销毁,释放内存操作 30 void Destory(SqList *L);//直接把内存释放的操作!类似与free() 31 32 /************************************************************************/ 33 /* 第三类:引用型操作,操作不改变线性表里的数据元素,也不改变他们之间的关系*/ 34 /************************************************************************/ 35 36 //3、判空操作,若线性表已经存在,为空白则返回true,否则返回false 37 void ListEmpty(SqList L); 38 39 //4、求长度操作,若线性表已经存在,则返回表L中元素个数 40 int ListLength(SqList L); 41 42 //5、定位操作:线性表 L 已存在,返回 L 中第 1 个与 e 满足相等关系的元素的位序。 43 //若这种元素不存在,则返回 0。 44 int LocateElem(SqList L, int e); 45 46 //6、求元素后继,初始条件:线性表 L 已存在。若 cur_e是 L 中的元素,则打印它的后继 47 //否则操作失败 48 void NextElem(SqList L, int cur_e); 49 50 //7、得到指定的元素值,线性表 L 已存在 51 //1≤i≤表长。用 e 返回 L 中第 i 个元素的值。 52 int GetElem(SqList L, int i, int e); 53 54 //8、求元素前驱,线性表L已经存在,若cur_e是L的数据元素,则返回前驱 55 //否则操作失败 56 void PriorElem(SqList L, int cur_e); 57 58 //9、遍历表中元素,线性表 L 已存在,打印出表中每个元素 59 //无法遍历,则操作失败。 60 void ListTraverse(SqList L); 61 62 /************************************************************************/ 63 /* 第四类:加工型操作 */ 64 /************************************************************************/ 65 66 //10、把表清空(不释放内存):线性表 L 已存在,将 L 重置为空表。 67 void ClearList(SqList *L); 68 69 //11、给表某元素赋值,线性表 L 已存在 70 //L 中第 i 个元素赋值为 e 的值。 71 void PutElem(SqList *L, int i, int e ); 72 73 //12、插入操作,线性表 L 已存在,在 L 的第 i 个元素之前插入新的元素 e,L 的长度增 1。 74 void ListInsert(SqList *L, int i, int e ); 75 76 //13、caozuo.html" target="_blank">删除操作,表 L 已存在且非空,。删除 L 的第 i 个元素,并用 e 返回其值,长度减 1。 77 void ListDelete(SqList *L, int i, int *e ); 78 79 /************************************************************************/ 80 /* 额外的几个复杂操作 */ 81 /************************************************************************/ 82 83 //1、合并线性表AB,把在线性表B里,但不存在于线性表A的元素插入到A中 84 //只改变A,不修改B 85 void Union(SqList *LA, SqList LB); 86 87 //2、合并线性表AB,AB的元素按值非递减有序的排列,要把A和B归并为一个新表C,且C的元素依然是按照值非递减的有序排列 88 void MergeList(SqList LA, SqList LB, SqList *LC); 89 90 //头文件
ADTList.c文件
1 /************************************************************************/ 2 /*函数定义在此文件 */ 3 /************************************************************************/ 4 #include "ADT.h" 5 /************************************************************************/ 6 /*第一类:初始化操作,记住各种数据结构开始使用都要初始化 */ 7 /************************************************************************/ 8 9 //注意c数组下标从0开始,但是用户并不知道,一般都是选择从1到length的位置,以用户的角度看问题 10 11 //1、线性表的初始化,构造一个空的线性表,因为要改变线性表,必须用指针做参数 12 int InitList(SqList *L) 13 { 14 //在堆中为线性表分配内存,初始化elem为该内存空间的首地址(基址) 15 L->elem = (int *)malloc(LIST_INIT_SIZE * sizeof(int));//结构里只是存储了表的地址值,而表本身存储在其他地方 16 //判断是否分配成功 17 if (!L->elem)//如果 !L->elem 为真(为空),执行下面代码 18 { 19 printf("线性表内存分配失败!退出程序。\n"); 20 exit(1);//函数异常退出,返回给操作系统1 21 } 22 //表内存空间分配成功 23 L->length = 0;//开始是空表,没有存储任何元素,故表长置为0 24 //当前为线性表分配的存储容量 25 L->listsize = LIST_INIT_SIZE;//初始化表的存储容量,这是当前表最大的存储量 26 return 0;//分配成功返回0 27 }
虽然在堆开辟了一块内存空间给线性表,但是需要设置一个变量listsize,来显式的表明表的最大存储容量的数值,方便程序使用(分配的空间内存大小和表长是两回事,表长是表内当前的元素个数,也就是此时线性表当前的存储容量)
1 /************************************************************************/ 2 /*第二类:销毁操作,记住各种数据结构使用了都要有销毁的步骤 */ 3 /************************************************************************/ 4 5 //2、释放内存,销毁表操作,直接把内存释放的操作!类似free()和c++的delete操作符 6 //注意:用malloc函数分配的空间在释放时是连续释放的,即将物理地址相邻的若干空间全部释放 7 //所以顺序表销毁可以只释放基址,就自动释放所有空间,而链表要一个一个的把节点删除 8 void Destory(SqList *L) 9 { 10 if (L->elem)//如果当前表还存在 11 { 12 free(L->elem);//销毁之 13 //内存都没了,整个表也就不存在了,别的不用管。 14 printf("本线性表已销毁!\n"); 15 } 16 }
注意:用malloc函数分配的空间在释放时是连续释放的,即将物理地址相邻的若干空间全部释放,所以顺序表销毁可以只释放基址自动释放所有空间,而链表要一个一个的把节点删除
1 /************************************************************************/ 2 /* 第三类:引用型操作,操作不改变线性表里的数据元素,也不改变他们之间的关系 3 /************************************************************************/ 4 5 //3、判空操作 6 void ListEmpty(SqList L) 7 { 8 //判断表是否存在 9 if (L.elem) 10 { 11 //判断是否存储了内容 12 if (0 == L.length) 13 { 14 puts("本表为空!");//自动换行 15 } 16 else 17 { 18 puts("表不为空!"); 19 } 20 } 21 else 22 { 23 puts("表不存在!"); 24 } 25 }
0 == L.length,个人喜欢这种写法,避免出错,如果一时疏忽,写=,则编译报错!常量不能作为左值出现,来提醒自己
1 //4、求长度操作,若线性表已经存在,则返回表L中元素个数 2 int ListLength(SqList L) 3 { 4 if (L.elem) 5 { 6 return L.length; 7 } 8 puts("表不存在,无法求长度!"); 9 return 0; 10 }
1 //5、定位操作:线性表 L 已存在,返回 L 中第 1 个与 e 满足相等关系的元素位置。 2 int LocateElem(SqList L, int e) 3 { 4 int i;//定位 5 for (i = 0; i < L.length; i++) 6 { 7 //数组名本身就是数组的首地址 8 if (e == L.elem[i] && i < L.length) 9 { 10 printf("定位成功,该元素的位置 = %d\n", i + 1); 11 return i + 1; 12 } 13 } 14 puts("定位失败!没有找到该元素"); 15 return 0; 16 }
个人觉得因为已经有初始化操作和判空操作,则其余函数不用再写判断表存在否的语句
c的数组下标从0开始,但是还是习惯1对应第一个数据元素,以此类推……
1、定位算法的时间复杂度分析
假设表长为n
最好的情况,如果第一个元素就满足关系,那么时间复杂度为0(1)
最坏的情况,如果最后一个元素满足关系或者没有满足关系的(依然还是比较了),时间复杂度为0(n)
2、算法平均时间复杂度:
显然是和表长成正比的,为0(n)
1 //6、求元素后继,线性表 L 已存在。若 cur_e是 L 中的元素,返回后继 2 void NextElem(SqList L, int cur_e) 3 { 4 int i = LocateElem(L, cur_e);//先定位参照元素的位置 5 6 if (0 != i) 7 { 8 if (i == L.length) 9 { 10 puts("这是最后一个元素,没有后继!"); 11 } 12 else 13 { 14 printf("%d的后继是%d\n", L.elem[i - 1], L.elem[i]); 15 } 16 } 17 else 18 { 19 puts("表中没有这个元素!"); 20 } 21 }
注意:区分数组角度看问题和用户角度看问题,表长范围等不要混淆。
1 //7、得到指定的元素值,线性表 L 已存在, e 返回 L 中第 i 个元素的值。 2 int GetElem(SqList L, int i, int e) 3 { 4 if (i < 1 || i > L.length) 5 { 6 puts("超出了查找范围,重新输入!"); 7 return 0; 8 } 9 e = L.elem[i - 1]; 10 return e; 11 }
这里没有打印,只是返回了值,不太好,因为出现了一个问题,函数内部的e是局部变量,且是值传递参数类型,函数执行完毕,e的内存消失,不再起作用,对实参没有影响。在函数外打印e的值得不到正确值
1 int GetElem(SqList L, int i, int *e) 2 { 3 if (i < 1 || i > L.length) 4 { 5 puts("超出了查找范围,重新输入!"); 6 return 0; 7 } 8 *e = L.elem[i - 1]; 9 printf("%d\n", *e); 10 return *e; 11 }
改进:或者增加函数内的打印语句,或者把e变为指针类型的变量,可以修改实参,相应的声明里也要修改!
1 /8、求元素前驱,线性表L已经存在,若cur_e是L的数据,则返回前驱 2 void PriorElem(SqList L, int cur_e) 3 { 4 int i = LocateElem(L, cur_e);//如果定位失败返回0 5 6 if (0 != i) 7 { 8 if (1 == i) 9 { 10 puts("这是第一个元素,没有前驱!"); 11 } 12 else 13 { 14 printf("找到了%d的前驱%d \n", L.elem[i - 1], L.elem[i - 2]); 15 } 16 } 17 else 18 { 19 puts("找不到这个元素!"); 20 } 21 }
注意一下: L.elem[i - 1]和 L.elem[i - 2]与i的关系
1 //9、遍历表中元素,线性表 L 已存在,打印出表中每个元素 2 void ListTraverse(SqList L) 3 { 4 int i; 5 6 for (i = 0; i < L.length; i++) 7 { 8 printf("%5d", L.elem[i]); 9 } 10 11 }
%5d,宽度为5打印输出
1 /************************************************************************/ 2 /* 第四类:加工型操作 */ 3 /************************************************************************/ 4 5 //10、把表清空(不释放内存),线性表 L 已存在,将 L 重置为空表。 6 void ClearList(SqList *L) 7 { 8 if (L->elem) 9 { 10 L->length = 0;//顺序表置空,表长为0即可 11 } 12 }
和销毁内存区分
1 //11、给表元素赋值,线性表 L 已存在,1≤i≤LengthList(L) 2 //L 中第 i 个元素赋值为 e 3 void PutElem(SqList *L, int i, int e ) 4 { 5 if (i < 1 || i > L->length) 6 { 7 puts("超出表范围!"); 8 } 9 L->elem[i - 1] = e; 10 }
常用的,也是比较重要的插入和删除算法
1 //12、插入操作,线性表 L 已存在,1≤i≤LengthList(L)+1。在 L 的第 i 个元素之前插入新的元素 e,L 的长度增 1。 2 void ListInsert(SqList *L, int i, int e ) 3 { 4 SqList *NL;//声明一个额外的结构指针指向重新分配的表内存空间 5 int *j; 6 int *k; 7 //注意c数组下标从0开始,但是用户并不知道,一般都是选择从1到length的位置,以用户的角度看问题 8 //在元素i之前插入,则把i和i后面的全部元素顺次后移一位 9 if (i < 1 || i > L->length + 1)//最后一个元素后一位插入合法,不用移动直接插即可 10 { 11 puts("超出表范围!"); 12 } 13 //考虑问题要全,因为可能会不止一次插入操作,早晚会超出表的存储容量 14 else if (L->length >= L->listsize) 15 { 16 //重新分配内存,增加存储空间 17 NL->elem = (int *)realloc(L->elem, (L->listsize + LISTINCREMENT) * sizeof(int)); 18 if (!NL->elem)//分配失败,返回NULL 19 { 20 exit(0);//退出 21 } 22 //分配成功 23 L->elem = NL->elem;//得到扩大之后的新基址 24 } 25 //指示用户的实际插入位置 26 j = &(L->elem[i - 1]);//数组下标从0开始 27 //最后一个数据元素的实际位置是length-1 28 for (k = &(L->elem[L->length - 1]); k >= j; k--)//这里k--不是1的减量!而是指针的减量操作,每次是int类型字节大小变化 29 { 30 *(k + 1) = *k;//从j到k的元素顺次后移一位 31 } 32 *j = e;//完成插入 33 L->length++;//别忘表长加1 34 }
1、需要注意一下运算符优先级,箭头(间接运算符)的优先级很高,高于取地址&
2、解析realloc函数
它可以对给定的指针所指的空间进行扩大或者缩小,原有内存的中内容将保持不变。对于缩小,则被缩小的那一部分的内容会丢失 ,realloc 并不保证调整后的内存空间和原来的内存空间保持同一内存地址。realloc 返回的指针很可能指向一个新的地址。因为realloc是从堆上分配内存,当扩大内存空间,realloc直接从堆上现存的数据后面的那些字节中获得附加的字节,但如果数据后字节不够,就用堆上第一个有足够大小的自由块,现存的数据被拷贝至新的位置,而老块则放回到堆上。
在代码中,如果我们采用i = (int*)realloc(i, 2*sizeof(int))的重新分配内存方式,有以下两种情况:
分配成功:
realloc函数完成后,i 曾经指向的旧内存自动free掉。
分配失败,返回NULL值:
此时,i 原来指向的内存还没有被free掉,而现在又找不到地址,这样就出现memory leak!
解决办法:定义另一个指针j用于接收realloc返回值,判断是否成功,成功则将 j 赋给 i
3、插入算法的时间复杂度分析:
问题规模是表的长度,值为 n。 算法的时间主要花费,在向后移动元素的 for 循环语句上。该语句的循环次数为 (n– i +1),所需移动结点的次数不仅依赖于表的长度 n,而且还与插入位置 i 有关。
当插入位置在表尾 (i=n +1) 时,不需要移动任何元素;这是最好情况,其时间复杂度 O(1)。 当插入位置在表头 (i = 1) 时,所有元素都要向后移动,循环语句执行 n 次,这是最坏情况,其时间复杂度 O(n)。 4、插入算法的平均时间复杂度: 设 pi 为第 i 个元素之前插入一个元素的概率,则在长度为 n 的线性表中插入一个元素时所需移动元素次数的期望值为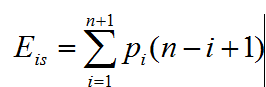 假设在n+1个位置上,插入的概率一样,那么pi = 1/(n+1);
E = pi【(n)+(n-1)+ ……+ 3 + 2 + 1】 =pi x( n(n+1)/ 2) = n / 2
由此可见,在顺序表上做插入运算,平均要移动
假设在n+1个位置上,插入的概率一样,那么pi = 1/(n+1);
E = pi【(n)+(n-1)+ ……+ 3 + 2 + 1】 =pi x( n(n+1)/ 2) = n / 2
由此可见,在顺序表上做插入运算,平均要移动
一半元素。当表长 n 较大时,算法的效率相当低。
插入
算法的
平均时间复杂度为 O(n)。
1 //13、删除操作,表 L 已存在且非空,1≤i≤LengthList(L)。删除 L 的第 i 个元素,并用 e 返回其值,长度减 1。 2 void ListDelete(SqList *L, int i, int *e ) 3 { 4 int *p; 5 6 if (i < 1 || i > L->length) 7 { 8 puts("i的值不合法!重新输入!"); 9 } 10 else 11 { 12 //找到被删除元素的实际位置 13 p = &(L->elem[i - 1]); 14 *e = L->elem[i - 1]; 15 //p(不包含p)后面的元素依次前移一位 16 for (; p < &(L->elem[L->length - 1]); p++) 17 { 18 *p = *(p + 1); 19 } 20 L->length--; 21 } 22 }
1、这里e使用指针变量,这样形参就可以修改实参!
2、删除算法的时间复杂度分析
算法的时间主要花费在向前移动元素的 for 循环语句上。该语句的循环次数为 (n – i)。由此可看出,所需移动结点的次数不仅依赖于表的长度 n,而且还与删除位置 i 有关。
当删除位置在表尾 (i = n) 时,不需要移动任何元素;这是最好情况,其时间复杂度 O(1)。 当删除位置在表头 (i = 1) 时,有 n -1 个元素要向前移动,循环语句执行 n -1 次,这是最坏情况其时间复杂度 O(n)。 3、算法的平均时间复杂度: 设 qi 为删除第 i 个元素的概率,则在长度为 n 的线性表中删除一个元素时所需移动元素次数的期望值为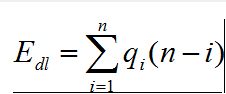 假设,每一个位置的元素被删除的概率都一样,那么qi = 1 / n
E = qi【(n-1)+(n-2)+……+3+2+1】=1/n x ((n-1)n / 2)=(n - 1)/ 2
可见,在顺序表上做删除运算,平均也要移动表上
假设,每一个位置的元素被删除的概率都一样,那么qi = 1 / n
E = qi【(n-1)+(n-2)+……+3+2+1】=1/n x ((n-1)n / 2)=(n - 1)/ 2
可见,在顺序表上做删除运算,平均也要移动表上
一半元素。当表长 n 较大时,算法的效率相当低。算法的平
均时间复杂度为 O(n)。
1 /************************************************************************/ 2 /* 额外的几个复杂操作 */ 3 /************************************************************************/ 4 5 //1、合并线性表AB,把在线性表B里,但不存在于线性表A的元素插入到A中 6 //只改变A,不修改B 7 void Union(SqList *LA, SqList LB) 8 { 9 int i; 10 int e; 11 int lengthA = LA->length; 12 int lengthB = LB.length; 13 14 //在B里依次取得每个数据元素,顺序在A里比较,若不存在则插入 15 for (i = 1; i <= lengthB; i++) 16 { 17 GetElem(LB, i, &e); 18 if (!LocateElem(*LA, e))//A里没有这个元素 19 { 20 //插入到A尾部 21 /*lengthA++; 22 ListInsert(LA, lengthA, e);*/ 23 ListInsert(LA, ++lengthA, e); 24 } 25 } 26 Destory(&LB); 27 }
算法复杂度分析:
GetElem函数执行和表长没有关系,插入函数每次都在最后一位插入,执行时间和表长也没有关系,而LocateElem函数执行时间和表长有关系,无序合并算法的时间复杂度主要取决于LocateElem的执行时间,前面分析过,LocateElem时间复杂度:0(lengthA),那么本算法的时间复杂度为:O(lengthA x lengthB)
1 //2、合并线性表AB,AB的元素按值非递减有序的排列,要把A和B归并为一个新表C,且C的元素依然是按照值非递减的有序排列 2 void MergeList(SqList LA, SqList LB, SqList *LC) 3 { 4 InitList(LC);//构造新表c 5 int lengthA = LA.length; 6 int lengthB = LB.length; 7 int lengthC = LC->length;//C表初始化为空表,0 8 int i = 1;//i标记LA 9 int j = 1;//j标记LB 10 int iLA; 11 int jLB; 12 13 while ((i <= lengthA) && (j <= lengthB)) 14 { 15 //分别取得元素值,比较 16 GetElem(LA, i, &iLA); 17 GetElem(LB, j, &jLB); 18 if (iLA <= jLB)//LA,LB都是非递减排列 19 { 20 lengthC++;//总在末尾插入 21 ListInsert(LC, lengthC, iLA); 22 i++; 23 } 24 else 25 { 26 ListInsert(LC, ++lengthC, jLB); 27 j++; 28 } 29 } 30 //AB不会同时比完,一定会有一个表完全插入到c之后,另一表剩余 31 while (i <= lengthA) 32 { 33 GetElem(LA, i++, &iLA); 34 ListInsert(LC, ++lengthC, iLA);//本来AB就有序,直接全部插入到C末尾即可 35 } 36 //or 37 while (j <= lengthB) 38 { 39 GetElem(LB, j++, &jLB); 40 ListInsert(LC, ++lengthB, jLB); 41 } 42 }
算法时间复杂度分析:
不论表AB,哪个表,肯定有一个表先完全比完,比如是LA,比较了lengthA次。之后,两个while语句,就执行一个,就是LB剩余的元素顺次插入C表剩余次数的过程,加上之前LB和LA的比较次数,那么综合得其时间复杂度为0(lengthA + lengthB)
本算法的另一种思路,不依靠前面已经定义好,能拿来就用的函数,使用指针进行比较,赋值
1 //2、合并线性表AB,AB的元素按值非递减有序的排列,要把A和B归并为一个新表C,且C的元素依然是按照值非递减的有序排列 2 void MergeList(SqList LA, SqList LB, SqList *LC) 3 { 4 //还是先构造表C,不用下标,只能使用指针来操作 5 LC->listsize = LA.length + LB.length; 6 LC->length = LA.length + LB.length; 7 int *c = (int *)malloc((LC->listsize) * sizeof(int)); 8 int *a = LA.elem; 9 int *b = LB.elem; 10 int *lastA = LA.elem + (LA.length - 1) * sizeof(int); 11 int *lastB = LB.elem + (LB.length - 1) * sizeof(int); 12 LC->elem = c; 13 if (!LC->elem) 14 { 15 puts("c表构建失败!"); 16 exit(-1); 17 } 18 while (a <= lastA && b <= lastB) 19 { 20 if (*a <= *b) 21 { 22 *c++ = *a++;//从右到左运算,先计算*c = *a,后a++,c++ 23 } 24 else 25 { 26 *c++ = *b++; 27 } 28 } 29 while (a <= lastA) 30 { 31 *c++ = *a++; 32 } 33 while (b <= lastB) 34 { 35 *c++ = *b++; 36 } 37 }
1、时间复杂度还是0(lengthA + lengthB)
2、这里发现,当线性表的元素无序的时候,进行插入操作的时间复杂度比有序的时候的时间复杂度要大的多。
因为,有序的线性表AB,比如依次递增(都不相等),则比较AB元素大小时,不用把B的每一个元素都和A比较!因为可以保证前面的元素肯定是小于后面的。这样大大节省了运行时间!
3、还有发现如果是两表归并到新表里,那么新表开始就是空的,只需要依次插入即可(换句话说就是依次赋值即可),不用移动元素,而如果是A归并到B里(反之亦然),那么保持有序的话,就需要B的元素时不时的移动,耽误时间。
故,当使用线性表表示数组或者集合等等吧,进行操作的时候,最好是先给表排序,或者有归并,则归并到新的空表。
到此,关于线性表里的顺序表的概念和常用算法就算分析完毕,经常用的操作的是初始化,销毁,清空,判空,定位,插入,删除,遍历,前驱,后继,赋值,得到元素,求长度,接下来分析的是经常用到的链表。