前几天看科幻小说<三体>,讲到有种武器叫水滴,是三体人用于对付地球人的.这一节将介绍几种水滴形的数学公式.
<三体>书中对水滴的描述如下:
当全世界第一次看到探测器的影像时,所有人都陶醉于它那绝美的外形。这东西真的是太美了,它的形状虽然简洁,但造型精妙绝伦,曲面上的每一个点都恰到好处,使这滴水银充满着飘逸的动感,仿佛每时每刻都在宇宙之夜中没有尽头地滴落着。它给人一种感觉:即使人类艺术家把一个封闭曲面的所有可能形态平滑地全部试完,也找不出这样一个造型。它在所有的可能之外,即使柏拉图的理想国中也没有这样完美的形状,它是比直线更直的线,是比正圆更圆的圆,是梦之海中跃出的一只镜面海豚,是宇宙间所有爱的结晶...美总是和善联在一起的,所以,如果宇宙中真有一条善恶分界线的话,它一定在善这一面。
使用自己定义语法的脚本代码生成数学图形.相关软件参见:数学图形可视化工具,该软件免费开源.QQ交流群: 367752815
我之前写过有关水滴线的文章,数学图形(1.15) 水滴线,那是讲的二维曲线,而这一节给大家带来的是三维水滴形.当然水滴形就是由一个水滴线旋转180度,或半个水滴线旋转360度而生成的.
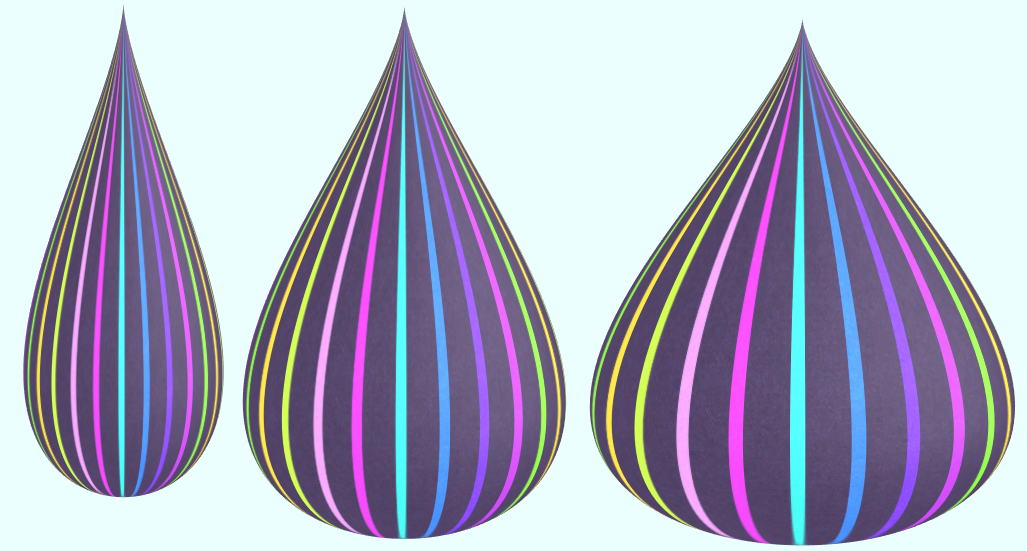
(1)水滴
vertices = D1:100 D2:100 u = from 0 to (PI) D1 v = from 0 to (2*PI) D2 a = 10 b = rand2(0.25, 1) m = a/2*(1 + cos(u)) n = a*a/64*(sin(2*u) + 2*sin(u))*b x = n*cos(v) z = n*sin(v) y = array_max(m)-m
(2)Ding-Dong
#http://mathworld.wolfram.com/Ding-DongSurface.html # x^2+y^2=(1-z)z^2 vertices = 360 v = from -1 to 1 D2 x = v*sqrt(0.5 - v/2) y = v a = 10 x = x*a y = y*a
#http://mathworld.wolfram.com/Ding-DongSurface.html # x^2+y^2=(1-z)z^2 vertices = D1:100 D2:100 u = from 0 to (PI*2) D1 v = from -1 to 1 D2 x = v*sqrt(0.5 - v/2)*cos(u) y = v z = v*sqrt(0.5 - v/2)*sin(u) a = 10 x = x*a y = y*a z = z*a

(3)kiss
#http://mathworld.wolfram.com/KissSurface.html # x^2+y^2=(1-z)z^4 vertices = 360 v = from -1 to 1 x = v*v*sqrt(0.5 - v/2) y = v a = 10 x = x*a y = y*a
#http://mathworld.wolfram.com/KissSurface.html # x^2+y^2=(1-z)z^4 vertices = D1:100 D2:100 u = from 0 to (PI*2) D1 v = from -1 to 1 D2 x = v*v*sqrt(0.5 - v/2)*cos(u) y = v z = v*v*sqrt(0.5 - v/2)*sin(u) a = 10 x = x*a y = y*a z = z*a

(4)Larme
#http://www.mathcurve.com/courbes2d/larme/larme.shtml vertices = D1:100 D2:100 u = from 0 to (PI) D1 v = from 0 to (2*PI) D2 n = rand2(1, 10) m = 10*cos(u) n = 10*sin(u)*pow(sin(u/2), n) x = n*cos(v) z = n*sin(v) y = m

(5)Pear
#http://www.2dcurves.com/quartic/quarticp.html#pearshapedcurve vertices = D1:100 D2:100 u = from 0 to (2*PI) D1 v = from 0 to (PI) D2 m = -1 - sin(u) n = 0.5*(1 + sin(u))*cos(u) x = n*cos(v) z = n*sin(v) y = array_max(m)-m

(6)Teardrop
#http://mathworld.wolfram.com/TeardropCurve.html vertices = D1:100 D2:100 u = from 0 to (PI) D1 v = from 0 to (2*PI) D2 m = rand2(0, 10) n = 10*sin(u)*pow(sin(u/2), m) y = 10*cos(u) x = n*cos(v) z = n*sin(v)
