第一题:

答案:
第二题:
烧一根不均匀的绳,从头烧到尾总共需要1个小时。现在有若干条材质相同的绳子,问如何用烧绳的方法来计时一个小时十五分钟呢?
解题思路:
烧一根这样的绳,从头烧到尾1个小时。由此可知,头尾同时烧共需半小时。同时烧两根这样的绳,一个烧一头,一个烧两头;当烧两头的绳燃尽时,共要半小时,烧一头的绳继续烧还需半小时;如果此时将烧一头的绳的另一头也点燃,那么只需十五分钟。
参考答案:
a绳从两头烧,同时b绳从一头烧,当a绳烧尽时,灭掉b绳,同时c绳从两头烧,在c绳烧尽时,b绳从两头烧,结束时即为1小时15分钟。
--------------------------------------------------------------------------------
第三题:
12个球一个天平,现知道只有一个和其它的重量不同,问怎样称才能用三次就找到那个球。13个呢?(注意此题并未说明那个球的重量是轻是重,所以需要仔细考虑)
答案:
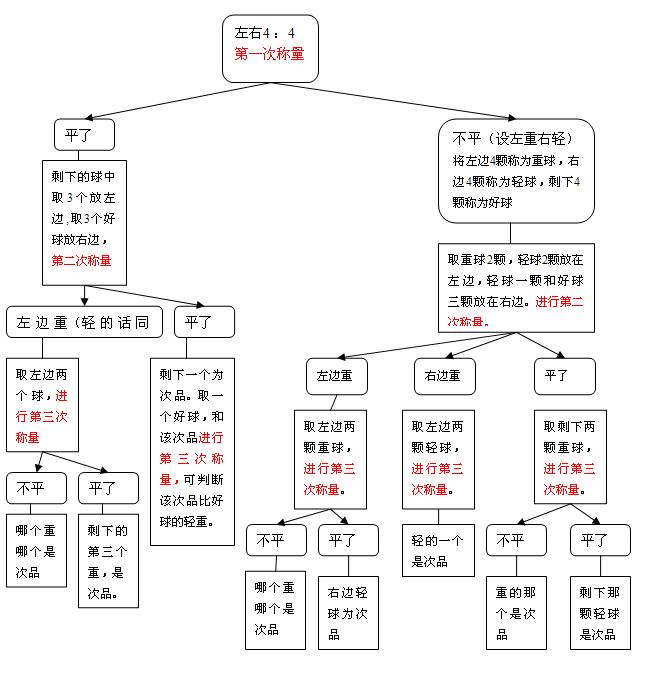
文字描述:
第一次:4,4 如果平了:
那么剩下的球中取3放左边,取3个好球放右边,称:
如果左边重,那么取两个球称一下,哪个重哪个是次品,平的话第三个重,是次品,轻的话同理
如果平了,那么剩下一个次品,还可根据需要称出次品比正品轻或者重
如果不平:
那么不妨设左边重右边轻,为了便于说明,将左边4颗称为重球,右边4颗称为轻球,剩下4颗称为好球
取重球2颗,轻球2颗放在左侧,右侧放3颗好球和一颗轻球
如果左边重
称那两颗重球,重的一个次品,平的话右边轻球次品
如果右边重
称左边两颗轻球,轻的一个次品
如果平
称剩下两颗重球,重的一个次品,平的话剩下那颗轻球次品
13个球:
第一次:4,4,如果平了
剩5颗球用上面的方法仍旧能找出次品,只是不能知道次品是重是轻
如果不平,同上
--------------------------------------------------------------------------------
第四题:
你让工人为你工作7天,回报是一根金条,这个金条平分成相连的7段,你必须在每天结束的时候给
他们一段金条。如果只允许你两次把金条弄断,你如何给你的工人付费?
答案:分成1,2,4三段,
第一天给1,第二天给2取回1,第3天给1,第4天给4取回1、2,第5天给1,第6天给2取回1,第七天给1。
--------------------------------------------------------------------------------
第五题:
你有四个装药丸的罐子,每个药丸都有一定的重量,被污染的药丸是没被污染的药丸的重量+1。只称量一次,如何判断哪个罐子的药被污染了?
答案:四个罐子中分别取1,2,3,4颗药丸,称出比正常重多少,即可判断出那个罐子的药被污染。
--------------------------------------------------------------------------------
第六题:
第一题 . 五个海盗抢到了100颗宝石,每一颗都一样大小和价值连城。他们决定这么分:
抽签决定自己的号码(1、2、3、4、5)
首先,由1号提出分配方案,然后大家表决,当且仅当超过半数的人同意时,按照他的方案
进行分配,否则将被扔进大海喂鲨鱼
如果1号死后,再由2号提出分配方案,然后剩下的4人进行表决,当且仅当超过半数的人同
意时,按照他的方案进行分配,否则将被扔入大海喂鲨鱼
依此类推
条件:每个海盗都是很聪明的人,都能很理智地做出判断,从而做出选择。
问题:第一个海盗提出怎样的分配方案才能使自己的收益最大化?
答案:
2号和3号有积极性让1号死,以便自己得到更多。所以,1号无奈之下,可能只有自己得0,而给2和3各50颗。但事实证明,这种做法依然不可行。为什么呢?
因为我们要先看4号和5号的反应才行。很显然,如果最后只剩下4和5,这无论4提出怎样的方案,5号都会坚决反对。即使4号提出自己要0,而把100颗钻石都给5,5也不会答应――因为5号愿意看到4号死掉。这样,5号最后顺利得到100颗钻石——因此,4的方案绝对无法获得半数以上通过,如果轮到4号分配,4号只有死,只有死!
由此可见,4号绝对不会允许自己来分。他注定是一个弱者中的弱者,他必须同意3号的任
何方案!或者1号2号的
合理方案。可见,如果1号2号死掉了,轮到3号分,3号可以说:
我自己100颗,4号5号0颗,同意的请举手!这时候,4号为了不死,只好举手,而5号暴跳如雷地反对,但是没有用。因为3个人里面有2个人同意啊,通过率66.7%,大于50%!
由此可见,当轮到3号分配的时候,他自己100颗,4和5都是0。因此,4和5不会允许轮到3来分。如果2号能够给4和5一些利益,他们是会同意的。
比如2的分配方案是:98,0,1,1,那么,3的反对无效。4和5都能得到1,比3号来分配的时候只能得到0要好得多,所以他们不得不同意。
由此看来,2号的最大利益是98。1号要收买2号,是不可能的。在这种情况下,1号可以给4号和5号每人2颗,自己收买他们。这样,2号和3号反对是无效的。因此,1号的一种分配方案是:96,0,0,2,2。
这是不是最佳方案呢?再想一想,1号也可以不给4号和5号各2个,而只需要1个就搞定了3号,因为如果轮到2号来分配,2号是可以不给3号的,3号的得益只有0。所以,能得到1个,3号也该很满意了。所以,最后的解应该是:97,0,1,2,0。
好,再倒推。假设1号提出了97,0,1,0,2的方案,1号自己赞成。2和4反对。3∶2,关键就在于3号和5号会不会反对。假设3号反对,杀掉1号,2号来分配,3自己只能得到0。显然,3号不划算,他不会反对。如果5号反对,轮到2号、3号、4号来分配,5号自己
最多只能得到1。
所以,3号和5号与其各得到0和1,还不如现在的1和2。
正确的答案应该是:1号分配,依次是:97,0,1,0,2; 或者是:97,0,1,2,0。
--------------------------------------------------------------------------------
第七题:
有一个村庄有一百个人,每个
人有一条狗并且每个人都有枪,条件是:1。肯定有病狗 2。自己不能看出自己狗有病,只能看出别人的狗有病 3。互相不能交流,就是说看出别人的狗有病你无法让他知道 4。病狗
主人一旦
发现自己的狗是病狗就当天立即打死,而且只能病狗自己的主人能开枪杀。 好了,第一天没有枪响,第二天也没有枪响,第三天听见一阵枪响,请问有几条病狗?
答案:
第一天没枪响,说明每个人至少看到一条病狗,则至少两条;
第二天还没枪响,说明每个人至少看到两条条病狗,则至少三条;
第三天,枪响了,说明有的人只看到有两条,所以知道自己的狗是病狗;
所以是三条。
--------------------------------------------------------------------------------
第八题:
对一批编号为1-100,全部开关朝上(开)的灯进行以下操作:凡是1的倍数反方向拨一次开关;2的倍数反方向又拨一次开关;3的倍数反方向又拨一次开关……问:最后为关熄状态的灯的编号是哪些?
答案:
根据题目我们可以知道,号码为N的灯,拨开关的次数是等于N的约数的个数的。
要想使灯关闭,约数的个数应该是奇数。
而一般来说,任何一个数N都至少有两个约数:即1和N本身。
其他任何一个约数都是一一对应的(例如6的约数中2和3对应)。
也就是说,理论上来讲,每个数的约数的个数都应该是偶数。
只有一种例外的情况,即某数中两个互相对应的约数相等(例如4的约数中2的对应约数也为2)。
这样的数才能有奇数个约数。
也就是说,N必须是某数的平方数。
100以内最大的平方数为100,是10的平方。
最小的平方数为1,是1的平方。
那么100以内的平方数总共只能有10个,即
1^2=1,
2^2=4.
3^2=9
4^2=16
5^2=25
6^2=36
7^2=49
8^2=64
9^2=81
10^2=100
而这些平方数就是所求的编号数。
--------------------------------------------------------------------------------
第九题:
假设排列着100个乒乓球,由两个人轮流拿球装入口袋,能拿到第100个乒乓球的人为胜利者。条件是:每次拿球者至少要拿1个,但最多不能超过5个,问:如果你是最先拿球的人,你该拿几个?以后怎么拿就能保证你能得到第100个乒乓球?
答案:要给对手留6个,这样不管怎么拿你都能拿到最后一个。开始拿4个,后来对方拿X我就拿6-X。
--------------------------------------------------------------------------------
第十题:
S先生、P先生、Q先生他们知道桌子的抽屉里有16张扑克牌:红桃A、Q、4 黑桃J、8、4、2、7、3 草花K、Q、5、4、6 方块A、5。约翰教授从这16张牌中挑出一张牌来,并把这张牌的点数告诉 P先生,把这张牌的花色告诉Q先生。这时,约翰教授问P先生和Q 先生:你们能从已知的点数或花色中推知这张牌是什么牌吗? 于是,S先生听到如下的对话: P先生:我不知道这张牌。Q先生:我知道你不知道这张牌。 P先生:现在我知道这张牌了。 Q先生:我也知道了。 听罢以上的对话,S先生想了一想之后,就正确地推出这张牌是什么牌。 请问:这张牌是什么牌?
答案:
从“P先生:我不知道这张牌”可知,他虽然知道牌的点数,仍无法知道是什么牌,也就是说,这个点数至少有两种花色,所以只可能是A、Q、5、4中的一只;从“Q先生:我知道你不知道这张牌。”可知,Q知道此花色牌的点数只能包括A、Q、4、5中,也就是说,牌的花色只可能是红桃、方块;从“ P先生:现在我知道这张牌了。”知道,P看到的点数在红桃、方块三种花色中是唯一的,也就是说,不可能是A,只可能是Q、4、5。如果此牌点数为A,P先生还是无法判断。从“Q先生:我也知道了。”可知,花色只能是方块。如果是红桃,Q先生排除A后,还是无法判断是Q还是4。 综上所述,这张牌是方块5。
--------------------------------------------------------------------------------
第十一题:
小明和小强都是张老师的学生,张老师的生日是M月N日,2人
都知道张老师的生日是下列10组中的一天,张老师把M值告诉了小明,
把N值告诉了小强,张老师问他们知道他的生日是那一天吗?
3月4日 3月5日 3月8日
6月4日 6月7日
9月1日 9月5日
12月1日 12月2日 12月8日
小明说:如果我不知道的话,小强肯定也不知道
小强说:本来我也不知道,但是现在我知道了
小明说:哦,那我也知道了
请根据以上对话推断出张老师的生日是哪一天?请说明原因。
答案:
1.小明说:如果我不知道的话,小强肯定也不知道
小明能肯定小强不知道,那就说明小强拿到的肯定不是7和2(因为7和2直接可以确定是6月7日和12月2日);
小明能肯定小强拿到的不是7和2,那么他自己拿到的肯定不是6和12
范围变为
3月4日 3月5日 3月8日
9月1日 9月5日
2.小强说:本来我也不知道,但是现在我知道了
当小强知道了小明拿到的是3或者9,他马上就知道了准确日期,所以小强拿到的不可能是5,只能是1,4,8中的一个
范围变为
3月4日 3月8日
9月1日
3.小明说:哦,那我也知道了
小明知道了,我的代码也算出来了
(如果有维一的月份,则小明能确定)
维一的月份是9
所以老师的生日为9月1日。


