RUC_JudgeOnline 1002 矩阵乘法_C/C++_编程开发_程序员俱乐部

矩阵乘法（简单）

Description

N*P阶的矩阵A与P*M阶的矩阵B的乘积C是一个N*M阶的矩阵。C的任何一个元素Cij的值为A的矩阵的第i行和B矩阵的第j列的P个对应元素的乘积之和，即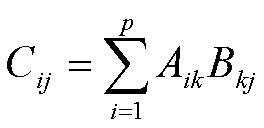



其中p为A矩阵的列数,也是B矩阵的行数,又称为两个相乘矩阵的内阶数。两矩阵相乘的必要条件是内阶数相等。限定2<=i,j,p<=5

Input

输入文件第一行包含3个整数N,P,M(2<=N,P,M<=5),每两个数间有一空格。
接下来的N行,每行P个整数,第i+1行的第j个整数表示A[i][j]的值，每两个数间有一空格。
接下来的P行,每行M个整数,第i+N+1行的第j个整数表示B[i][j]的值，每两个数间有一空格。

Output

输出文件共N行,每行M个整数，每两个数间有一空格。
第i行第j个整数表示C[i][j]的值

Sample Input

?

3 3 3
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1

?

Sample Output

?

3 3 3
3 3 3
3 3 3

?

Source

习题05-03

?

问题分析：

这个题目不是n阶矩阵的算法，所以事实上是相当简单的。只需要好好利用矩阵乘法的原理，用个三重循环即可计算出最终结果。由于题目的规模是相当小的，所以可以直接三重循环。

解决方案：

使用一个sum值，记录每次计算出的乘积。进行一个累加即可算出最终矩阵相乘的结果。具体可见程序实现。

参考程序：

//**********************************
//Author: GWL
//Date: 2010-12-09
//**********************************
#include <stdio.h>
#include <memory.h>
int main()
{
    int N,P,M,sum;
    scanf("%d %d %d",&N,&P,&M);

    if((N>=2&&N<=5)&&(M>=2&&M<=5)&&(P>=2&&P<=5)) //Valiable
    {
        int A[6][6],B[6][6],C[6][6];
        int i,j,k;
        for(i=0;i<N;i++)      //input A
        {
            for(j=0;j<P-1;j++)
            {
                scanf("%d ",&A[i][j]);
            }
            scanf("%d",&A[i][j]);
        }
        for(i=0;i<P;i++)      //input B
        {
            for(j=0;j<M-1;j++)
            {
                scanf("%d ",&B[i][j]);
            }
            scanf("%d",&B[i][j]);
        }
        memset(C,0,sizeof(C));     //init C
        for(i=0;i<N;i++)
             for(k=0;k<P;k++)
                for(j=0;j<M;j++)    //cal C
                {
                    sum=A[i][k]*B[k][j];
                    C[i][j]=C[i][j]+sum;
                 }
        for(i=0;i<N;i++)      //output
        {
             for(j=0;j<M;j++)  
                printf("%d ",C[i][j]);
            printf("\n");
        }  
    }
    return 0;
}

?

?

?

1.输出时候的换行问题

2.对C数组的清空问题