 class="topic_img" alt=""/>
class="topic_img" alt=""/>
英文原文:Beating the binary search algorithm
二分检索是查找有序数组最简单然而最有效的算法之一。现在的问题是,更复杂的算法能不能做的更好?我们先看一下其他方法。
有些情况下,散列整个数据集是不可行的,或者要求既查找位置,又查找数据本身。这个时候,用哈希表就不能实现O(1) 的运行时间了。但对有序数组, 采用分治法通常可以实现O(log (n))的最坏运行时间。
在下结论前,有一点值得注意,那就是可以从很多方面“击败”一个算法:所需的空间,所需的运行时间,对底层数据结构的访问需求。接下来我们做一个运行时对比实验,实验中创建多个不同的随机数组,其元素个数均在 10,000 到 81,920,000 之间,元素均为 4 字节整型数据。
二分检索

二分检索算法的每一步,搜索空间总会减半,因此保证了运行时间。在数组中查找一个特定元素,可以保证在 O(log (n))时间内完成,而且如果找的正好是中间元素就更快了。也就是说,要从 81,920,000 个元素的数组中找某个元素的位置,只需要 27 个甚至更少的迭代。
由于二分检索的随机跳跃性,该算法并非缓存友好的,因此只要搜索空间小于特定值(64 或者更少),一些微调的二分检索算法就会切换回线性检索继续查找。然而,这个最终的空间值是极其架构相关的,因此大部分框架都没有做这个优化。
快速检索;最后回归到二分检索的快速检索

如果由于某些原因,数组长度未知,快速检索可以识别初始的搜索域。这个算法从第一个元素开始,一直加倍搜索域的上界,直到这个上界已经大于待查关键字。之后,根据实现不同,或者采用标准的二分检索查找,或者开始另一轮的快速检索。前者可以保证O(log (n)) 的运行时间,后者则更接近O(n)的运行时间。
如果我们要找的元素比较接近数组的开头,快速检索就非常有效。
抽样检索

抽样检索有点类似二分检索,不过在确定主要搜索区域之前,它会先从数组中拿几个样例。最后,如果范围足够小,就采用标准的二分检索确定待查元素的准确位置。这个理论很有趣,不过在实践中执行效果并不好。
插值检索;最后回归到顺序查找的插值检索

在被测的算法中,插值检索可以说是“最聪明”的一个算法。它类似于人类使用电话簿的方法,它试图通过假设元素在数组中均匀分布,来猜测元素的位置。
首先,它抽样选择出搜索空间的开头和结尾,然后猜测元素的位置。算法一直重复这个步骤,直到找到元素。如果猜测是准确的,比较的次数大概是O(log (log (n)),运行时间大概是O(log (n));但如果猜测的不对,运行时间就会是O(n)了。
插值检索的一个改进版本是,只要可推测我们猜测的元素位置是接近最终位置的,就开始执行顺序查找。相比二分检索,插值检索的每次迭代计算代价都很高,因此在最后一步采用顺序查找,无需猜测元素位置的复杂计算,很容易就可以从很小的区域(大概 10 个元素)中找到最终的元素位置。
围绕插值检索的一大疑问就是,O(log (log (n))的比较次数可能产生O(log (log (n))的运行时间。这并非个案,因为存储访问时间和计算下一次猜测的 CPU 时间相比,这两者之间要有所权衡。如果数据量很大,而且存储访问时间也很显著,比如在一个实际的硬盘上,插值检索轻松击败二分检索。然而,实验表明,如果访问时间很短,比如说 RAM,插值检索可能不会产生任何好处。
试验结果
试验中的源代码都是用 Java 写的;每个实验在相同的数组上运行 10 次;数组是随机产生的整型数组,存储在内存中。
在插值检索中,首先会采用抽样检索,从检索空间拿 20 个样例,以确定接下来的搜索域。如果假定的域只有 10 个或更少的元素,就开始采用线性检索。另外,如果这个搜索域元素个数小于 2000,就回退到标准的二分检索了。
作为参考,java 默认的 Arrays.binarySearch 算法也被加入实验,以同自定义的算法对比运行时间。
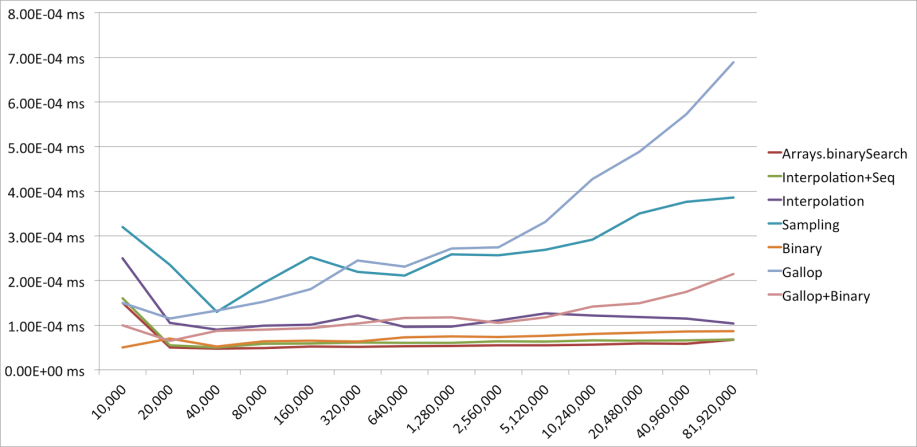

尽管我们对插值检索期望很高,它的实际运行时间并未击败 java 默认的二分检索算法。如果存储访问时间长,结合采用某些类型的哈希树和B+ 树可能是一个更好的选择。但值得注意的是,对均匀分布的数组,组合使用插值检索和顺序检索在比较次数上总能胜过二分检索。不过平台的二分检索已经很高效,所以很多情况下,可能不需要用更复杂的算法来代替它。
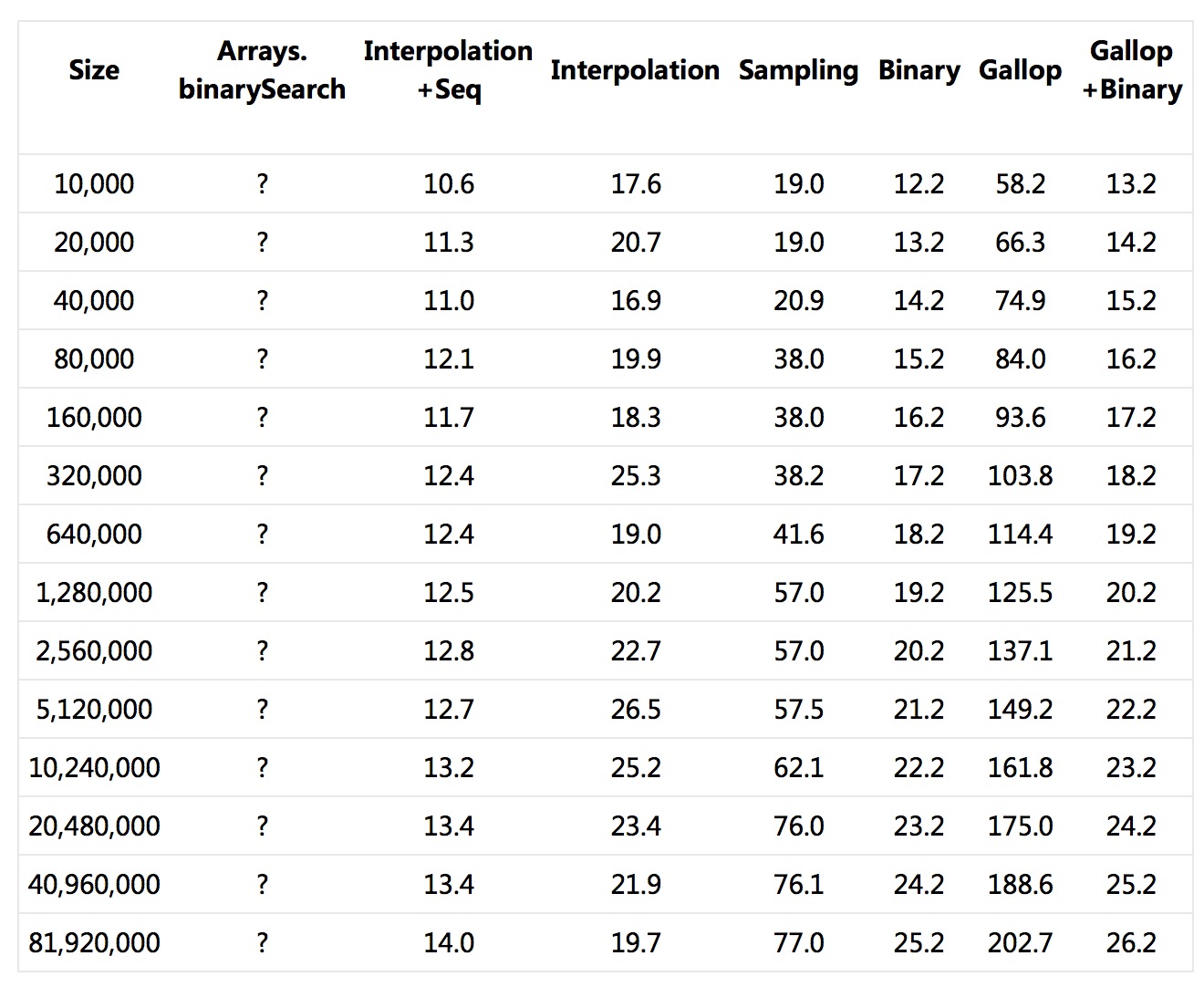
原始数据 – 每个检索的平均运行时间

原始数据 – 每个检索的平均比较次数
源代码
点此获取检索算法的完整源代码。注意,代码不是产品级别的;比如,在某些例子里,可能有过多或过少的范围检查。
翻译: 伯乐在线 - hf_cherish
译文链接: http://blog.jobbole.com/73517/