上期我们用了很多篇幅谈论三角函数,但是说三角函数怎么好意思不提那套著名的傅里叶变换图呢?
所以:
变身吧傅里叶
不,不是变成夜礼服。

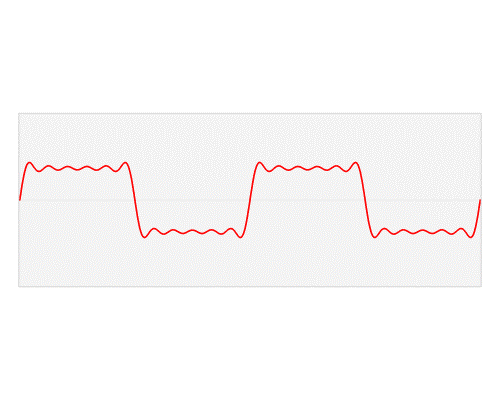
图片作者:LucasVB
和某些公然嘲笑应用的数学家不同,傅里叶特别重视应用领域,而他的傅里叶变换也不负众望成了工程和物理领域里最重要的数学公式之一。
这里展示的傅里叶变换(的三角函数形式)的基本原理是,多个正余弦波叠加(蓝色)可以用来近似任何一个原始的周期函数(红色)。这样近似的效果有点像称量的砝码:不管你原物的质量多奇怪,我总能化归成“5 个 1 斤砝码、3 个 1 两砝码”这样几个基本单位之和。上图末尾处蓝色的竖线就可以想象成“我用了 5 个 1 号波、3 个 2 号波”等等。这在计算上多省事儿、处理上多方便就不用说了……
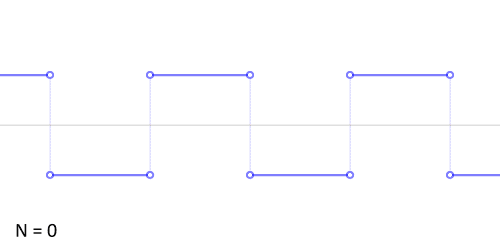
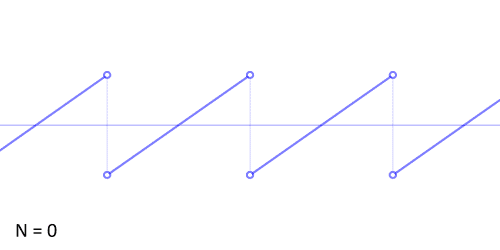

几个傅里叶分解实例,用波叠加出分段函数。图片作者:LucasVB
当然傅里叶分解的好处和用法远不止这些,但那就是一本书的篇幅了。打住。
如果你还记得酷炫动图(三)中讨论过的圆和三角函数之间的密切联系,那你也能看懂下面这张图:
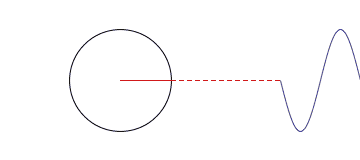
图片作者:Matthew Henderson
大地上的河流

图片来源:google
图片作者可能是 blog.matthen.com
Hello?走错片场了吧?标题写的是数学啊?
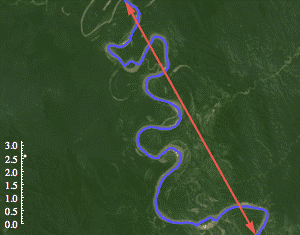
没有错,这是数学里诸多脑洞大开的定理之一:平原上的河流,从源头到出海口的干流总长度(蓝线)和源头到出海口之间的直线距离(红线)的比值,平均而言比 3 大一点儿。更准确地说,这个比值应当趋近于π。
图中所示是秘鲁艾尔·西拉保护区里的一条河流,虽然因为地形和时间尺度原因,其比值更接近于 2.5,不过意思大家已经看到了。
但是这真的是数学!因为河流的自组织过程很容易形成分形。
一条完美的笔直河流是平衡的,但这是不稳定的平衡。现实中的河流总会因为各种原因而有所弯曲,一旦河道打弯,弯道内侧和外侧的水流速度就会出现差异,外侧遭到冲刷,而内侧则发生沉积。久而久之弯曲会越来越大,最终河道裁弯取直形成牛轭湖,开始新的循环。
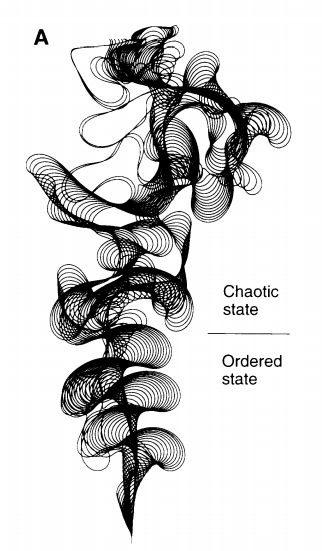
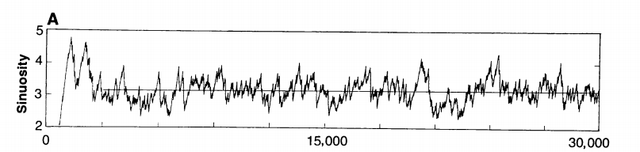
而 1996 年《科学》上的一篇论文认为,对于平原上的河流,这一过程的临界态是可以用分形来描述的。下面两张图是作者汉斯-亨里克·斯托罗姆(Hans-Henrik Stolum)用纯粹的数学公式推演出来的河流演化,可以和上图对比一下。
无限的黄金(率)
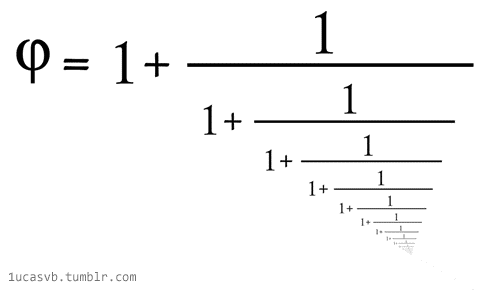
图片作者:LucasVB
这个φ不是别的,就是黄金分割率那个 1.618 了。当然如果你喜欢 0.618,把前面的 1 去掉就是。
常用的黄金分割表达方式是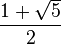
,但是有一个有趣的连分数表达式,就是上面那张停不下来的动图。
当然实际中我们没法无穷地这么除下去……用这个连分数迭代来近似黄金比例的话,误差程度是:
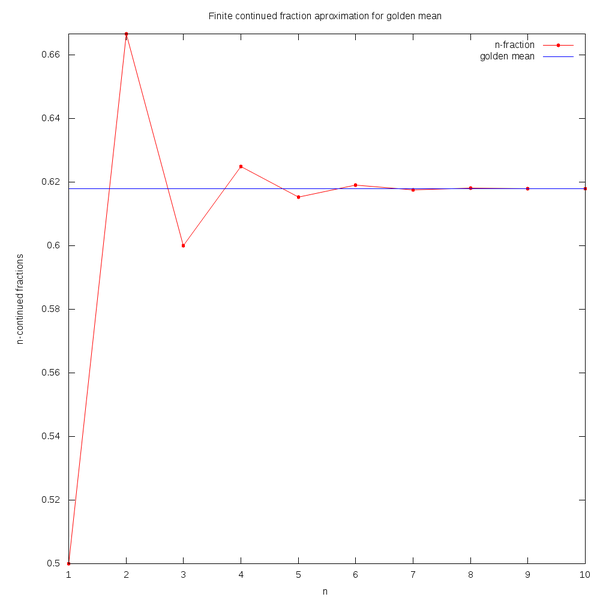
图片来源:wikipedia
还不错嘛。
为什么这个连分数无限迭代下去可以用来算黄金率?注意它的格式:x = 1 + 1/x
而黄金率的定义你还记得吗?在下图中,如果 (a + b)/a = a/b ,那么这个比值就是黄金律。
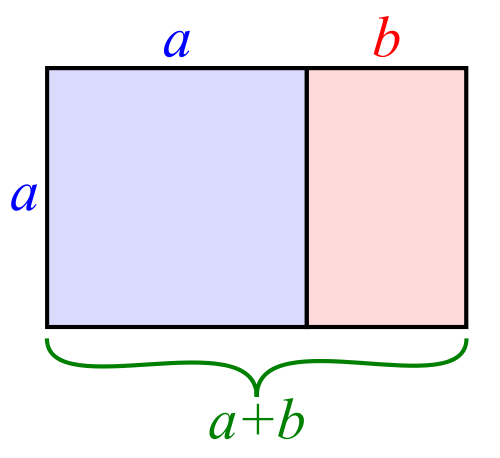
图片来源:wikipedia
如果我们令 a/b = φ,那么上式就立刻化简成了
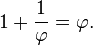
如果你学过相关的迭代法求近似解理论,现在应该已经在颔首微笑了。如果没有,那么想着“这两个式子形式完全一样肯定有什么关联”就好……
扩展阅读
本期的动图大部分依然来自 LucasVB,不过也出现了 blog.matthen.com,下期他的戏份会更多。