今天主要讲到的是决策树算法,这是一种非常经典的分类算法,经过数据集的训练,能够高效的判断出一个数据项所属的类别。
决策树算法是一种有监督的学习,也就是说会事先给定一定类别和数据集合。通过学习,能够判定出进来数据所属的类。当然,很多聚类算法都是无监督学习的,我们以后再进行讨论。顾名思义,决策树是一颗树形的数据结构,决策树可以是多叉树也可以hashu.html" target="_blank">二叉树。决策树实际上是一种基于贪心策略构造的,每次选择的都是最优的属性进行分裂。常用的决策树算法有ID3,C4.5。其实这两种算法本质上是一样的,并且他们几乎实在同一时间独立发现的。ID3此算法的目的在于减少树的深度。但是忽略了叶子数目的研究。C4.5算法在ID3的基础上进行了改进,对于预测变量的缺值处理、剪枝技术、派生规则等方面作了较大改进,既适合于分类问题,又适合于回归问题。有时决策树也会有剪枝方面的考虑,这主要从性能、噪声、效率的角度考虑。
算法的基本思想可以概括为:
1)树以代表训练样本的根结点开始。 2)如果样本都在同一个类.则该结点成为树叶,并记录该类。 3)否则,算法选择最有分类能力的属性作为决策树的当前结点. 4 )根据当前决策结点属性取值的不同,将训练样本根据该属性的值分为若干子集,每个取值形成一个分枝,有几个取值形成几个分枝。匀针对上一步得到的一个子集,重复进行先前步骤,递归形成每个划分样本上的决策树。一旦一个属性只出现在一个结点上,就不必在该结点的任何后代考虑它,直接标记类别。 5)递归划分步骤仅当下列条件之一成立时停止: ①给定结点的所有样本属于同一类。 ②没有剩余属性可以用来进一步划分样本.在这种情况下.使用多数表决,将给定的结点转换成树叶,并以样本中元组个数最多的类别作为类别标记,同时也可以存放该结点样本的类别分布[这个主要可以用来剪枝]。 ③如果某一分枝tc,没有满足该分支中已有分类的样本,则以样本的多数类生成叶子节点。 算法中2)步所指的最优分类能力的属性。这个属性的选择是本算法种的关键点,分裂属性的选择直接关系到此算法的优劣。 一般来说可以用比较信息增益和信息增益率的方式来进行。 其中信息增益的概念又会牵扯出熵的概念。熵的概念是香农在研究信息量方面的提出的。它的计算公式是: Info(D)=-p1log(p1)/log(2.0)-p2log(p2)/log(2.0)-p3log(p3)/log(2.0)+...-pNlog(pN)/log(2.0) (其中N表示所有的不同类别)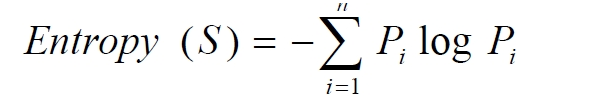 而信息增益为:
Gain(A)=Info(D)-Info(Da) 其中Info(Da)数据集在属性A的情况下的信息量(熵)。
而信息增益为:
Gain(A)=Info(D)-Info(Da) 其中Info(Da)数据集在属性A的情况下的信息量(熵)。
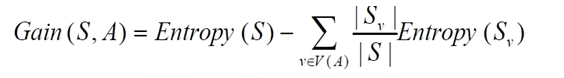 我以下实现的算法能够处理任意维度的属性和任意个不同类别的数据量。
数据格式为:
数据属性头
数据项
算法能够一行行读txt数据,当然其他格式数据也是可以的,稍微改动下void InitDataSet();方法即可。相当方便实用。本着开源的方式,附上90%代码:void InitDataSet();方法代码没有附上,如果需要全部源代码请点赞后留下email地址,我将会在第一时间发到你邮箱!不便之处请原谅,毕竟写一篇文章也不是那么容易,我只是想看看到底能帮助到多少人。谢谢理解!
我以下实现的算法能够处理任意维度的属性和任意个不同类别的数据量。
数据格式为:
数据属性头
数据项
算法能够一行行读txt数据,当然其他格式数据也是可以的,稍微改动下void InitDataSet();方法即可。相当方便实用。本着开源的方式,附上90%代码:void InitDataSet();方法代码没有附上,如果需要全部源代码请点赞后留下email地址,我将会在第一时间发到你邮箱!不便之处请原谅,毕竟写一篇文章也不是那么容易,我只是想看看到底能帮助到多少人。谢谢理解!
1 #include<iostream>
2 #include<fstream>
3 #include<math.h>
4 #include<vector>
5 #include<string>
6 #include<map>
7 #include<sstream>
8 using namespace std;
9 vector< vector<string> > AllObject;//加载所有训练数据
10 vector<string> object;//数据项,即行记录
11 vector<string> AttributeList;//属性列表
12 map<string,vector<string>> mapAttribute_Values;//各属性对应的值,用map保存
13 vector<string> classList;//分类列表,即一共有多少类别保存下来
14 int objectCount;//训练数据量
15 int attributeCount;//属性量
16 int classCount;//类别量
17 struct Node{//决策树数据结构
18 string currentAttribute;//是什么属性
19 string attributeValue;//当前属性值
20 string belongClass;//属于什么类型
21 vector<Node *> childs;//孩子节点有哪些
22 Node(){
23 currentAttribute="";
24 attributeValue="";
25 belongClass="";
26 }
27 };
28 void InitDataSet();//用来加载数据,初始化相关变量
29 void buildMapAttribute_Values();//初始化mapAttribute_Values
30 double computeInfo(vector< vector<string> > remainObject,string attributename,string attributvalue,bool ifParent);//计算该attributename保存的信息量
31 double computeGain(vector< vector<string> > remainObject,string attributename);//计算增益信息量,即info(remainObject)-INFO(attributename)
32 int findAttributeRow(string attributeName);//根据属性名称找到该属性在数据项的哪一列
33 bool allAreSameClass(vector< vector<string> > remainObject,string className);//判断所有数据是否都属于className类别
34 string getMostClass(vector< vector<string> > remainObject);//得到remainObject中大多数类别,并返回
35 Node *buildDescideTree(Node *p,vector<string> remainAttribute,vector< vector<string> > remainObject);//构造一颗决策树,
36 void printDecisionTree(Node *p,int i);//输出决策树
37 string getClass(vector<string> item,Node *p);//给定某一数据项item,根据决策树返回其类别。
38 int main(){
39 vector<int> x(5,0);
40 InitDataSet();
41 Node *p=new Node();
42 p->currentAttribute="root";
43 p=buildDescideTree(p,AttributeList,AllObject);
44 printDecisionTree(p,0);
45 vector<string> item;
46 while(true){
47 string x;
48 int i=0;
49 for (int i=0;i<attributeCount;i++)
50 {
51 cin>>x;
52 item.push_back(x);
53 }
54 cout<<"类别是:"<<getClass(item,p)<<endl;
55 item.erase(item.begin(),item.end());
56 }
57 system("pause");
58 }
59 void printDecisionTree(Node *p,int depth){//p决策树指针,depth表示当前走过的深度
60 if (p->attributeValue!=""){
61 for (int i=0;i<depth;i++){//深度为多少则在前面空多少格,便于美观
62 cout<<'\t';
63 }
64 cout<<p->attributeValue<<" "<<endl;
65 for (int i=0;i<depth+1;i++){//
66 cout<<'\t';
67 }
68 }
69 if (p->currentAttribute!=""){
70 cout<<p->currentAttribute<<" "<<endl;
71 }
72
73 if (p->belongClass!=""){
74 cout<<"类别是"<<p->belongClass<<" "<<endl;
75 }
76 for (size_t i=0;i!=p->childs.size();i++){
77 printDecisionTree(p->childs[i],depth+1);//递归输出
78 }
79 }
80 string getClass(vector<string> item,Node *p){
81 while (p->childs.size()!=0){//从根节点出发,一直找到叶子节点,同时返回className。若没有孩子节点,直接返回className
82 string attributeName=p->currentAttribute;
83 int attributeRow=findAttributeRow(attributeName);
84 string attributeValue=item[attributeRow];
85 for (size_t i=0;i!=p->childs.size();i++){//寻找到决策树中属性值与item属性值相同的节点,并往下一层寻找
86 if (!attributeValue.compare((p->childs[i])->attributeValue)){
87 p=p->childs[i];//找到之后就break
88 break;
89 }
90 }
91 }
92 return p->belongClass;
93 }
94 //计算信息量,熵
95 double computeInfo(vector< vector<string> > remainObject,string attributename,string attributevalue,bool ifParent){
96 vector<int> perValueCount(classCount,0);//保存每个值在remainObject出现的次数,便于计算概率
97 int attributeAllowRow=findAttributeRow(attributename);
98 for (size_t i=0;i!=remainObject.size();i++){//得到该属性时,数据项中各个分类的情况
99 for (size_t j=0;j!=classCount;j++){
100 if (ifParent&&!remainObject[i][attributeCount].compare(classList[j])){
101 perValueCount[j]++;
102 }
103 else if (!ifParent&&!remainObject[i][attributeAllowRow].compare(attributevalue)&&!remainObject[i][attributeCount].compare(classList[j])){
104 perValueCount[j]++;
105 }
106 }
107 }
108 double sumObject=0;//保存出现当前属性值的总项
109 for (int i=0;i<classCount;i++){
110 sumObject+=perValueCount[i];
111 }
112 double info=0;
113 for (int i=0;i<classCount;i++){
114 double ratio=(double)perValueCount[i]/(double)sumObject;
115 if (ratio){//概率为0时忽视它
116 info+=(-(ratio)*(log(ratio)/log(2.0)));//根据-p1log(p1)-p2log(p2)....计算出他的总信息量,也就是熵
117 }
118 }
119 return info;
120 }
121 double computeGain(vector< vector<string> > remainObject,string attributename){//计算信息增益,attributename表示属性名称
122 double parentInfo=computeInfo(remainObject,attributename,"",true);//首先计算当前属性的父信息量
123 double childInfo=0;//保存该属性各值的熵,
124 vector<string> attributeValueList=mapAttribute_Values[attributename];
125 vector<int> perValueCount(attributeValueList.size(),0);//保存该属性各个值的object个数
126 int attributeAllowRow=findAttributeRow(attributename);
127 for(size_t i=0;i<remainObject.size();i++){//得到为该属性时,各值的个数
128 for(size_t j=0;j<attributeValueList.size();j++){
129 int temp=0;
130 if (!remainObject[i][attributeAllowRow].compare(attributeValueList[j])){
131 perValueCount[j]++;
132 break;
133 }
134 }
135 }
136 double getOneChildInfo;
137 for(size_t i=0;i!=attributeValueList.size();i++){
138 getOneChildInfo=computeInfo(remainObject,attributename,attributeValueList[i],false);//计算该属性各个值的信息
139 childInfo+=((double)perValueCount[i]/(double)remainObject.size())*getOneChildInfo;
140 }
141 return (parentInfo-childInfo);//返回信息增益
142 }
143 int findAttributeRow(string attributeName){//返回属性所在的列
144 for (int i=0;i<attributeCount;i++)
145 {
146 if (!AttributeList[i].compare(attributeName))
147 {
148 return i;
149 }
150 }
151 return -1;
152 }
153 Node *buildDescideTree(Node *p,vector<string> remainAttribute,vector< vector<string> > remainObject){
154 if(p==NULL)
155 p=new Node();
156 for(int i=0;i<classCount;i++){//若所有的都是同一类,则直接返回。
157 if(allAreSameClass(remainObject,classList[i])){
158 p->belongClass=classList[i];
159 return p;
160 }
161 }
162 if(0==remainAttribute.size()){//返回最多的那一项
163 p->belongClass=getMostClass(remainObject);
164 return p;
165 }
166 double maxGain=0,currentGain;
167 string attributeName;
168 for(size_t i=0;i!=remainAttribute.size();i++){//信息增益最大的最为分裂点
169 currentGain=computeGain(remainObject,remainAttribute[i]);
170 if (currentGain>maxGain){
171 maxGain=currentGain;
172 attributeName=remainAttribute[i];
173 }
174 }
175 p->currentAttribute=attributeName;
176 int attributeRow=findAttributeRow(attributeName);
177 vector<string> newRemainAttribute;//剩下的属性
178 for (size_t i=0;i!=remainAttribute.size();i++){
179 if (remainAttribute[i].compare(attributeName)){
180 newRemainAttribute.push_back(remainAttribute[i]);
181 }
182 }
183 vector< vector<string> > newRemainObject;//剩余的数据项
184 vector<string> attributeValues=mapAttribute_Values[attributeName];
185 for (size_t i=0;i!=attributeValues.size();i++){
186 for(size_t j=0;j!=remainObject.size();j++){
187 if(!remainObject[j][attributeRow].compare(attributeValues[i]))
188 newRemainObject.push_back(remainObject[j]);
189 }
190 Node* q=new Node();
191 q->attributeValue=attributeValues[i];
192 int mm=newRemainObject.size();
193 if (newRemainObject.size()>0){//若该属性的这个值不存在object,则返回该属性中最多的项。否则继续递归计算
194 buildDescideTree(q,newRemainAttribute,newRemainObject);
195 }else{
196 p->belongClass=getMostClass(remainObject);
197 }
198 p->childs.push_back(q);
199 newRemainObject.erase(newRemainObject.begin(),newRemainObject.end());
200 }
201 return p;
202 }
203 bool allAreSameClass(vector< vector<string> > remainObject,string className){//判断是否都属于同一类
204 for (size_t i=0;i!=remainObject.size();i++)
205 {
206 if (remainObject[i][attributeCount].compare(className)){
207 return false;
208 }
209 }
210 return true;
211 }
212 string getMostClass(vector< vector<string> > remainObject){//返回类最多的
213 string attributeName;
214 vector<int> perCount(classCount,0);//用来保存各个类别中他们有的数据项object
215 for (size_t i=0;i!=remainObject.size();i++){
216 for (int j=0;j<classCount;j++){
217 if (!remainObject[i][classCount].compare(classList[j])){
218 perCount[j]++;//
219 }
220 }
221 }
222 int maxNum=-1,classRow=-1;
223 for (size_t i=0;i!=classCount;i++){
224 if (perCount[i]>maxNum){
225 maxNum=perCount[i];
226 classRow=i;
227 }
228 }
229 return classList[classRow];//返回用用最多项的那个属性
230 }
231 273 void buildMapAttribute_Values(){
274 for(int attributerow=0;attributerow<attributeCount;attributerow++){
275 string currentAttribute=AttributeList[attributerow];
276 vector<string> attributeValue;
277 bool exit=false;
278 for(int objectColumn=0;objectColumn<objectCount;objectColumn++){
279 string currentAttributeValue=AllObject[objectColumn][attributerow];
280 for(size_t i=0;i<attributeValue.size();i++){
281 if(!currentAttributeValue.compare(attributeValue[i])){
282 exit=true;
283 break;
284 }
285 }
286 if(!exit)
287 attributeValue.push_back(currentAttributeValue);
288 exit=false;
289 }
290 mapAttribute_Values[currentAttribute]=attributeValue;
291 attributeValue.erase(attributeValue.begin(),attributeValue.end());
292 }
293 }
本算法测试了两个数据集,都是从网上搜集过来的,运行效果和准确率都是杠杠的。附上数据集。

[dataset1]

[dataset2]
算法运行后,我打印了决策树的组成,便于大家对决策树有一个更好的理解:

[dataset1决策树]

[dataset2决策树]
版权所有,欢迎转载,但是转载请注明出处:潇一