在《美国队长2》影片中,美国队长不背降落伞便跳出了机舱并落到了水里。显然我不会玩这一手——但这一手是不是可行的呢?别忘了,美国队长的超能力无非是成为最强壮的凡夫俗子。他并没有超人的力量。
他落水时速度有多大?
美国队长跳出机舱之后,采用的便是跳伞运动员的标准自由落体姿态。在这种姿态下,他很快就会达到极限速度,这时向上的空气阻力在数值上等于向下的重力。对于采用这种姿态的普通跳伞运动员,我一直把极限速度设为大约 120 英里/小时(53.6 米/秒),因此我们就假设这是他下落时的速度。
但是等一下!在自由下落的最后,他改变了姿态,好让脚先触水。
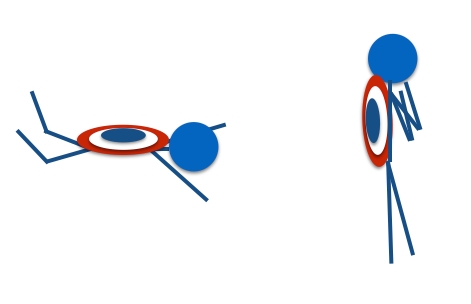
美国队长的跳伞姿态(左)和入水姿态(右)
在第二种姿态下,他的横截面积减小,因而降低了空气阻力。这意味着他会再次加速。我不打算估算站立姿态的横截面积以及阻力系数,而是直接使用这个网站的数据——站立姿态下的极限速度是大约 170 英里/小时(76 米/秒)。
但是他有时间到达新的极限速度吗?让我们假设他以 53.6 米/秒的速度进入站立姿态。我根据视频粗略的估计是入水之前他采用这个姿态大约 4 秒。
如果他确实到达了站立姿态的极限速度,那么下列等式将成立:
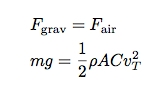
因为我知道这个极限速度是多少,我便能够求出ρAC 的值(ρ是空气密度)。我还需要一个数据——美国队长的质量。我要假设是 90 千克。那么式子将变形为:
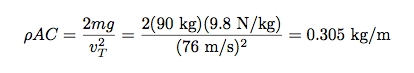
这时我就可以利用这个值来为美国队长改变姿态后的速度建模。由于空气阻力取决于他的速率,最简单的办法就是建立数值模型来计算他在这 4 秒之内的速度。
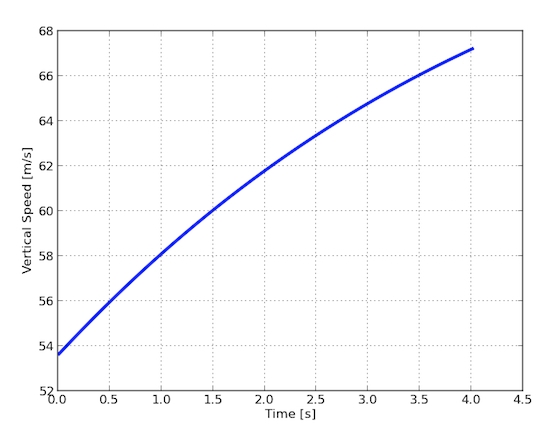
这样算出来他的入水速度是 67.2 米/秒。哦,是的——他中间确实翻了个身,但是我不予考虑。他就是在耍帅而已。
水中减速
下面来看水下的部分。这部分的估算相当困难。以极高速度运动的人体和水的相互作用,与在天空中下落时可不是一回事。不过我会尽量去算。
我会使用与在空气中同样的模型来计算阻力,只不过水的密度要大得多(空气密度是 1.2 千克/立方米,水的密度是 1000 千克/立方米)。如果我假设美国队长在水中和空气中的阻力系数和横截面积都一样,那么我得到的 AC 值是 0.255 平方米(根据站立姿态极限速度)。
他只有一部分身体在水中的难缠阶段我就忽略不计了。下面我可以回到我的数值模型,仅仅修改一下密度。下图是他以 67.2 米/秒的速度入水后速度与时间的关系。
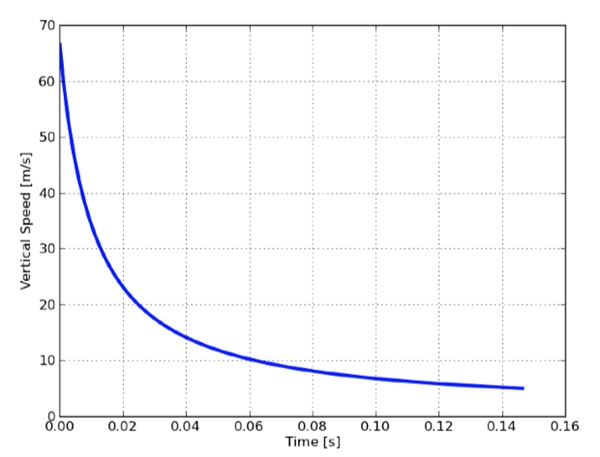
我仅仅绘制出了他的速度降到 5 米/秒之前的情况。说实话,我关注的只是最初的加速度。不过,我刚刚意识到我忽略了浮力——我觉得这倒也没什么,因为这只是一次估算,而且有那么多的气泡,浮力也不太可能会符合普通模型。
看一看最初 0.01 秒的运动,美国队长的速度从 67.2 米/秒降到了 34.2 米/秒。使用 0.01 秒的时长,我们得出平均加速度是……3300 米/秒2,或者 337G。
这是不是太大了?
根据维基百科上关于加速度承受能力的词条,人类可以在极短时间内挺过 100G 的加速度。这确实是极短的时间,但是 337G 的加速度比 100G 高很多——我想我该补充一句,记录中人类幸存下来的最大加速度是 214G。
不过别忘了,这可是美.国.队.长。
