?
?????? 分形是什么?查百度百科,第一句话是——分形,具有以非整数维形式充填空间的形态特征。头有点晕了吧,没关系,这是数学家研究的是,我们只要知道就行,不知道也可以。因为我们关注的不是这个,我们关注的是怎样用编程语言去实现那些美丽的分形图。
????? 先来看看几张分形图片:

?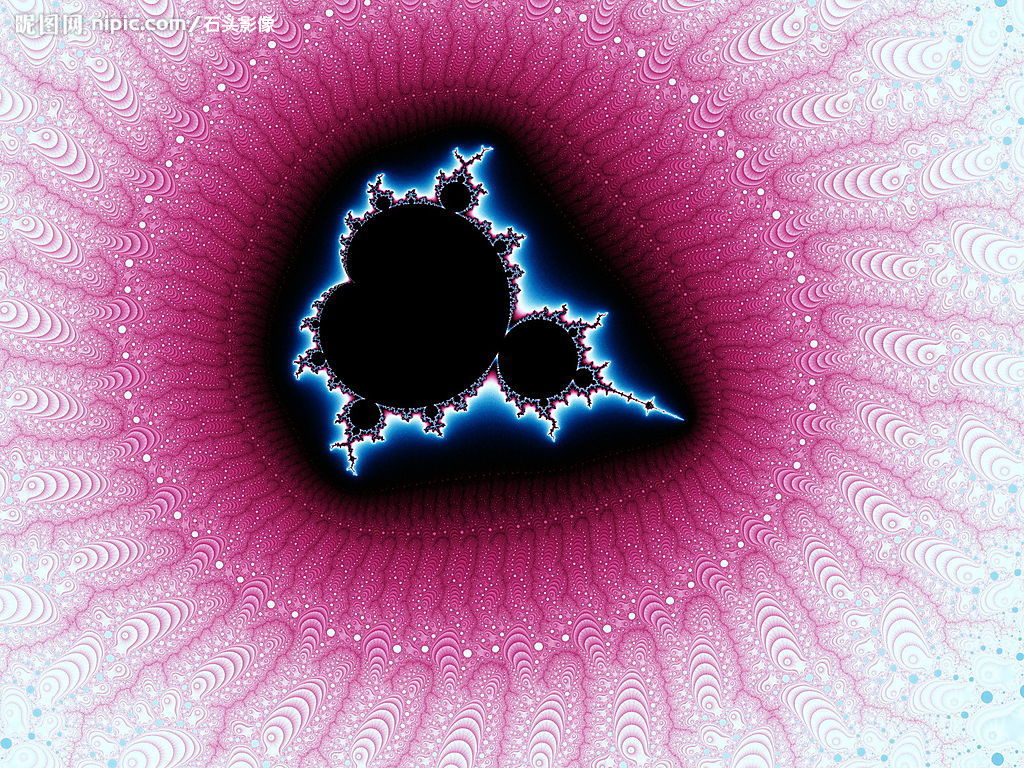
?????? 很漂亮吧,同时也看起来很复杂。你可能会想,编程怎么可能画出这么美丽而又复杂的图片。别怕,这些图片其实并没有你想的那么复杂,仔细观察,我们可以发现这些图形的局部和整体完全是相似的,也就是说我们只要能将局部画出来,整体也就能画出来。
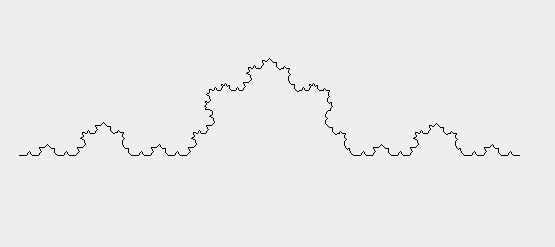
????? 这时候,递归函数就派上大用场了。例如下面这个图形:
?
????? 这个曲线还有个名字,Koch曲线。这个看起来相对简单一点。
????? 它的最基本的图形是这个样子的:

??????
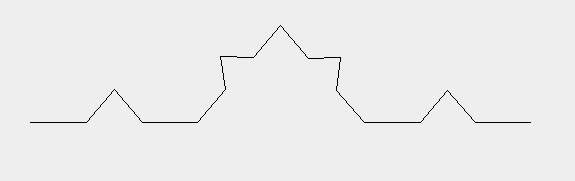
????? 复杂一点:
?
????? 怎样,看出规律了吧。只要在每段线找两个1/3点,再根据这两个点画一个等边三角形,当然得少画一条边,尖角的朝向也得正确,按照这个方法一直画下去就是Koch曲线了。我们现在知道了它最基本的图形,然后又知道了它的演变规律,接下来的事就只剩敲代码了。代码如下:
class="java">import java.awt.Color;
import java.awt.Graphics;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
public class Koch implements ActionListener{
private Graphics g;
//传入画布
public Koch(Graphics g){
this.g = g;
}
//画Koch曲线,参数为起点和终点,n为递归次数
public void draw(int xn,int yn,int xm,int ym,int n){
int x1,y1,x2,y2,x0,y0,x3,y3;//对一条线段画下一层所需的中间三个点和中点
//当达到一定的递归次数,结束
if(n<=0){
g.drawLine(xn, yn, xm, ym);
return;
}
//各点之间的关系
x2 = xm+(xn-xm)/3;
y2 = ym+(yn-ym)/3;
x1 = xm+2*(xn-xm)/3;
y1 = ym+2*(yn-ym)/3;
x0 = (x1+x2)/2;
y0 = (y1+y2)/2;
x3 = (int) ((Math.sqrt(3)/3)*(y2-y1)+x0);
y3 = (int) ((Math.sqrt(3)/3)*(x1-x2)+y0);
--n;
//调用本身,下面参数的点的次序不能乱,不然画的曲线可能会很难看
draw(x2, y2,xm, ym, n);
draw(xn, yn,x1, y1, n);
draw(x1, y1, x3, y3,n);
draw( x3, y3,x2, y2,n);
}
@Override
public void actionPerformed(ActionEvent e) {
draw(100,400,600,400,2);
}
}
?
?
????? 有些图形得用其它方法实现,有些图形的画图公式已经被数学家找出来了,我们也可以直接用。当然主要思想离不开重复、循环。
????? 例如下面的Mandelbrot:

?
代码:
import java.awt.Graphics;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.awt.image.BufferedImage;
import java.awt.image.ImageObserver;
public class Mandelbrot implements ActionListener{
private Graphics g;
//重载构造函数,传入画板对象
public Mandelbrot(Graphics g){
this.g = g;
}
@Override
public void actionPerformed(ActionEvent e) {
double scale = 200; //放大比例
int imax = 570;
int x,y;//当前点
double px = 2, py = 1;//初始点
double x0, y0, xn, yn, xm, ym;
//遍历整个画图区域
for(x=0;x<600;x++){
for(y=0;y<400;y++){
x0 = x/scale - px;
y0 = y/scale - py;
xn = 0;
yn = 0;
int i = 0;
//检测改点是否在Mandelbrot区域内
while( xn*xn + yn*yn < 4 && i < imax ){
xm = (xn+yn)*(xn-yn)+x0;
ym = 2.0*xn*yn+y0;
xn = xm;
yn = ym;
i++;
}
if(i == imax){
//画点,后面加的数只是为了调整位置
g.drawLine(x+100, y+100, x+100, y+100);
}
}
}
}
}
?
?????? 我们还可以为这些图加上颜色:

??????
??????怎样,漂亮吧。分形一下子让我们就让我们这些整天对着电脑的屌丝变的很有艺术气息了,有木有啊!