分形_JAVA_程序员俱乐部

您所在的位置：程序员俱乐部 > 编程开发 > JAVA > 分形

分形

2013/11/30 12:19:01 wuyongzheng 程序员俱乐部我要评论(0)

摘要：学了这么久的java语言，终于进入到了一个比较好玩的环节了，就是分形。起初听说分形根本就对分形没有任何概念，担当逐渐的深入了解，则发现其有趣之处则是可以凭借自己的想象，来实现各种各样有意思的图形。在开始，先看看一些有意思的图形吧。。分形的实现主要是通过迭代，以及递归调用来实现的。(1)迭代使用迭代算法是需要注意三方面的内容：一：要给算法一个退出语句，否则程序会一直迭代下去，导致栈溢出二：要声明至少一个迭代变量三：要给出迭代关系，即迭代变量如何从旧值转变成新值的下面给出的是费波拉契数列的实现1
标签：

    学了这么久的java语言，终于进入到了一个比较好玩的环节了，就是分形。
     起初听说分形根本就对分形没有任何概念，担当逐渐的深入了解，则发现其有趣之处则是可以凭借自己的想象，来实现各种各样有意思的图形。
     在开始，先看看一些有意思的图形吧。。

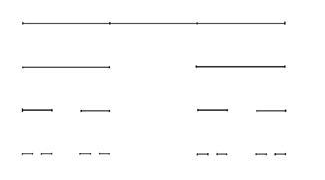
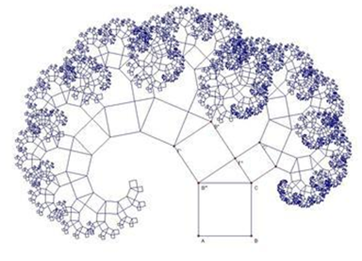
   分形的实现主要是通过迭代，以及递归调用来实现的。
    (1)迭代
    使用迭代算法是需要注意三方面的内容：
     一：要给算法一个退出语句，否则程序会一直迭代下去，导致栈溢出
     二：要声明至少一个迭代变量
     三：要给出迭代关系，即迭代变量如何从旧值转变成新值的
下面给出的是费波拉契数列的实现

class="java">
1.int Fibs(int n) {     
2.   if(n < 0) {     
3.    throw new IllegalArgumentException(" the parameter is valid!");     
4.    }     
5.    int n1 = 0;//F(n-2)，迭代变量  
6.    int n2 = 1;//F(n-1)，迭代变量  
7.    int r = n1;//F(n)     
8.    if(n == 1) {     
9.        r = n2;     
10.    }     
11.    for (int i = 2; i <= n; i++) {   //用循环控制迭代过程  
12.       //迭代关系式  
13.        r = n1 + n2 ;//F(n)=F(n-1)+F(n-2)     
14.        n1 = n2;     
15.        n2 = r;     
16.    }     
17.    return r;     
18.}

（2）递归
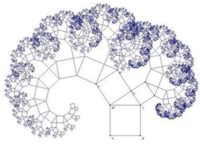
   所谓递归，就是函数调用本身的算法。实际上我们所说的分形中大部分的图形都是利用递归来实现的，如上面的谢尔宾斯三角，毕达哥拉斯树等，都是函数不断地调用自身实现的。递归调用也需要注意不要忘记给函数一个退出的语句，否则函数会一直递归调用下去。

   下面的是代码示例：

public void draw(int x1,int y1,int x2,int y2,int n){
		if(n<=0){
			return;
		}
		
		
		g.drawLine(x1, y1, x2, y2);
		
		//得到新的点的坐标
		int xx1 = x1;
		int xx2 = x1+(x2-x1)/3;
		int xx3 = x1 + 2*(x2 - x1)/3 ;
		int xx4 = x2;
		int yy1 = y1 + 20;
		int yy2 = y2 + 20;
		int yy3 = y1 + 20;
		int yy4 = y2 + 20;
		
		draw(xx1,yy1,xx2,yy2,n -1);//绘制左边的直线
		
		try {
			Thread.sleep(1000);
		} catch (InterruptedException e) {
			// TODO Auto-generated catch block
			e.printStackTrace();
		}
	
		draw(xx3,yy3,xx4,yy4,n -1);//绘制右边的直线
		
		try {
			Thread.sleep(1000);
		} catch (InterruptedException e) {
			// TODO Auto-generated catch block
			e.printStackTrace();
		}

其运行结果：

    其思路很简单，就是先实现简单的一条直线，在分析其后的直线会遵从一个什么样的规律来实现，在调用自身来有规律的实现想要的图形。
     下面在再给出大家毕达哥拉斯树的代码吧！！

 public void Show(double x0,double y0,double l,double a,double b,double c,double count,Graphics g){
double x2;
double y2;
double x3;
double y3;
double x4;
double y4;
double x5;
double y5;
if(count<1)
{
 return;
}//判断是否继续进行递归调用，注意：判断一定要放在递归调用之前，否则这段代码将永远不会被执行
x2 = x0 - l*Math.cos(a);
 y2 = y0 - l*Math.sin(a);
x3 = x2 - l*Math.cos(b);
y3 = y2 - l*Math.sin(b);
x4 = x0 - l*Math.cos(b);
y4 = y0 - l*Math.sin(b);
x5 = x2 - l*Math.cos(Math.PI/6)*Math.cos(c);
y5 = y2 - l*Math.cos(Math.PI/6)*Math.sin(c);

//计算五个点的位置，以右下点为（X0，Y0）
g.drawLine((int)x0, (int)y0, (int)x2, (int)y2);
g.drawLine((int)x2, (int)y2, (int)x3, (int)y3);
 g.drawLine((int)x3, (int)y3, (int)x4, (int)y4);
g.drawLine((int)x4, (int)y4, (int)x0, (int)y0);
g.drawLine((int)x2, (int)y2, (int)x5, (int)y5);
g.drawLine((int)x5, (int)y5, (int)x3, (int)y3);

//划线——注意方法所需要的数据类型
 Show(x2,y2,l*Math.cos(Math.PI/6),a+Math.PI/6,b+Math.PI/6,c+Math.PI/6,count-1,g);
Show(x5,y5,l*Math.sin(Math.PI/6),a-Math.PI/3,b-Math.PI/3,c-Math.PI/3,count-1,g);

//进行递归调用（注意传到方法里的点是相对于新正方形的右下点）
 }