其实,刚开始学迭代和递归的时候,完全没想过用它来画图···只是知道可以用递归计算,比如1+2+3+4+5+...+100=?然后,发现可以通过不断画线画点形成各种有趣的图形。
1.开始画的是利用一个点,通过迭代画出一层一层的圆,三角形,正方形,线。例如圆,先 要随机得到初始点的两个坐标;然后让坐标进行若干次的加(减),并改变宽和高,就能画出一层层的圆。
class="java">// 取随机数
Random random=new Random();
//得到随机数
x1=random.nextInt(500)+10;
y1=random.nextInt(500)+10;
x2=x1;
y2=y1;
a=x2;
b=x2;
//画矩形
if(command.equals("rect")){
//迭代次数
for(int i=0;i<20;i++){
//左移5
x1=x1-5;
//上移5
y1=y1-5;
//宽加10
x2=x2+5;
//高加10
y2=y2+5;
//设置渐变色,因为变化太小,所以*10
Color c=new Color(3+10*i,20+5*i,190+i);
g.setColor(c);
g.drawRect(x1, y1,Math.abs(x2-x1), Math.abs(y1-y2));
}
}
//画圆
else if(command.equals("oval")){
//迭代次数
for(int i=0;i<40;i++){
//每次画圆左移5
x1=x1-5;
//每次画圆上移5
y1=y1-5;
//宽增10
x2=x2+5;
//高增10
y2=y2+5;
g.drawOval(x1, y1,Math.abs(x2-x1), Math.abs(y1-y2));}
}
//画线
else if(command.equals("line")){
//迭代次数
for(int i=0;i<40;i++){
//每次画线起点左移3
x1=x1-3;
//每次画线终点右移3
x2=x2+3;
//起点上移3
y1=y1+3;
//终点上移3
y2=y2+3;
g.drawLine(x1, y1, x2, y2);}
}
//三角形
else if(command.equals("triangle")){
//迭代次数
for(int i=0;i<40;i++){
//x1,y1是中间的点,剩下的是底边两点
//顶点每次往上移动7
y1=y1-7;
//底边的点每次向上移动5
y2=y2+5;
//底边右点每次右移7
a=a+7;
//底边左点每次左移7
b=b-7;
g.drawLine(x1, y1, b, y2);//左线
g.drawLine(x1, y1, a, y2);//右线
g.drawLine(a, y2, b, y2); //底边
}
}
2.画完这些,就画利用迭代,通过函数构成的图形
Xn+1=d sin(a Xn)-sin(b Yn)
Yn+1=c cos(a Xn)+cos(b Yn)
当a=1.40,b=1.56,c=1.40,d=-6.56
开始画的时候,直接用的函数,自然是什么都显示不出来,因为画图时要用int,但是式中数值为double,所以要转型,如果直接转型,比如,1.49就变成1,0.50也是1,但这两个数值差很大,所以要将它们扩大若干倍,才能减小误差。//手镯
else if(command.equals("bangle")){
//按照滑动条的大小控制每次点击是增加的点
value=sl.getValue();
//取随机数控制颜色
Random r=new Random();
int c=2;
int c3=56;
int c4=r.nextInt(200);
for(int i=0;i<value;i++){
//改变颜色
c=0;
c3=c3+1;
//int c2=r.nextInt(255);
//int c3=r.nextInt(139);
double a2=(-6.56)*Math.sin(1.40*a1)-Math.sin(1.56*b1);
double b2=1.40*Math.cos(1.40*a1)+Math.cos(1.56*b1);
//第二种图形
//double a2=Math.sin((-2)*b1)-Math.cos((-2)*a1);
// double b2=Math.sin((-1.2)*a1)-Math.cos(2*b1);
a1=a2;
b1=b2;
c2=value;
//if(c2>200)
//c2=value/15;
g.setColor(new Color(c,c3,c4));
g.drawLine((int)(a1*20+400), (int)(b1*20+400),(int)(a1*20+400), (int)(b1*20+400));
//g.setColor(new Color(c3,25,25));
//第二种图形
//g.drawLine((int)(a1*40+400), (int)(b1*40+400),(int)(a1*40+400), (int)(b1*40+400));
}
}
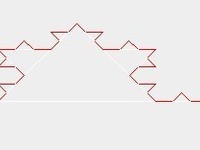
3.又高端一点的图形--科赫曲线
最初看到科赫曲线,就是好熟悉的感脚,不知从何入手····经过老师的引导,慢慢也画出来一个不会旋转的科赫曲线。思路就是,科赫曲线中一共有六种线,分情况讨论。/**
* 画科赫曲线
* @author zll
*
*/
public class Draw {
private Graphics g;
public Draw(Graphics g){
this.g=g;
}
/**
* 画科赫曲线
* @param x1
* @param y1
* @param x2
* @param y2
* @param n
*/
public void showDraw(int x1,int y1,int x2,int y2,int n){
int xx1,xx2,xx3,yy1,yy2,yy3;
if(n<1)
return;
//一三线隐藏
//横线上方
if((y1==y2)&&(x2>x1)){
xx1=x1+(x2-x1)/3;
yy1=y1;
xx2=(x1+x2)/2;
yy2=y1 -(x2-x1)/3*(int) Math.sqrt(3)/2;
xx3=x2-(x2-x1)/3;
yy3=y1;
}
//右上方斜线
else if((y2<y1)&&(x2>x1)){
xx1=x1+(x2-x1)/3;
yy1=y1-(y1-y2)/3;
xx2=x1;
yy2=y2+(y1-y2)/3;
xx3=x2-(x2-x1)/3;
yy3=y2+(y1-y2)/3;
}
//左上方斜线
else if((y2<y1)&&(x2<x1)){
xx1=x1-(x1-x2)/3;
yy1=y1-(y1-y2)/3;
xx2=x2;
yy2=yy1;
xx3=x2+(x1-x2)/3;
yy3=y2+(y1-y2)/3;
}
//直线下方
else if((y1==y2)&&(x2<x1)){
xx1=x1-(x1-x2)/3;
yy1=y1;
xx2=(x1+x2)/2;
yy2=y1+(x1-x2)/3*(int) Math.sqrt(3)/2;
xx3=x2+(x1-x2)/3;
yy3=y1;
}
//左下方斜线
else if((x2<x1)&&(y2>y1)){
xx1=x1-(x1-x2)/3;
yy1=y1+(y2-y1)/3;
xx2=x1;
yy2=y2-(y2-y1)/3;
xx3=x2+(x1-x2)/3;
yy3=yy2;
}
//右下方线
else{
xx1=x1+(x2-x1)/3;
yy1=y1+(y2-y1)/3;
xx2=x2;
yy2=yy1;
xx3=x2-(x2-x1)/3;
yy3=y2-(y2-y1)/3;
}
// g.setColor(Color.white);
// g.drawLine(x1, y1, xx1, yy1);
// g.drawLine(xx3, yy3, x2, y2);
g.setColor(Color.RED);
g.drawLine(x1, y1, x2, y2);
g.drawLine(xx1, yy1, xx2, yy2);
g.drawLine(xx3, yy3, xx2, yy2);
g.setColor(Color.white);
g.drawLine(xx3, yy3, xx1, yy1);
showDraw(x1,y1,xx1,yy1,n-1);
showDraw(xx1,yy1,xx2,yy2,n-1);
showDraw(xx2,yy2,xx3,yy3,n-1);
showDraw(xx3,yy3,x2,y2,n-1);
}
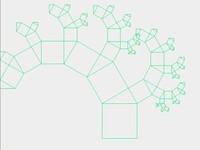
4.再高端一点点---毕达哥拉斯树 private double Q1=30;
/*
* 画树
*/
public void draw(int x1,int y1,int x2,int y2,int jiaodu,int n){
//设置退出
if(n>5){
return;
}
//起始线长
double s1=Math.sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));
//起始线角度
double sin1=Math.sin(jiaodu*pi/180);
double cos1=Math.cos(jiaodu*pi/180);
//三角形角度
double b=s1*Math.cos(Q1*pi/180);
//得到正方形左上方的点
double x3=x1-s1*sin1;
double y3=y1-s1*cos1;
//得到正方形右上方的点
double x4=x2-s1*sin1;
double y4=y2-s1*cos1;
//偏过角度的累加
double sin=Math.sin((jiaodu+Q1)*pi/180);
double cos=Math.cos((jiaodu+Q1)*pi/180);
//得到三角形的顶点
double x5=x3+b*cos;
double y5=y3-b*sin;
//画线
g.drawLine(x1, y1, x2, y2);
g.drawLine(x1, y1, (int)x3, (int)y3);
g.drawLine(x2, y2, (int)x4, (int)y4);
g.drawLine((int)x3, (int)y3, (int)x4, (int)y4);
g.drawLine((int)x3, (int)y3, (int)x5, (int)y5);
g.drawLine((int)x4, (int)y4, (int)x5, (int)y5);
//递归(三角型的两边)
draw((int)x3,(int)y3,(int)x5,(int)y5,(int)(jiaodu+Q1),n+1);
draw((int)x5,(int)y5,(int)x4,(int)y4,(int)(jiaodu-Q2),n+1);
}
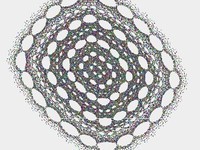
5.随意一点---网状图
改变函数的值,画出不同的图形,通过鼠标点击,慢慢画if(command.equals("net")){
for(int i=0;i<40000;i++){
double a=1.6,b=4.6,c=6.0;
Random r=new Random();
int c2=r.nextInt(200);
int c3=r.nextInt(200);
int c4=r.nextInt(200);
double a2=b1-Math.signum(a1)*Math.sqrt(Math.abs(b*a1-c));
double b2=a-a1;
a1=a2;
b1=b2;
g.setColor(new Color(c2,c3,c4));
g.drawLine((int)(a1*2+400), (int)(b1*2+400),(int)(a1*2+400), (int)(b1*2+400));
}
}
- 大小: 67.8 KB

- 大小: 20.3 KB
- 大小: 33.5 KB
- 大小: 8.1 KB

- 大小: 14.6 KB