Shallow and retained sizes_JAVA

您所在的位置：程序员俱乐部 > 编程开发 > JAVA > Shallow and retained sizes

Shallow and retained sizes

2013/9/24 13:05:34 明天属于我程序员俱乐部我要评论(0)

摘要：Referencefrom:http://www.yourkit.com/docs/java/help/sizes.jspYourKitJavaProfileriscapableofmeasuringshallowandretainedsizesofobjects.Shallowsizeofanobjectistheamountofmemoryallocatedtostoretheobjectitself,nottakingintoaccountthereferencedobjects
标签：all

Reference from : http://www.yourkit.com/docs/java/help/sizes.jsp

YourKit Java Profiler is capable of measuring shallow and retained sizes of objects.

Shallow size of an object is the amount of memory allocated to store the object itself, not taking into account the referenced objects. Shallow size of a regular (non-array) object depends on the number and types of its fields. Shallow size of an array depends on the array length and the type of its elements (objects, primitive types). Shallow size of a set of objects represents the sum of shallow sizes of all objects in the set.

Retained size of an object is its shallow size plus the shallow sizes of the objects that are accessible, directly or indirectly, only from this object. In other words, the retained size represents the amount of memory that will be freed by the garbage collector when this object is collected.

To better understand the notion of the retained size, let us look at the following examples:

In order to measure the retained sizes, all objects in memory are treated as nodes of a graph where its edges represent references from objects to objects. There are also special nodes - GC root objects, which will not be collected by Garbage Collector at the time of measuring (read more about GC roots).

The pictures below show the same set of objects, but with varying internal references.

Figure 1:?????????????????????????????????????????????????????? Figure 2: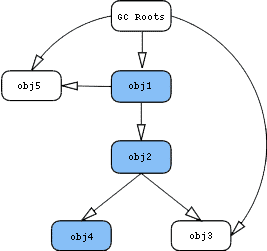
??
?

Let us consider obj1.
As you can see, in both pictures we have highlighted all of the objects that are directly or indirectly accessed only by obj1. If you look at Figure 1, you will see that obj3 is not highlighted, because it is also referenced by a GC root object. On Figure 2, however, it is already included into the retained set, unlike obj5, which is still referenced by GC root.

Thus, the retained size of obj1 will represent the following respective values:

For Figure 1: the sum of shallow sizes of obj1, obj2 and obj4
For Figure 2: the sum of shallow sizes of obj1, obj2, obj3 and obj4

Looking at obj2, however, we see that its retained size in the above cases will be:

For Figure 1: the sum of shallow sizes of obj2 and obj4
For Figure 2: the sum of shallow sizes of obj2, obj3 and obj4

In general, retained size is an integral measure, which helps to understand the structure (??lustering) of memory and the dependencies between object subgraphs, as well as find potential roots of those subgraphs.