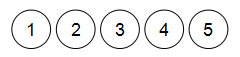哈弗曼树及哈弗曼编码简述_JAVA_编程开发_程序员俱乐部

哈弗曼树是一种特殊的hashu.html" target="_blank">二叉树。
　　定义：　　构造一棵二叉树，若该二叉树的带权路径长度为最小值，则此二叉树可称为哈弗曼树。
　　解释：　　带权路径长度：树中各叶结点到根结点需要经过的最短层数与该结点上权值的乘积之和。
　　构造方法：　　若有n个权值，则构建成功的哈弗曼树有n个叶结点。取n个结点中权值最小的两个合并，作为一棵新树的左右子树，新树根结点的权数为两子结点的权数之和。将新根结点权值与余下n-2个结点比较，得出权值最小的两个结点，再重复上述操作。
　　下面以权值分别为1、2、3、4、5的5个结点为例，来说明哈弗曼树的构造过程。
　　初始状态为五棵只有根结点的树组成的森林：　
   
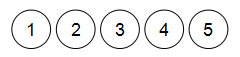
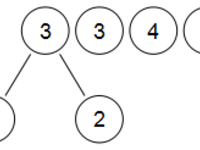
　　在五个结点中，1、2的权值最小，将1、2合并，作为新树的左右结点，新树根结点的权值为1、2之和：　　
   
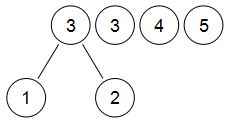
　　将新树的根结点与余下3个根结点比较，3、3的权值最小，合并得新根结点：　
   
　　在三个根结点中，4、5最小，合并成新树：　　
   
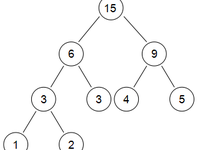
　　最后，在将6、9合并，得到一棵有5个叶结点的树：　　
   

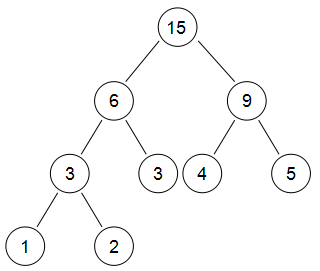　　用途：　　在计算机中，假设我们需要存储一段英文信息，那么出于节省存储空间、减少传输流量的考虑，我们一定是希望这段信息占用的空间越小越好。
　　如何达到这个目的呢？我们知道，一个英文字符占据一个字节大小，这是由计算机内部的编码解码规则决定的。在这种情况下，这段信息占据的大小就是固定的，不存在减少的可能。既然如此，为什么不自己定义一套编码解码的规则呢？根据一般规律，一段英文信息中一定有某些字母的使用频率较高，那么用最短的01串代表最常用的字母，字母使用频率越高代表它的01串就越短，这样就可以达到减少所需存储空间的目的。
　　至于如何获得代表各字母的01串，那就要靠哈弗曼编码了。上文中提到的方法，实际就是哈弗曼树中最短带权路径长度的概念。以每个字母的出现次数或频率作为权值，构造哈弗曼树，然后从根结点开始，左子树代表0，右子树代表1，依次往下推导，就可得出个字母的01串了。
　　以上图为例，代表5个权值的01串分别为：
　　1：000
　　2：001
　　3：01
　　4：10
　　5：11
　　
　　在掌握了基本的规则之后，我们也可以通过程序来实现哈弗曼编码的获得。
　　程序一共需要4个类：
　　
　　数据类：定义数据的属性及属性的setter、getter方法。属性应有：数据内容（如字母a或其他）、数据出现次数、数据的哈弗曼编码。

class="java" name="code">/**
 * 数据类，每个数据都应有数据内容，出现次数，和它的哈弗曼编码
 */
public class Data {
	private int number;
	private int time;
	private String code;
	
	public int getNumber() {
		return number;
	}
	public void setNumber(int number) {
		this.number = number;
	}
	public int getTime() {
		return time;
	}
	public void setTime(int time) {
		this.time = time;
	}
	public String getCode() {
		return code;
	}
	public void setCode(String code) {
		this.code = code;
	}
	
	
}

　　结点类：定义结点的属性及属性的setter、getter方法。属性应有：结点代表的数据，该结点的左右子结点。

/**
 * 结点类，每个结点都应有左右子树、结点代表的数据
 */
public class Node {
	private Data data;
	private Node leftChild;
	private Node rightChild;
	
	public Data getData() {
		return data;
	}
	public void setData(Data data) {
		this.data = data;
	}
	public Node getLeftChild() {
		return leftChild;
	}
	public void setLeftChild(Node leftChild) {
		this.leftChild = leftChild;
	}
	public Node getRightChild() {
		return rightChild;
	}
	public void setRightChild(Node rightChild) {
		this.rightChild = rightChild;
	}
	
}

哈弗曼树类：定义创建哈弗曼树的方法和将哈弗曼编码显示出来的方法。

/**
 * 传入数据数组，获取各数据的哈弗曼编码 */
public class HfmTree {
	public Data[] data;

	public HfmTree(Data[] data) {
		this.data = data;
	}

	/**
	 * 将数据数组转换为结点数组
	 * @param 要转换的数据数组
	 * @return 转换得到的结点数组
	 */
	public Node[] arrToNode(Data[] data) {
		Node[] nodes = new Node[data.length];
		for (int i = 0; i < data.length; i++) {
			Node node = new Node();
			nodes[i] = node;
			nodes[i].setData(data[i]);
		}
		return nodes;
	}

	/**
	 * 将结点数组按数据出现的次数进行从小到大的排列（冒泡排序）
	 * @param 要进行排列的结点数组
	 */
	public void sortNode(Node[] nodes) {
		for (int i = 0; i < nodes.length; i++) {
			for (int j = i + 1; j < nodes.length; j++) {
				if (nodes[i].getData().getTime() > nodes[j].getData().getTime()) {
					Node temp = nodes[i];
					nodes[i] = nodes[j];
					nodes[j] = temp;
				}
			}
		}
	}

	/**
	 * 建立哈弗曼树方法
	 * @return	只有一个最终根结点的数组
	 */
	public Node[] creatHfmTree() {
		//定义存储根结点的数组，并用由数据数组转换而来的结点数组初始化
　　Node[] nodes = this.arrToNode(data);
　　//循环进行排序，合并结点，获得新根结点，获得新根结点数组操作
		while (nodes.length > 1) {
			this.sortNode(nodes);
			Node n1 = nodes[0];
			Node n2 = nodes[1];
			Node n3 = new Node();
			Data data = new Data();
			data.setTime(n1.getData().getTime() + n2.getData().getTime());
			n3.setData(data);
			n3.setLeftChild(n1);
			n3.setRightChild(n2);

			Node[] nodes2 = new Node[nodes.length - 1];
			nodes2[0] = n3;
			for (int i = 2; i < nodes.length; i++) {
				nodes2[i - 1] = nodes[i];
			}
			nodes = nodes2;
		}
		return nodes;
	}
	
	/**
	 * 应用递归打印各数据的哈弗曼编码
	 * @param node	第一次传入根结点
	 * @param code	第一次传入""
	 */
	public void printCode(Node node,String code){
		if(node.getLeftChild()!=null){
			this.printCode(node.getLeftChild(), code+"0");
		}
		if(node.getRightChild()!=null){
			this.printCode(node.getRightChild(),code+"1");
		}
		if(node.getLeftChild()==null&&node.getRightChild()==null){
			System.out.println("数"+node.getData().getNumber()+"次数为" +
					node.getData().getTime()+"编号为"+code);
		}
	}
}

测试类：测试程序的正确性。随机建立一个数据数组并获得各数据的哈弗曼编码。

import java.util.Random;

public class Test {
	
	public static void main(String args[]){
		Data[] datas = new Data[10];
		Random r = new Random();
		int ran;
		for(int i =0;i<10;i++){
			Data data = new Data();
			ran = r.nextInt(50);
			data.setNumber(ran);
			ran = r.nextInt(20);
			data.setTime(ran);
			datas[i] = data;
		}
		HfmTree ht = new HfmTree(datas);
		Node[] nodes =ht.creatHfmTree();
		String code = "";
		ht.printCode(nodes[0], code);
	}
}

　　程序运行结果如下：

   

　　可以自行验证程序结果的正确性。
　　使用随机数的问题：有可能得到相同的数据内容。对此，多运行几次即可得到满意的实验数据。

• 
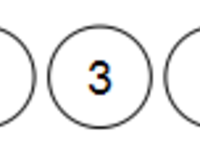
• 大小: 5.3 KB

• 
• 大小: 7.6 KB

• 
• 大小: 10 KB

• 
• 大小: 12.3 KB

• 
• 大小: 15.1 KB

• 
• 大小: 6.2 KB

• 查看图片附件