数据结构——并查集_C/C++_编程开发_程序员俱乐部

     让我们首先了解一下什么是并查集。并查集的英文：Disjoint Set，即“不相交集合“，将编号分别为1…N的N个对象划分为不相交集合，在每个集合中，选择其中某个元素代表所在集合。
    常见两种操作：
        合并两个集合
        查找某元素属于哪个集合
　　这也就是这种数据结构叫并查集的原因！！！，下面是一种最简单的实现方法。



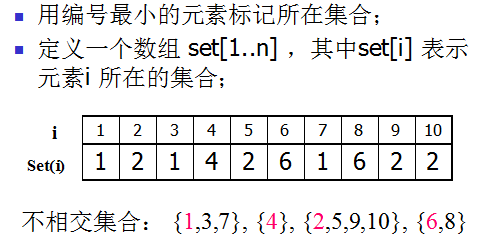
　　这种方法合并的时间复杂度是O(n)，查找是O(1)的复杂度。伪码如下：
　　
　　


　　
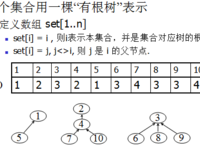
　　有没有优化的方法呢？当然是有的，因为上面我们合并两个集合必须搜索整个集合。那如果我们采用树结构呢？这的确是个好想法。
　　


　　大致伪码如下：
　　


　　还可以优化，路径压缩。
　　思想：每次查找的时候，如果路径较长，则修改信息，以便下次查找的时候速度更快
　　步骤:
　　第一步，找到根结点
　　第二步，修改查找路径上的所有节点，将它们都指向根结点
    伪码如下图：
　　


　　废话不多说，让我们通过实例来理解。
　　畅通工程(HDOJ-1232)
　　题目描述：某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？
　　分析：若每个城市之间有且仅有一条道路相连，那这肯定是一棵树了。边数 = 节点数 -1 ，只要我们知道城市被分成的集合数ans，要修的道路就是ans-1 ，下面贴出经过路径压缩的并查集。

　　

class="c++" name="code">
#include<iostream>
using namespace std;
int set[1005];
//带路径压缩的并查集查找 
int find(int a){
    int root = a;
    while(root!=set[root]){
        root = set[root];                       
    }
    //路径压缩 
    int i=a;
    while(i!=root){
        int j  =set[i];
        set[i] = root;
        i = j;    
    }
    return root;
}
int main(){
    int n,m,a,b;
    scanf("%d",&n);
    while(n!=0){
        scanf("%d",&m);
        for (int i=1;i<=n;i++)
           set[i] = i;
        for(int i=0;i<m;i++){
           scanf("%d%d",&a,&b);
           int aRoot=find(a);
           int bRoot=find(b);
           if(aRoot!=bRoot){
              if(aRoot<bRoot){
                 set[bRoot]=aRoot;                
              }else{
                 set[aRoot]=bRoot;      
              }  
           }       
        }
        int sum=0;
        for (int i=1;i<=n;i++){
            if(i==set[i])
               sum++;   
        }
        printf("%d\n",sum-1);
        scanf("%d",&n);            
    }
    return 0;    
} 

• 
• 大小: 13.3 KB

• 
• 大小: 8.1 KB

• 
• 大小: 14.6 KB

• 
• 大小: 9.7 KB

• 
• 大小: 6.6 KB

• 查看图片附件