【高次幂取模的应用】HDU 3609 Up-up_C/C++_编程开发_程序员俱乐部

题目很容易看懂：http://acm.hdu.edu.cn/showproblem.php?pid=3609

降幂公式：

这速度可以排到前10了：

#include <iostream>
using namespace std;
#define LL unsigned __int64
#define M 205

int phi[M];

int Euler (int n)    //求n的欧拉值
{
	int i, res = n;
	for (i = 2; i * i <= n; i++)
	{
		if (n % i == 0)
		{
			res = res - res/i;
			while (n % i == 0)
				n /= i;
		}
	}
	if (n > 1)
		res = res - res/n;
	return res;
}

LL qmod (LL a, LL b, int c)    //快速幂取模
{
	LL res = 1;
	for ( ; b; b >>= 1)
	{
		if (b & 1)
			res = res * a % c;
		a = a * a % c;
	}
	return res;
}

LL isok (LL a, LL b, int c)    //目的是判断a^b是否>=c
{
	LL res = 1, i;
	for (i = 0; i < b; i++)
	{
		res *= a;
		if (res >= c)
			return res;
	}
	return res;
}

LL upup (LL a, int k, int num)    //按照题意递归地使用公式
{
	if (phi[num] == 1) return 1;    //显然符合公式条件，很容易套公式知道是1，这实际上是剪枝
	if (k == 1) return a % phi[num];//返回上一层的a的幂
	LL b = upup (a, k-1, num+1);    //得到a的幂b
	LL x = isok (a, b, phi[num]);
	if (x >= phi[num])    //使用公式的条件，满足条件可以进行降幂，返回的是上层a的幂
		return qmod (a % phi[num], b, phi[num]) + phi[num];
	else return x;    //不使用公式，直接返回a^b，也属于上层a的幂
}

int main()
{
	LL a;
	int k;
	phi[0] = 100000000;
	for (k = 1; k < M; k++)
		phi[k] = Euler (phi[k-1]);    //预处理所需欧拉值
	while (~scanf ("%I64u%d", &a, &k))
	{
		printf ("%I64u\n", upup (a, k, 0) % phi[0]);
	}
    return 0;
}

• 
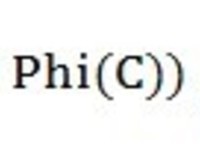
• 大小: 8.2 KB

• 
• 大小: 12.1 KB

• 查看图片附件