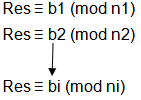模线性方程组-中国剩余定理（非互质版详解）_C/C++_编程开发_程序员俱乐部

该专题必备知识：解模线性方程
http://972169909-qq-com.iteye.com/blog/1104538

【需要的话可以到代码下面下载中国剩余定理非互质详解文档版】
以下原创
转载请指明作者 (KIDx) 以及 文章地址：
http://972169909-qq-com.iteye.com/blog/1266328


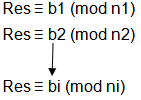问题描述：给出bi，ni的值，且n1, n2, n3,…, ni两两之间不一定互质，求Res的值？
解：采用的是合并方程的做法。
这里将以合并第一第二个方程为例进行说明
由上图前2个方程得(设k1、k2为某一整数)：



【需要的话请到代码下面下载中国剩余定理非互质详解文档版】
例题： hdu 1573 X问题 【下面已给出代码】
http://acm.hdu.edu.cn/showproblem.php?pid=1573
另外推荐一题： hdu 3579 Hello Kiki：
http://acm.hdu.edu.cn/showproblem.php?pid=3579

#include <iostream>
using namespace std;
#define LL __int64
#define M 10
int N;

LL Egcd (LL a, LL b, LL &x, LL &y)
{
	if (b == 0)
	{
		x = 1, y = 0;
		return a;
	}
	LL d, tp;
	d = Egcd (b, a%b, x, y);
	tp = x;
	x = y;
	y = tp - a/b*y;
	return d;
}

LL CRT2 (LL b[], LL n[], int num)
{
	int i;
	bool flag = false;
	LL n1 = n[0], n2, b1 = b[0], b2, bb, d, t, k, x, y;
	for (i = 1; i < num; i++)
	{
		n2 = n[i], b2 = b[i];
		bb = b2 - b1;
		d = Egcd (n1, n2, x, y);
		if (bb % d)		//模线性解k1时发现无解
		{
			flag = true;
			break;
		}
		k = bb / d * x;    //相当于求上面所说的k1【模线性方程】
		t = n2 / d;
		if (t < 0) t = -t;
		k = (k % t + t) % t;	//相当于求上面的K`
		b1 = b1 + n1*k;
		n1 = n1 / d * n2;
	}
	if (flag)
		return 0;			//无解
/******************求正整数解******************/
	if (b1 == 0)	//如果解为0，而题目要正整数解，显然不行
		b1 = n1;	//n1刚好为所有ni的最小公倍数，就是解了
/******************求正整数解******************/
	if (b1 > N)
		return 0;
	return (N-b1)/n1+1;    //形成的解：b1, b1+n1, b1+2n1,..., b1+xni...
}

int main()
{
	int t, num, i, cc = 1;
	LL b[M], n[M];
	scanf ("%d", &t);
	while (t--)
	{
		scanf ("%d%d", &N, &num);
		for (i = 0; i < num; i++)
			scanf ("%I64d", n+i);
		for (i = 0; i < num; i++)
			scanf ("%I64d", b+i);
		printf ("%I64d\n", CRT2 (b, n, num));
	}
	return 0;
}

• 
• 大小: 1.9 KB

• 
• 大小: 18.1 KB

• 
• 大小: 20.3 KB

• 中国剩余定理非互质详解.zip (13.7 KB)
• 下载次数: 6

• 查看图片附件