Codeforces Beta Round #1_C/C++_编程开发_程序员俱乐部

int main()
{
	LL n, m, a, res;
	while (~scanf ("%I64d%I64d%I64d", &n, &m, &a))
	{
		res = ((n+a-1) / a) * ((m+a-1) / a);
		printf ("%I64d\n", res);
	}
	return 0;
}

int main()
{
	char s[105];
	int t, i, len, key, r, c, k;
	scanf ("%d", &t);
	while (t--)
	{
		scanf ("%s", s);
		len = strlen (s);
		key = 0;
		for (i = 1; i < len; i++)
			if (isalpha (s[i-1]) && !isalpha (s[i]))
				key++;
		if (key == 1)    //输入的是第二种表示，如BC23
		{
			c = 0;    //求是第几列
			for (i = 0; i < len; i++)
			{
				if (!isalpha (s[i]))
					break;
				c *= 26;
				c += s[i] - 'A' + 1;
			}
			r = 0;    //求是第几行
			for (; i < len; i++)
				r *= 10, r += s[i] - '0';
			printf ("R%dC%d\n", r, c);
		}
		else    //输入的是第一种表示，如R23C55
		{
			r = 0;   //求是第几行
			for (i = 1; i < len; i++)
			{
				if (s[i] == 'C')
					break;
				r *= 10;
				r += s[i] - '0';
			}
			i++;
			c = 0;    //求是第几列
			for (; i < len; i++)
				c *= 10, c += s[i] - '0';
			k = 0;
			while (c)    //将列转换成字母表示形式
			{    //跟普通的进制转换有区别！
				c--;    //突破口！琢磨很久才出来的一个想法！
				s[k++] = c % 26 + 'A';
				c /= 26;
			}
			for (i = k-1; i >= 0; i--)
				printf ("%c", s[i]);
			printf ("%d\n", r);
		}
	}
	return 0;
}

C题
参考白衣少年：http://hi.baidu.com/%B0%D7%D2%C2%C9%D9%C4%EA2012/blog/item/abb86a05be0953037bec2cfe.html
题意：有一个正n边形
输入正n边形的其中3个点
问正n边形可能存在的最小面积，已知n<=100
该题关键技巧就是要画外接圆，然后玩玩圆周角，圆心角这些概念，当个平面几何问题，先尽量多推出一些结论。
具体解法如下:
首先，随便画个正多少边形，画个外接圆。根据正弦定理，可以直接知道外接圆半径。把这三个点连成一个三角形，三个角都会是正x边形的一个边对应这个外接圆的圆周角的整数倍。由于x很小，枚举+判断就可以了。
三角形外接圆半径公式：

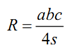
每条边所对应的圆心角 = 2*PI/n
所以圆周角 = 圆心角/2 = PI/n
正n边形面积：

const double EP = 1e-3;
const double PI = 3.1415926535897932384626433832795;

struct point{
	double x, y;
}p[5];

double dist (point a, point b)
{
	return sqrt ((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
}

double area2 (point a, point b, point c)
{
	return fabs(a.x*b.y+b.x*c.y+c.x*a.y-c.x*b.y-b.x*a.y-a.x*c.y);
}

bool isok (int n, double ang)   //判断三角形的角ang是不是边对应圆周角PI/n的整数倍
{
	double tp = n*ang/PI;   //思路：判断相除的结果是不是整数
	double x = floor(tp+EP);
	if (tp - x < EP)
		return true;
	return false;
}

int main()
{
	int i, n;
	double r, a, b, c, s, A, B, C, Rang;
	while (~scanf ("%lf%lf", &p[0].x, &p[0].y))
	{
		for (i = 1; i < 3; i++)
			scanf ("%lf%lf", &p[i].x, &p[i].y);
		a = dist (p[0], p[1]);
		b = dist (p[0], p[2]);
		c = dist (p[1], p[2]);
		A = acos ((b*b + c*c - a*a) / 2 / b / c);
		B = acos ((a*a + c*c - b*b) / 2 / a / c);
		C = acos ((b*b + a*a - c*c) / 2 / b / a);
		s = area2 (p[0], p[1], p[2]);    //求三角形的面积的2倍
		/*double p = (a+b+c)/2;
		s = sqrt (p*(p-a)*(p-b)*(p-c));*/
		r = a*b*c/2/s;    //由于s已经是三角形面积的2倍了，所以除以2即可
		for (n = 3; n <= 100; n++)   //枚举边数，边越小面积越小
			if (isok (n, A) && isok (n, B) && isok (n, C))
				break;
		Rang = PI/n;    //中心角的一半
		double res = n*r*r*sin(Rang)*cos(Rang);
		printf ("%.8f\n", res);
	}
	return 0;
}

• 
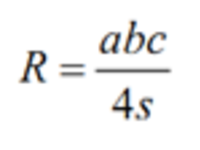
• 大小: 1.7 KB

• 
• 大小: 6.8 KB

• 查看图片附件