先看效果看

加载了一张image,根据四个顶点任意变换。
知识点:1.BitmapContext 2.矩阵变换
一.什么是BitmapContext
官方解释:
The number of components for each pixel in a bitmap graphics context is specified by a color space, defined by a CGColorSpaceRef. The bitmap graphics context specifies whether the bitmap should contain an alpha channel, and how the bitmap is generated.
通俗来讲:
首先,我们根据图片创建一个BitmapContext,把一张图片绘制到这个BitmapContext上。这时你可以把图片看成是由很多个彩色的点组成的。

图片局部放大后就形成了一个表格。每个单元代表一个像素点其中包含了4个元素:alpha(透明度)红 绿 蓝

QQ9alPxwX1jU9ndBify4gz+sbRGWUcF8YFFxxH0RHXARSeFkWWInsLIpStlLbQJemSPU3u++O2CWmTNghIqufzD/Tem5tzv+d3vvd3lnsjybIsIxAIBN0Y1akugEAgEBwvwsgEAkG3Jy3RjtVFy3j31afIMBlOdRkFAoEAV0DmwScXYrfbO+xLaGQ7Nq3lEsNuCiyaU11+gUAg4JOKEHv37j02I5NUEhoV2I3qU11+gUAgQK0KJdwnxsgEAkG3RxiZQCDo9ggjEwgE3R5hZAKBoNsjjEwgEHR7hJEJBIJujzAygUDQ7RFGJhAIuj3CyAQCQbdHGJlAIOj2CCMTCATdnrTjP8XJYU9tgCCQk6nGnnZin/fcUxtA0sGADG3Sn2loDrHXFWRgthZL2snz/7brbo+kAqteRa7p1FVZVV0LdeEQQ7O1aCSpa82aQnxa5uaAO4guTSLLouas3gZOsySv+w+BakcLDaFwzDYNEAxBpkVFrqHzOm1oDnGwqYVMm4o+hsQvcXC7whz0ttAzM+2kxmgqkpJGVnmghXGvHwDg8ulmFozLO2Hnlv1w82vVlBn87PzvgVhUyVX49h1+Ziw/xAPX2fltf3tSn/muZSv1+hMeY8qTWHBZT6blmE5KGTrj1SUN/LXcQdncAdilzm8ub61s4o5Vh+PuGzNaz9sX98Ku+nG8kOCVjxXdEnH7xZn8cWx2wv1tsTfnahu/G5yV8Lgt230nPUZTlZQ0siVbXJH/f7rVRf3Y0IkLehVkp6k5YO46ozgaTdqxHX88ZQOYcqaJPG20erw+mX+VNuGulrnm+UpW3d+P4VrdyS/TUVhMakx5Eml0rsWzHzj5fUktAIVnGLlpuAVNi8RX33p4qaSBTZt9XBw8yFc/z08qs+vuWExKnV46xkw/nYZA69vl9xwK8FmFm78vdRLQyPzlzJy4n2+LPV0XMfi9xGiKknJGJnvhrbLGyN/uapmVDg+zssynumgASK0NTw6DtyWMRiOdlMZ473Q7o3T6mG3P/LQHl714iGK3l5VVHobnf79Glgy7vg1ETOwP12Tzq0GZkX0XD03nzrE2Rry6j92lQT4a72JWj9So1++DX/00s0OdLv6siVvXHGZbnb/Lz+taew/BkEwLYFD/eI2rPSlnZFt3+yj1+pk4wcgVUgZ3rDrMWzsamTUxNuDlIDxV5KCsJcBdk20M0SvjLks2uHhyQz0ltUpgFPRM46pxFu4+wxbXcHbs9HPvhhrOO92Ia3+Y53Y4ARg1TM8T03IYbY4NPE9jmHlL63l0Yz0Aehu8elWvmK6esz7En1fV81JJQ2Tb1DEmbj83kwk2Y1I6uINhaOdTWrPEpQPMFJd4sevUcXUYrNZy3+IaDmYGuXOQjfvfq2GfNcD22QOwqFTUHA4x99Na3i1vAmDkID2/PNfKFfkZMd+1ptTDA5/UUur1o7fBvRdk4QqHOy2zHIb5/6foN3OqOcbE2ujVJ42Hh2Xz+29q2dXoh1Yj27Hbz3M7nfTvr+GeEUq3SPbCYyvqeHKrI6LhncNt/OPrRi6cYGJWnpkt2338pvgIN19gpWFXmIc21MZ0rRataeIvX9ZSHlTeZXX1eRncV2injyY61tSVJnIQ7nr3CJp8iatyM/jD8lrW1XgBmHZuOs9Pzk1qiCJenU4aZoI1YDwqNtvXaRvryrzsWRvgjdYb/chBeh67KJuzrfHf4rxlu4+7Vx3hlhlWru1tidk+e10VT8/KpTAzGo/JaJWqpJyRvb+pGYBLTzMzLWyCVVBc4qGiMEgf9VGChuGjbc2Uev1cOzGDIWj59EsX139RBcD4wUbCHpl1h7w8/mE9h0ItPDO6R4fvc7nDrN3vZe1+JTCnnG6iel8LW77xceE3B/n8t30ZZYqa2VMfKY2qoGca4VqZckeIa56v5JM5fTg73UDYDZe9cihiAD/NMVOy18PyTW6Wb3Kz7cGC2OtIgFbV0XTlMGyqUMrpagnH1WGwWktppZ/i3V6Wr3cDYLIq59q/N8iYf+5XtuVJnKHWs67My21lhymd5eeR05VxmqJ1bmatqAQUo/Y54OH36gAw9+skCwjCHn8AgFuGWxMeducVmdwcsGDURhu/0xHina1NjDUYuGeEnbAbLnm+gmK3cr1nZOsiGgIMHKtoGPDJbKv086t/HomcS6dSIYfhoTdrmb/PGYmHNbs9LFrVxAfbm1h/u1IPyWpSeThIUZmHV2kA4MxeOrZV+vl0rYsb1FV8MKn3MddpwC/z1OdKPMW8wLRdnWpau/KfrlWGXEbm63BWtrC1zMf0pyv4eE5vCtM73iADPpmSWj/VgZYO2/dXtfBlrYfCTGPSWqUyKWVkrtow8yuc6G0wuYeRzLCaSWYjRQ4Pn1S5ubWPNXqwBi4900yBT4tVrQRB0XYPAM/dmss1ecrddPfuAOcsOkBFQ7DL73/p1jxm5ZmR/XDbi9UsdjbzyPq6DkE67/oe3FhgQQ7CfYtqWLC/ga+qPZw9yED1kSClXj/24SpKZg7AIEnIYbj3tRpePtRAuTdIn/Sug2LdPi+N+mgGFPDJvLO2iSVOF3obXNjTlFAHY2uDMeVJLJzRk7E2AxkhFTd/pJj83ZfamDtSGTRevcnDjCWHeG6xkxtOs5Lv0TBnpTJIf/8Vdu4ZZkcOwmMf1/HkdgfhQOIyNzhDFLu9mPtJnGaMph4Bv0xJnK6TzigxIlM5Lic7jStHZNC/h6LN+6ubIudafW0+fTQatu7yMentgwm//5oLM3hwdBZ2vZqtW3zM3+fE3E9iyeV9GWHWEXDJ3PxyNUsdLp7Y7uDpYT2456MjXWpSQLS+Bg3VsHhGb/roNWzZ7mPyewfZuMdL/fldj+P+8s1qMo6aJNlWGdXk0XFHDfa3q1M30Th467aeTMtNR/bDXW8f4Y0Djcz72kHhpOQy/Rj9W8fUtm7tWqtnzuxxzOf/PkkpI1v9jWJEF51lVu4Aapg9xkrRFx4Wb2+OMTJJBb+ZGk275TCMPkfP86Zcrmo1sWBIxhMKJ/Xd115kYVae0s2RdPD4rBwWL2iOBGkbY39i4MYCJU2XNPAfwzNYsL8BWuMzmAaPXpxN4RAjBkkiGJIJBqI/HaohuXGNtgwoHrdcZKN/6x2ygw5H+fXfZ+Ux2aYYnqMqRFGzB8tAKdJgAQrHGJmz08a8vQ6Ka7zUVbdQHgwxdpyBe4bZI9d537Qs3t3ViEPbtZ7tzc5VH2bKyx0NaOg5WtZMzQdg8AAtLwzIjVzD2zuUbt5rM3tGujYjh+h56Zxcbi3uOBs6Z
JSG58bnRv7+fKeSuT08JYcRZsUstekST1/Zg6ULXCz9ton7s+1JaVKQFTWyZy7KpY++tTzD9ExaYWSD1tvlBAjA/qoWoCXuvue2OfnfUdlx63Q9SlY6+3Ir03LTlWN08Oi0bN54obFDjB4ryWj15zNyMKTwxEzKGJkchDe3KMG7vMTF3Y4j+GSZ8p1Ky9z4tZftk/0JZ+okFVw1KoMPNjVz5RuVlFX4In39ZBicHbu2KTNbyQbbB+mUgbF3vkA49veN8/tquFRj5pnPHBRXeyNjdcfKxAlGrrJlRGa4Aj6Z99c0U+z2smCZg9m3WzpN9/U2ON0S1aqsSnGXxj0yYxbsQ241mwxJHSljlTfIgLByzvMKYsddVCa4JDeDhYGGY74WXbrE3AuylGhTweHdLSzY30COJnH4ecIy5n4SY9JjyzEgO/4atAn9omOUsh+KqpWb4m8WHOH1Xg00+kNYdOpIFhRohO2H/Elp0kb7TJNj9I6P7+5NYYaRYEip02BQ5vNtHn7xaRXzP3ZS2M/IVFviZTXT+sbuM6YrXXOVlqSMNB7JauWRwxik1F0ukzJGVlURZGmjMgbgrpZ5vbqxwzEf7mtm+GnxjUwOwvXzqyLnKOiZxqV5ZvqqNTz7deI1PG1UuLrueibDlm0+Jn8YzT7GDzYytqee9Ru8kfGeZHhofFaHGa6bhlsZ8+xeyh2hLruoGrMUs9Yr2GqIehvk6TQxg85TckyEvWBXR8PBou0YtBadKlFCAYA1U805JgPF1V42ubxMylAanilDxd3nRTMMf4HMghcaOr1+o+rYGmafBL/2NTJfh1FSYWodjxs/2Ihdq8avC0c6bMlqcrxoWq9Jo47++7Oz03mg3M6fdtZTWu/r1MiC7bSX0mCEQccBOunvx8Hpju/AnWn1XY3y+yJljGzJNiW9nTnVzLyRPfAElDDTaCTWbfTyi6IqXtvm5N4h9rizj7W1LSxtdGHuJ7H0ir4MNylRGXaSlJG1N4VAs0xRswdTukQLcpefb2NZqWKkd8+0MXdEtLvyoqOB4hIvwSTPFQjKHWa4JBOclW6k3NmcdBe1jUyDYkzDhxhYMqVPzL4D1UH2BAJM7GtkfbVitsWHvNzZPzrrKPvh35UuVDmdfIk
GemvTwA2vbG1k0nnxG+XCtY10SljJyJrLZerlEJajnqRzeuI3Qv/RM6pHlePBy7OYlH5UthaEz/a76dNDQ6hCTkqTzsz7ROBvHXrQaTqf+dxY540xOndTmFKvH1Og81jQtXsSsS0TPRatkl04fqpIidKF3dG1YzcMs2DRq8jLSCMvI40sg5oppyviOr+VWd+a1chhWLvXy7I9LupbQjiblEAe0lMfMTGABasbAOgqK/7LijoqQtGs7KUvlc+dNcSQ9GJcOQzlDuUcFxREu6A1VS28sFNZrmHSfHfJJRWMyIvN0trrkIiBvZUu2cZ1Xoqc7sh2tyPMz187yJULK9ns9tHLrhj6ym0utrh9keNWbnZT6vV3OtgvqeDXk5TM65OVLuZuqe1wzHtfNXN/SU2H7bX1IZbuclF8xIukg+GtkwBPbY7ehCorWpj1eWVSOv2kv6L/K5tjTXPR541ctaiS2RurktbkRNH+JiYHFT3m7VWucVyWvtM6feELJ/uOitHXVivXNnGEqVOj+feu6ALz/XuD/GlP/TFrleqkREa2bZeydizzNIkx5o5rYnQ2idm9rbx8qIF/7W6mcLQRgnD/ezWUev0sntOL8TlKZWxc5+WmcDXnWgx8sLU5st7niy88vJnfyDW5FjzhjlmRu1qm8I0DPDQ6m683+yJriu4YlUmySCoY08fAYmczV79VyZxRdpxHwjy7KdoYHy6q45WpeQnNsa1siTI3v6wY9lc1Hs5ON3TQ4QKNKe716awSj43O4f7NNcx6ppK7ptiwt6iZW6SYzcQJRuV8g4hoPfnJg/z6fBu+pjAvbm4AlPGYzjLU04freOAbpas0/2MnCzc0MHtIJnIAVm5xJ3z8aleZn+uWV3HaWRrWXlTAL8/P5OV/NvDmska+OeDnwkwTT6yJNsAMTec3lyvONjNn0xE+WeniwvqDXJ9vYdNOX2QN1uNn5aDLSE4T2U9cTdsyx65oq7MZ8w4lPGb6BemK/krlx9SpqTXfcFfLTHzlAA+MzWLrTj/v7lFidM5IW9xzDm4z6q+9zPAd4nyrkT+u6jiJlIxWqU5KZGSr9ypmc+OZmQlnRmacoczWLC1rwivLkcd59DbI12nR2SQWTe8FwIfrm/mfFTWsq/Hyp8uz+c9eyizj/B0OUBH3IXS9DZrLZe75oCZiYs/e0CMyzqPVtD4mkkCytu03XmjhYks67mqZR5bV8ewmBxNGG3n5Z8rzoqu+9rDNk/gub1RJ6G3QUxd/zMfc2kV8foMjrg6Jrg/gtp9ZeXycEpR/W+GINNhp56az8PyekeP+fE0O1+Urmj39hYMXNzcwYbSR6wYp27oaL/ntlXZen6acz10t8/QXDp5Z66DU62f0GXo23JvPAwPteOSjZnNblwIU9lL0LhigYfONBZxjMrDlGx9PrKln4KC0SBnaBtoT1Ut6torts/szwqBjc4mPuz4+whtljehtsPC2nhRmGJPXJJGmbd2yLuisyzhykJ4nr87hzfOi+neo01b+6yeZuKtlfvfvWt7d04TeBu/e0YtRBn1cLTJz1bzX2iZWl3j446o6LAMl7hlvjzkuWa1SGUmW5bi3lJfmzWXw7n9wZruuTKrT9gYASQX9bJrIOq6mQBhUYNHGBtX6jV6mL63g8ZtyuCXHyrfOAEGVzKBs7XFNN++pDeAJyVjNKvqaFFPy+MIEAaPu5DzWlCxtb1PQaCWy09VkGeIbX3ldkFp/CKtJxUDrsb+xQg7CHkeAxpYwkgp6WdO6fNNDG2VVAerCIUb20iP7ZYKtdXd0fcWsK0xUhrBSF15ZxqiX6GfRxNU+WU1ONR5vmHJXC0E5+RhtaA5xOBDCqJHIM6cljL1ktTpVLCoLMPbX7zBu3LgO+1Kia3kiMaWrGJoe2+gkFVj0nSefTcEQkg6G5p6YV8wMjLNMwKhPiQQYq1mN1dx1Q+2XpaEf331Ft6SBQT2+m57vrGjir+UOZk418/I5SjZ74ECQ6UsrABhpT+45U0mVXBmS1eRUYzSoGGo4Nk2tZjVWur62ZLVKRX5wRnasBFuSn5EUfH9cO8HCX8sdvL+8mWUbmhltMUQeI5s51cw4o+E4v0HwQ+JHb2S9czVcOSKDwcbUe5PEj5mCARo2zy7gb+sdrKp2U9UcZPxgIz8fmc5NQ62nuniCFONHb2T5+RpeyM89/hMJTjj5vTT8bWZqP+MnSA1SY9BGIBAIjgNhZAKBoNsjjEwgEHR7hJEJBIJujzAygUDQ7RFGJhAIuj3CyAQCQbdHGJlAIOj2CCMTCATdnoQr+0OhMBWNLTg8nlNdRoFAIGDroSBjE+xL+BofR309RSuWRX5ZWyAQCE4lBpOJ6ZdcFteTEhqZQCAQdBfEGJlAIOj2xIyRyXIIn9/Xwd1U6jQ0GvGaG0HyBIN+wqH2Pz8kkabRoj6BP7Em+KEj4/V5OniSpFKh1UbfSSe6lgKBoNvz/4RThPUuQiuuAAAAJXRFWHRkYXRlOmNyZWF0ZQAyMDE3LTA5LTE1VDE2OjQ3OjQ3KzA4OjAw16qkzAAAACV0RVh0ZGF0ZTptb2RpZnkAMjAxNy0wOS0xNVQxNjo0Nzo0NyswODowMKb3HHAAAABOdEVYdHNvZnR3YXJlAEltYWdlTWFnaWNrIDYuOS4xLTEwIFExNiB4ODZfNjQgMjAxNy0wOC0wMyBodHRwOi8vd3d3LmltYWdlbWFnaWNrLm9yZ2K/pMsAAAAYdEVYdFRodW1iOjpEb2N1bWVudDo6UGFnZXMAMaf/uy8AAAAXdEVYdFRodW1iOjpJbWFnZTo6SGVpZ2h0ADUx56cOyAAAABd0RVh0VGh1bWI6OkltYWdlOjpXaWR0aAAzMDYGh4o2AAAAGXRFWHRUaHVtYjo6TWltZXR5cGUAaW1hZ2UvcG5nP7JWTgAAABd0RVh0VGh1bWI6Ok1UaW1lADE1MDU0NjUyNjeBD83OAAAAE3RFWHRUaHVtYjo6U2l6ZQA1LjMyS0JCbYcW+QAAAEZ0RVh0VGh1bWI6OlVSSQBmaWxlOi8vL3dvcmtzcGFjZS90bXAvaW1ndmlldzJfOV8zNTdjMjA3OGE4NzQ3MF8xMGJlY18xYlswXcWJfSYAAAAASUVORK5CYII=" alt="">
每个像素点包含的信息
1.创建
class="brush:objc;gutter:true;">CGContextRef contexRef = CGBitmapContextCreate(void *data, size_t width, size_t height, size_t bitsPerComponent, size_t bytesPerRow, CGColorSpaceRef space, uint32_t bitmapInfo);
data: 创建BitmapContext所需的
内存空间,由malloc创建
width: 图片的宽度
height: 图片的高度
bitsPerComponent: data中的每个数据所占的字节数
bytesPerRow: 图片每行的位数 = 图片列数*4(因为每个点有4个通道)
space: 颜色区间
bitmapInfo: bitmap类型,一般选择PremultipliedFirst(ARGB)
2.读取图片中的所有像素点数据
unsigned char* needData = malloc(需要多大);
needData = CGBitmapContextGetData(contexRef);
3.读取某个点的内容
int alpha = needData[4*n];
int red = needData[4*n+1];
int green = needData[4*n+2];
int blue = needData[4*n+3];
一个点由4个信息表示
4.修改某个点的内容
newData[4*n ] = alpha;
newData[4*n + 1] = red;
newData[4*n + 2] = green;
newData[4*n + 3] = blue;
5.把data数据从新编程UIImage
CGImageRef cgImage = CGBitmapContextCreateImage(newContext);
_imageView.image = [UIImage imageWithCGImage:cgImage ];
有个了几个函数,接下来就需要你来指定一套规则,获取到的所有像素点,然后从组元素生成一张新的图片。 而这套规则就是下面对应的矩阵变换
二.矩阵变换 注:这个部分原理居多,若有不是可以直接跳过copy代码,不影响你功能的实现
1.什么是矩阵
若用一个行向量[X1 X2 ….Xn]表示n维空间中的一个点的坐标,那么n维空间中m个点坐标就可以表示为一个向量集合,这个集合就是一个矩阵。
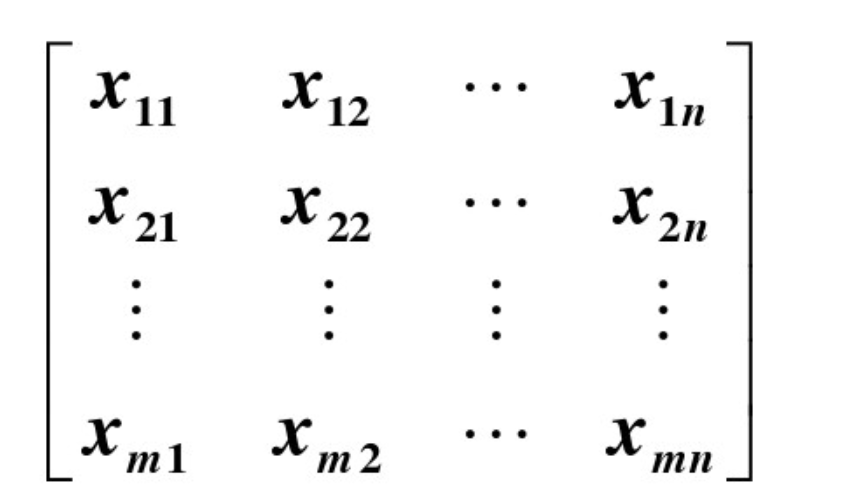
也就是说我们二维图片中所有的(x,y)坐标的所有点组成的一个集合就是一个矩阵.

BBSrvrW2aygokoular1ev1eDzuuq5pmoZhIP8eyiMFgDCQDYJBvFgs1kN5gIasJkRQcY7jQJheydOu6rldtUNGpqMtcbvqDFHLs9yuWsLSTFx17UqHxE3pF0YGBwfRtamqij4Xrwoq3rIsXNDu+oX3diMu2WhgYACcBBlkh4sjJOxGcefNE12/hALHvr4+8CUEg5C6rp/33u5dIKvJ8zxUWSaTwbFX9dXuGbldtUNGpnO76oxPu7Pcrtohs0rblf7ggw+2fKQDBw5UKhX0tjMzM+htoRAkk0l0cyCqltd3OxG9LbraZ555BsLMzc1BDAiDONK7XXTL/KGdgIdAjYBo3759iEOSQqHQ1Fpa3tW9RIgBYcrlMvQ2CAMKf/zxxxOJRD6f716hy8iZ21Vn0Lhdd
can3VluV+2Qkemrrl3p7XQO9Ps4hedB74+f3uh2EcFDtru+My5v/KyUBKUjIA6RkCciUnl64/kvNQcULW9BREoFfCQ9LDWrFbleygNYmshAKlmJK5L/SmXC7aozktyuOuPT7iy3q3bIyPRV1670++67r+UjoYMDG731rW+tVqsYqsIRP8aR0nzClnd1LxGjHAgQA73/7t27Zf8LefC1e4V2yBlKm4QCY54QBl9vvfVWSVEd7ureKVk1UG1lZeEIbQkS3nPPPd0rdBk5c7vqDBq3q874tDvL7aodMjJ91bWrtjoTOED+6EYfh98jGBfCEyKl8/N37yyKRucr5znRChFQFtQUyNa9QjvkjFm3ZtEgJwgGGkDocEtXT8mqkdUkqwxjemiOPayyls/L7aolLM1EbldNKJYU4XbVGa5V16509F8tHwmjZNBRcAQfgAAQRx8nv7a8vtuJUgaIAXkQJDNB+CY9dFuAc/IHFFIGKQ8EQwAztcPznNtX/CuKBhSQQVI4viIOIXslT7sHhEhSMODG7WoxStyuFmNyISncrjqjtOraFTqH1rZk+PWNh0Fnh9B8ZsTbXd+8pnsRMAG0AZB/U4YeytPs8SEMpAIfNNW47iFwgTmLOlMUjL7i2MTqAu/t9mXcrjojzO2qMz7tznK7aoeMTF917ao1LeFh5GoYRKQqAJZCXHKVfNSLfJRFA1+pFqB0OcFzkcVoFoceXwoATsJIAqTCqZ7jI6tJVhnEAzM1BY5IhNtV54rgdtUZn3ZnuV21Q0amr7p21bN5o8448llGgBFgBBiByxYBZqbLtur5wRkBRoARiCgCzEwRrRgWixFgBBiByxYBZqbLtur5wRkBRoARiCgCzEwRrRgWixFgBBiByxYBZqbLtur5wRkBRoARiCgCzEwRrRgWixFgBBiByxaBtuuZLltE+MEZgQ4IuAFpYpFYTSE4uffI0d2yqVs6wZVKQHtfpONjR29+2+aBdVQPpjW1ruGEP0CVJMFHPz544eJElkP6FE64lCZKqaQaASlYMRi4gaYGih+QjyOKUQIV2Sq+Uporp/qSSPEqpMFVJH5S2nBpjFtsqpSoL02G6inqqanpp59+dm1u7W03Xi8uQJ64xifHJz1BniLK58AIRB8B1pmiX0csYYQQkBttKiSXMKsEJxtm2Nsr9Oxj1ddeO3zdrs0DQ0JgrHoGt8ycOeOXw41j8EVShWAg/Jev3oW+gKmsoKX8mZLjeI1bwU8o2bcokaPAdCsQSR0eHFq/bnOpWNu351it4oGWnHwdlxlxqlR7s39NhCqPRVk9CPBPqNVTVyxpFBBoeNUAo+Djk6IKevDILdHeva+s3bBh/SYhpW37ZixWDWoDazaS20dVmj1Mpw7T8AgNXY37HKg48+R0zlOBwYS2dE6YPVPqH0r1DaXmJmqPPPztI0eO5XK5HTuuujazI7ZOoQzULc2vk2LQFZuvOhGcfPHZl9WacuWujaVSqb9/ALnV7LlYop9IuELmwAhEHAFmpohXEIsXLQQW+HtSxRiZIt4gp0if//vvrlu/+W23j0CbqpaIYoJddMV49aX91TmrOjG8/7kzZ07Mvv2OG4Z25SgOBagaMpNQdF7/hFCnEJrkJEbz8AEtHTs4+eJzL6eSmbvf+c5YHx3aO/upT31qvzX1lre+5aq7YnC+PztHyRxlUrTrug1H9x558YW9V163MZFIyQwTCYgKtYmZKcSDD9FG4Jy3ItrCsnSMQK8RAJN40HhEUF1HEbRBdPjw1P4D+669dtTKCP3JtAhuhx3f1ch4+qlXDh44Wa8php7yHN3Qk+HkEG4CTyxWm5Ad2E6Sk8i5GSbHykePnFw3Mrr7lhtj4LWAtl3V/5v/6Zdf/P7Ytx7eUzkpytWRn0uqLz433XDbiWPjp16dtbLhBmaBG7dMj2rNDDnCCEQZAWamKNcOyxZBBFzsxgXTBAqwn7LYjgsK04svvHT99buyGCoL4GhYWChgI7Nwn3v14z/+cz/44Q++457RHduvUhXLgdISkFeAvQSYCbe3fAGhMM2TUxCOHgY0tCb54INf+x9//teHDk7ipnqB7DyZBsXMwQOvntjzirgjnRTluh7GEmnDZjU3sOapJ58XOeED9Q6cF7Te8iaCKLNIlzkCLV+MyxwTfnxGoAMCgQeTOpBDoCqBiU4/P+e+/PKeO+7YrYFrfGFrIMwjFOrL9DsBrBUUgtIS0Nysc+rkZKlYRVxL41I5jrf4BWyO4yGy4CzGDutBrep4MLALyEwR9DMtTrn+rKEp2PNKcCUMMxQydKqHphZ3vv2de1581Z4IhwaNGC4xFavDg/EpRiA6COAN4cAIMAIXjoDYh6VxNajAp0q5furU6cF1oWoS2nOfPjU9silnaNZUPh+D4RyCRWuHDVgiJOIY76OgRAoMzTEA1zagiFBbEleHH6Jf/MX/kE31rVlP+QmyTMJUU/4M2KjaPxBbvxGW51QqU0LYOlAmC7WMNu20zozPnDpe2LomAznn5koDQ6J0DoxA9BFY8KMs+sKyhIxArxEo14rpJOZ51NnJsg4NJKC/+stP3/mOd4qROdgWhNrSyCjYSGg8A32DQl5Qi0eVCgbfYlJ8pfEXb988/TSe65yvjVTxx6Pt2/vWbBDRvjWCljCl9Pzzp/YfePKuu69fv10MDaYHyHFL9Tp4T6hTQZHuuvPd//zQtyDL7El7ILeOAtaZBIAcoo8A60zRryOWMEII6AbIQ+hMhh6T2ozj+KkUFsyGIWSmRlz8mX+/JOOEi2cXnF0QBXuJ0PyliEgjSbIdiAcG6qJkhaZOUrmMT61et3/6Zz9+w01DYsCw5lCsbBliBsv3HFUxMLKnkVUuYUUvpeMWjl6gaWyaJ5HmY7QRmH9zoi0lS8cIRAQBQwt9KgQYT9PAHcISoeblckMN/pDMJBgo5BAI3eQqQU5w5wDmEHYTYcA1TSoKmQgeH0SKHOWTRDR/cUA2tC6VCnnaf+DwsWMnC/nS9PT0b3zo48poyIA6JsCKmgY+s3wPshnQ4RLxvnK+RvA4gdmvUHVjo/F58PlvpBFY8GJEWk4WjhGIBAIqVsmGVuNGaNeQnxOGCQMD4fROk5YUUAt4AC+X/nrGCi3zGlwFWnp9mNeRwhsFj4kgLcjxTSWsWFI0SqZo+44tt771xmuvuzI3mHn8e5OVfXLs0AQ12XBWBOrTTbARGHDt4Aa75tdnw6zEYVGhzTMcYQSihADrTFGqDZZlFSAAOzjh9UdQDobQauR5lEwsHM1rrHYKCQaXuWI1rmAjmM95pICc5CxTK5IQ5ASrv1anFFLDaS1dozVrYe+X2LJz28j6gQf/y8GZfP1d/eutK0g3s059DmupyNOF3gVb80FV8fVinnJZIbCmibG+VYAxi3jZI8A602XfBBiApSHgwyFe4w4MzoFJFF0RU0AhVwkeQu+/gFoUO6QlnHUELQlykncjE1wWXonofJZhLrig+WIKc/DGLTKi0OxsTahGCm3b3j+U3fXSsxOP/PNxbxp39cUt2FzE6/AvEWYYg2KHdbcoBHzk+qRJ1pQC8JERiC4CzRcguiKyZIxAlBDwsZpVhFApwVpXGBU4DthIBkky85SDNEFIklpAWqCl8MoGOc3f1LxVRJB7q7dSofx0yQPlaNQ/EhO8g0ws2rXTyk/H9r44PXMmFMlPwsergVE/aHUVWLRDpfPimGQSFFUjFRobB0ZgFSDAqv0qqCQWMToI+OQroe88KCJqIOZ+NIyRufOjZA3ru7MakNCKxFwRFsHO01WDlkJt6YIf7KnHvv/dRx8bHhr66Ec+pscVjOz5VVLjlE1j4ivp2L6ObLEph0swTVfAQ7ZwTlEqCWZKwModZyGu2KuDAyOwChBo9etsFYjNIjICvUEgoOzkbBkdvZj10QlevGtnDsUrNYKVQYWoaNFMilw4UbVqQcmjsj85QFXhtaGmpaf8VEEbEsoWWKme8WY9rTgV8xwTg3xlbJhBVIBOpZqBpdRUraz3Kev06hASQTOHXqo/9a2xg684s+OK4BfwIuinQqcHqDhcsAdKNZiDY7eLmENq2a5gtomMjfTyxJ7UZkvFrhxgpXqSnOHeoMalMgJLRICZaYmA8eWXPQIWTAyaQaUNGzYcO3YMTCACVKp5XQiqFb6piVBfwVoiH6YJmuedHU+zMhlDLNoVdx07RE8/Ta/tEftnCP0mtBV3sFTKd2FvAV6ZOHO6ry+9devmoYXkYtHjT1LdKY5uxMZMIidhjxGolpWQ80zlcrmvr094GEeeYLKFulx4OR8YgWgiwKN50awXliqiCIBsEgmwTRhgT6DSrjddu2ffK3eobxK9f+i8Tp7E+F3dd2LQcCpUmAUzVTJZyw9su2jC5V2lXEvksHpWqFNBHXs77Xn4oZc8J/6f/ut169ZvxCghGM5xq5puCN3Ip/vvf/cNN7x5584rBMEo5JSE89bpaf/YyT3rRlM33rzFCM0DnWrNSCXFICP0qoDGT5/ZsmWLGHgEX87bEzaE5z+MQIQRYGaKcOWwaNFDAIuZ4mqo6EA2dPc6Xfema5984vuUJ8KiJlgegJ/CAMbRVO3b//rK6bGZckEbHyseOz5erp6uOFsSmcr2nZmrM6PwsSr2VY9Rpi8VT5h2VR0bO4nVUTGj3/OcIHAtKybM6oh27EofPPTqZz776Z07r7rzrt3JAZodD77y4D9e9+a7Nm3JvenNDbOJ0G5QEwOG0L4KdPr06Xfde7fQ20BUoDQVf/iVF+BwiDgC3EwjXkEsXrQQUOFivCkRYipt2pqLJ2PHjs1twqIhpISDZqHX18BUzWuvv2LjlmrgppVAh6UcFJ10lgzLSfZVhVtWp1qvuWbM3P3WTRs3bIKNwljp24FY+QRXrV6guoGKeaNwFE6h+37gJnwO7p188KGvT09PJZIxM6696125vn5SMLGFy1xspAt/eVgNLPSq/Qeq2PdiyzZYRMAvEUgTWWFcj1/5Zv1xJLoIcDONbt2wZBFEwNAMOBvX0PljgwssmYUdeJZ27rrqwJH967feomM1UUhcYCZFFZNFcAQOFUgYmuNbSBhCodENsbcSDBsMy4RfWFc4YB29giZP0LrMungiDkM+TQ8wUWXXYfcdwgCS8cXC3pF1gx/9kfsE/yFIaztkjjHDWqAZngLLPCSiLBv7GR6++uqrMvAui4FFrN/1qooBCTgwAqsAATRqDowAI3ChCGik21WsKqJ6HRZ1IQ9pdMutt5wcO3lmBqZ1IVuopOuYIMLAnuprVTH4B/sIsAU+eOFASYgoVCmUwu+q8HakUHGOHvn23rXr1wrSUnys39UsxfHrjudCz6nWXSVO8X7sp67AiYSHW8AyyCc0yROWDYajxDBxhU0CxbPs2Vuamp151323y0IxWaVYKBujeRwYgVWAADPTKqgkFjFSCNgwn0MfL9YwhcxEtGFnZq4yO1fOwzVDENJMeAYLaz3dgKMIMTpXLYkBtcbQnHjt/Ao2xhDfqVCo4YJ0juJJsJFF8DEBEzvFNwxMVEF5EgwUzwgXR3alXq8K5oHL8HpdKFOOU8VZxXKxyAlfoWCBMRGgMLlubfN2ES/D7hwEJkwFQ9YSaRwYgUgjwMwU6eph4aKGAHboGxwQBtqpbEIoKPiEissv/tJPf/vRbz72xDNi7yUF2/TN4Q/cfSuwcVDhZ8+PZxEJL4b+hIhCg2tHinNFr+5m18QOH5r956+/cNvtO8O9LoSHOzhBKpTyMNBTLTWArTms61SyUqaZNMTtOra11RAxkhhVLNftOc8R9AZhzAQdOVTOF2ff+a47ZEoSmzmBlkCGbDUetfbE8rRBgJmpDTCczAicFwEwAV6g8GNk6Nbbd0/np17dexD3ZbNwoYrxNvABPtIvkaAW8Qn5zMMYHamaYamqmOsdHu7fuHVkaB3VqnW7iiVNqm5ZRswKHfK5AXZthwKGfMBP4e1CNEREgIrkmLGYpiMftVKof//7+x999Nu333Xb1m0misPW8JUayoIYqqotWIkl7+YjIxBJBPCicGAEGIELRQDGBKHuE14vSWL++OabrxweWbP/4Gsyr2KhFHqvk3QERoEDPXxCl6+K78C/KqmGmXCwBFehZJbWb8pB4wF5qNiTEJQCUlIVWEGgQNUE6+AyqDw4iuvnaYnCLTnC7yoG7MTegLFEPDc8sHGLDqsKZFh1gpDPIAb8++FKDozAKkBA/F7jwAgwAstBQDJEOEQ2N+dks8ZNb73h8OGjkjYaE1ENK22pPAk2Cj/QX8SrZxhKyYbVOHiIYpgoUrE3YPhKYk9CrLOtQHnCLQjN4+t/SuIOxRS6WAC3ecJzXrpP27Vr49VXb5TsBdGMWGDCPF0Eo+6oWIPLgRGIPgLMTNGvI5YwUgjMcwN4AItpIVqoh8C7dwCe0Gj79s1Ig3VDJg2vDFihhOubvIIzkpxwpR4yGm7X6nDDiimpWOAGtqZYoYEFuVjOBPs+VcwN1d26GQ7W4f5GCAtF8SphKZPi+RpGB2E5gcVW2NJQM6lYti1LB/MZsKho3KPGYphx4sAIrAIE5l+zVSAqi8gIRAsBUBFoyQ8/qT5jfDLvYNURzPCqNhyQgxZsrD8SAW8ZLn0dRYX+ysW5GBY7hW+hqngappFAI9jK3aJk0kolM/G48DcBG3Rx6TmhQTjwY6SrimKaYuUubPpQJtgslTLg4QjLmqB91Z2agzG9kCTPyYO/MgLRRICZKZr1wlKtDgTQ94dUIo6JRKxexzJc6C6B9PqKHSjECRGaL5rUmVQoNzAah6KjYW5JnISRAj7CqlvSUCFvHz16HMbfVRu+yiWxiYzOCVh+6zrhLrhhQTE4M9JlhsgK1u3CbkL4lvUD6Rn2nNv5KyMQTQRa/RaLpqQsFSMQMQRAMs1QrtSTKQsE4tieGWtM5sTFnn0ygHya5NRIcuqeLnQr4Z7crleseOD5thlkHAcrnJxX9+/7zne+o6jezbe8ZdOm0b40BuIW5NAgPGGPYehYXCXG8RDsOqgQziAwaGjDrzlGF3WKG7oGjxQ2NoZ3MRHVKJ3/MAJRRqAtM2EsQO4qLcca5G5p8tiT55FFY1gDv0bh+gVSQUJMMrce6Oi+iCgaAqAcCIMOSK6+7Dk+UgBZZRCvh/K0q4HV367O0gMWMjVDX0JaGZBmNZNVRY7TNS5Ca1lgfiA8BpVcT7eUpKYGMTMJQz7YeCva3F/88V8++Knn0/aVCftOxUn+7t/uOVz/7H/8nY999D/eHMQwCZUvUVCqBrnEGmwLNQyveFjDNF8m3OaFI4cgsYw+n4gkaGZi/8ClB9mEuF0tFTmJGPdX7XA7b7vS5y2Izs0BU7i4GeQk+UmeRlwMUPQioI6xXU21WgUTNAkJ8rSTv9syNmGBAJAKzATxJFl2u+iW+ePHt6xsnIVsCLVaDcde4dNSSCRyu5LIoD2bpikH/dB45A8svFx/+ceffeKbr/QZo1ev351ytxlBmsz6tsqa//fPPj0T7P+JX32grJaT8ZyZMMA76di8K4p2cL/hdG5Xy4OQ+6vOuJ23XQHA1moTujn89MYRWaCMpubU7vrOcqzIWciAAHmkSMgTwjS74xUp4sIzQacvL5bySNmkSBeeyYpfCTGQJ0SS1QcW72F9tXw6bldNWJpjfc1qKhQKn/+zx5PKyA0b77li8DZ/JoGJJzNJ6Yx+ZPKpf/3St//9L33E06vwgYfFUqZiBJ6ayLZ+f5ulrEiE29UyYJR9guwf5O3cX50DY4d2peOtOOdq+RWvDX7Bof+FQoA4jrFYDClNVmh5V/cSIScCfmNCL4F2IguCPPjh2b1CO+QMh54SCqkqASgJl8S6w41dOiWrBnqSrCwc8RpAQoDWpRKXly23K4kbagqNGRWEbWehM2E3QkReeeWVeHnblZtu2py9RSkkyqeFBYNnkxvTb73+zq898z9eeOrl7W9Zryd106P+PhVnu12/3K6W185Fb8X9VXvsztuu9K9//estb9+/fz/YCFs1z87OggzwIsmtPOWESstbupqI39qpVOrll19GhwsykINUeLF7NVoFMQAuHhmRvXv3Qgz0uaVSqalLdRWNxZnLcSGMleEHBPDp7+9/7rnnIFKTxRff0pMUblcSdrRn+dMBhIT44ODgiRMnHn744Zx67xrzOiWfKU6QUqYUnPOBfrykpmWL0/Zf/T+f+tgvPODCs2vNGR25YvLMXFXFloVdDNyulgcu91edcTtvu2qrM6GHBeej85VdvyQDwI3EzkV26ayURPwOCaWCPBAGZeFrl0rsnK2UByhJTCAGgGoqUp3v7cZZyANhAItka3yFSLISu1HcsvPkdtWEDg0GlYWaklWGukOc6gndT3lYB+VRrl8sbCqCmRTP9Z1MBmZ7rq6ZxdKc53pTZyZOHT+d3dhdYztuV836WlIEuKF+8Q4iIM791Tnonbdd6Q888MA598ivsFgFmrfffju0JfwMh6okWa7lxRchEdWMgTK8wxi+u+mmm/B7E4Wim+vV6BkanKRGCAb3neAkYIVEKdhFAKRlEbKaZJVBJCi7d9xxR8sre5XI7UoijzcTARWENoMmhJcLtXbllVf+wd/tsYOip+eUuI6Nncp1mrLzRmZuonDCyGg/+fM/dePunUYmHMH2hG34QnO/7tUpt6ulYsv91YUg1qFd6ejcW2YxNTUltQGQAS5o0lK761tmsoKJ6PHx6s7MzGCECjJIVsCxV/I0GREC5PN5jHyCCUDhvZJHAiKrCVWG/g7T6RCmV/K0q3puVxIZ1BGqDAERUBQS0Xi2b98+5n5xxhk2LQ/eikx1TcHLl/TxNUPWxKmjeX/ytvtvnC5MDBB21KDpmalcbrDb9QsJIRu3q3btuV0691ftkJHp521XbW3b0BbR6NH/ytcGR7xCSJE5di61G2dRNF5dKEyISL0EKh1+cvZKHjyjFADCQCQIJmmpV/LIqpHVBNlQcRKcXsnTrg1wu2oi0/xx07TigfL9yd/+0N995gvHZwduvvbtNWXGwdxl5fTpiTOP7nnwl//g56pY3zSQmXULST2VHRqw6y52a29m2I0It6vloQrcuL/qAN1521V3m3UHyfgUI8AILEbgY7+xu2Qc+fR/+7tjjz6dS4/AMmKmOrX3xAt//D9/77b7b/Y118MvIi2A+1boMrbvWg1f5otz4hRGYBUjcHZB+yp+CBadEbhUEMj70z/8ibu/t/9Lf/r538xd7ZSShz75v/3I4dKTD/zoOzP9Zh20RK7wISs2a1INnXcCvFQqnp/j9QiwzvR6PPgbI9BTBOA9T43Dv0P95ruv/eX0T2uqsWv3jb5ad6hepFIdS5sI7sex47qODTYwlt1TYblwRqBbCDAzdQtZzpcRWAYCs169T8NOgtiTqXbi9FFY/Wy7bgsIKZ5J6cJ3K3a6wNpyQUtUdVVYqC5wjreM4vgWRiCaCDAzRbNeWKrLFAFVTQcUmy3n1Zqf7hvIZoNkJpMk3yY/QQmM4GHTDIM0v+pir0GxxwUHRuBSRICZ6VKsVX6mVYtAUE8rFvUnc3ocg3Wp06dOkmc4bh0+9n3yAjgo9zXFIcM3xJ5NzEyrtqJZ8M4IMDN1xofPMgIXFYFEaNMwN0tYTauQaWgxbLhkGCZG74xwfyYdhIQRPHBSPdwaEFu6c2AELjkE2DbvkqvSN/ZA6PEqVeyFSoWZaeFiAObJBSI4y6nSY1899K0v77dnRCI2SA2wNx3BTyA8cSzhU/Oys6WqS8cM4wwcaWu2RmVSxhWaIpoV++6RezRwEPOxwyv6XvTIzQ8SG5+AnHJVbNnqkgu/cYiUhZD+LBVmqV4lr0zliTJ5U+Qfpfoh8mdwq2vT7/3+l2dmKMAeR3CWiruKbwysLtydAQM5zmA/6XE/707qA2Lvv0ARNuL4FSl+SMpYgihLNNwFCThLRiACCDAzRaASIiaCXFttWeF+rHagxIR8T377NfiV2Lx5o4U+UazkFUcH9IGOcikfrPyF/zedTM91Zk9P5k+C9LBReUh+IqYS9tKDigC3jQFh8U67YGC7WJ3sArzA+H41VCNwc5zqsBaoEzaKTfZjdiZGead8pkiBCX4rFunXf+0D//SlJ599bq6vP2S8drlzOiPACPQUAR7N6yn8kSwczj6wD6IFCgI3OJ5u6HPj7rPPPnvP3e/ecmVc8FAYxJyHuuT2A8ez9TrYSNX0ZP/aIahNKAW6zWPfKm67Kr3+enjlAelhYzBs8EoLd2U9C1UQsmKoSdVq9b7BBPQ5hP0vTpdK5VOl5NyZk+lYffum/m2j2fi6zUns5Rq6mOvPijGwzZvW/tu/fP3GN/8IVYh6s4PK2UfhGCPACLREYMk9S8tcOPFSQiAet6rYxxt7yfukx3SMqT355FNbt27dcVUWtIQxMR1aFFbc1B3DxPbhGBRbQujvH6ggc1IrpaIzG58bs08dO/HEoy8Xp3O29+b+jXoigXWkQThu1T5bjObBZlrR+zKCPsmiqZN06OBxePK5+tabCpnhudOnvvH1737Trf7QD35o7bVry9O1wNRTgzpGKO+6c7NTnPunv33sg++9jU2u20PMZxiBXiLAzNRL9CNYtl2346YVj4mJdxEUOnRg8sUX9vzcz/0sCEAwkytUGew9Uq+7hmkqS5yrKRbK6TQmU7Tpqfyep44Wxr2BTHbL5h0vnJlJJjKJXJKUOdJMzGN1pg0jptsl0jAMWKdaiV7dd+SKbTu3bIkZOUxFrSV37RNa9h8+94//+LePffTHf2BgewyS+w7lcoTFqe++//qPvPsTH3zPbUtk1QhWF4vECFyaCDAzXZr1uvynUsR+V8K3AP6GI2bPPfdSKpXJDglzA/jGic3PM2HADT5yNMJg2RJCoVBSVeSurhvZ2H/bm+DxQEtR4Si98NQ3TCMp2ChAm2w0S7H3Vjh0d7YAOZTX/B5QqUCT47WXX9p7xx0jyICCmvCT4NOt79g28dr7n3ryuacfO3HvtlGKUaFQya6JVfLVRCx5z513P/uNybfcjafiwAgwApFD4Jz3PnLysUAXGQHsZg+1qVGoS+VpeuH5Pe++936wFMbxDNDS/I+ZVDLlYpbIsahuXfgxl5NkgA3wrNSgqvWRn6dHv3OgXKqXS7YwAgw0z3bkZJa0swiFkVZ5r2uuGG5ESA3QiROnDh48/L3vPl6G3aBRIr8kpq802rHlyvJc7PHvvjp7RLBsFjNSVE1k9PHDEz/1Mx985OuP0nTjQfkPI8AIRAqB173qkZKMhekRAgE2dpLaEjSPyTPuyRMT265JC6O5cHoJw2LTkzMY00Mw4B1
HqlYXfMR+8GKkDrZ45WoAGwSfVJM2rN+ciGdi2MBVtEfVc7Gfsrimc8CNUOMQjhw5gn3usVt5FZbkhQmKaUL3sqlSwsBj//DQ1v6NgplIqIO25xTWbh3GBdWSN3Wwcwl8lhFgBHqDwPwP4N6UzqVGDoG6VxsaHII1OBb9YM/I//an//P9D/ygWFiESSbQBkgl8PsH0rbj2HVVWNiFisvix/Dqvma1+N1jGNgxL/Bh0J1KCes4fOJULFRcNxBsJya3VNM04E4b0QWjeS2yqldIbk70vvfdvW3rjmSyr79fLP0Rd3pUPU0xi9KpXL5QFKVgoE/xHL9smEmQVm2S7rnzvke/MXn/ezJyyyhs/AhzeeyZhABTdLkH2OLn4hRGgBG4CAgwM10EkFdXEUJbAXXgAyoKfF1M/2CxZ5XgNQezNaT6KmlxQ/gUFZcqVcLcD9SR1x+1GKgmcFwbGpKmK4YRI3gvENoSbmrcugAXlBRyD86IRaXzYUF0PunsXzNccIXMBtbRtepGaFwa6CfWT74OyeMJOnjYmStM3/SW6ygtSE4lF6wjpRYjgYE+NVmwLDG6CEN5rNbCIirEw2vOlsIxRoARuPgIMDNdfMwjXSIUGsiHLtqDDR668cCKWzClIwU0gCEyxSVPaBe2i518Y7CAyCagj8ju/vVH6EYmxtvgWkcTH0FIPmGRkhhSa36aUOBekFP4NRSgeeLcSGigIS4GaeF6qFngGIWyI+FXcXXfzJHJgTXrUMa/ffOrQyPrf/jHciiwroBePQW8GigoDEZ92IV4chKeJ7bhHrBRc/PfZuTcovk7I8AIXCwEmJkuFtKrpJzQcA5jaSp0pnoZXog0jJIJDgAT4OPZflA3EykzMMBeWHdEPsy0W4VwCS0MFMQ5xBHCOSEx0AZ6E+QkiSg8dc4B9CPoIyzxnFPiK+4NT2FNLryc1mBk3hDPq0D7SQ2MprzT9OBDB4Y39r33A7cYg2H5Jgp28VyYxIqj5ATBDUS9bheLxXRa+J7D8B00J0TkPtCiCA6MACPQIwSYmXoEfFSLxfyO67mGZqIXr1QwmmeItU3zIfAw+xRqPDhbpiNHZ64aGGjwlmSv+SO2ugO3GabYU8hxCeZ+KfT/gkLg0AiDeviAfubzFWQTfhUp4XST0s49Q0hpyAHECPayMNOFUbpQn8MB/oqmCDrevzy855vfefR3fvfnc9vo5EnacBX5GqTwYBoBVRBbSsBwfSBHZsKcmZkBIWGGqclMGNaD2sRjes264QgjcPERYGa6+JhHukQFvIE5GYx9aVSrQGdShJ+H+aBYGnkOvK0WSs4Lzx17+pm9f/08RuFwE+wOXneMxa06jL9hJKFodfhpDZSNm0a3X7GDRkJOklSEbM+SU7MMlI5UsE04PCiWN51zmaCxeq1iJmAFjjkvOQyoi7viZCn03HdnT49P/eCPfDC3VYz1rd1ELqQmu0q1OCV1I+l44jIrRrGYLg0f5ssWf+Vs08IUjjMCjMBFRoCZ6SIDvgqKg9KAKSXoHzCWC/xwiCugygwlchiIC5TQmV0mnXr7269Zv+HKbT8L64iQOV5/hEoDpQpp2IQVjlntGpYTCc3mS98E8cjRPBDMotAgKuhD8uw51+ArssQRao3v1sq6bpKGjfQUsm2hQhlWflx77LEXb7vl5htuT9RmCct4DSx4mjmZzcXKbsXU05j1EnToUw1+yn0nmUzG43GpNtm2Le302DBvUcVwAiNwURFgZrqocK+mwjCJA4M7cAT6cY8SwqOQMGSolApB4CRTwvXD5s0Yqmv9TAq8fcv1T6GNglV1q1U7Lu5aRDmSjRpUJHPDNSgLJIRPGPC3QVqNBCNuhVtxhEQF5Qq2go6jeMpf/eX3P/SBd2zdIcqJwezOo1Pj40Pr+uDDyHGcQBh1CMcV2DWjUqWqXRWOz8OAfc2hP8mppkYZ/IcRYAR6hAAzU4+Aj2qxQR3W12L8DjNKG6+iePK1Uydf3b7rKsERsMLTBxLQQTT4g5jVTE9QlQ5VqE1YMAyoGtijVTS2bM6oldKqP+qXxWid4JtJTD/pmnoqadXIi1E5iXFBbCouzDBgs4CNlJAPaNIhpR9akVqFQ6PQVAEW4DocJs1i71fBQNN76cnvzv7KL9xBc8Lmwj9NKphJpU/9ycHf+v23xYy0M+f2YTTS9amKQUaq5WGSV4fOBClAS5hYQhxHEFib5+FkRoARuEgIiM6BAyPQRABdsyqMvEPjOA/MFDsJEwIZQABScQmPQgVpKEDNu88fOXr0yPj4GMbePOhFMkOLMpmErqt1MYMlEjEsh22WSpXS2Jkx0FnpBL34+OzJk3VZOuaB3KBerVdtrP9VQodJoLE81Wzaug2LmcLdnkBJMLiAmUaBNm3aKMRS4PFPLoASdAUyPDM9PTwsXSWdX2y+ghFgBC4mAqwzXUy0V0FZYj1TSBgqRsuqhM0vxsbGGnLDdgGnwh8zuhGDCZ/reSGLLeG5sPeg4umwPhDDdZhvqlG9QOVaMZmx7Hq5MplOrBeu+WB2oSqJBPYen6Rnnj324L9+ac2W/g/p9229eo1uQgJVN/W6jfth+EBTY/TIV54/fWRqIDP06v6pctmzYusmpmsVX/MNv3+dYdsbAwxICosJT1AXGMqm1w69tuOqq5cgOl/KCDACFwsBZqaLhfTqKgfdt0Ygpxvecv0//cNDYrcIaToOcpJjdJqqa/AJgeuWFk6Pn8I4YblcnzxRGD8yN3F0tjLjHNh3uFjKP/O8e2wqmxw0Rrb2b9m5Lpkza255UBlO96WtuDk7O33q1Ik1m9Jxw5TLgWNW6LVPobHTU0dPvHpmbNZxapXqmVLZK1fGYPkwXYL/1uTuu26HEgaDDgWGEhgohC0fGK1Oh48ffO99u89OZS3tOfhqRoAR6CICzExdBHc1Zo05HEwpCWsF6Ctw171jg2mqL784ft3utYKToDOBnESrEYrLMh5wdN2IY/vJlJncPjiYGtw44sRV48abru/rS8BjhE11V61khs3+tQkY9MUM4VvvLfcMrN/xieMTh9ZvG8xm41WvNlec6hc+8mAraEGkzVsHP/hD76GalkmmfeekosQCJbtmnX56ivI1uvp64fsBRnwB9tN1bRWOaRU6caDik7tme9PEYhmPwrcwAoxAtxBgZuoWsqs4X8V3fBdLg/AIsQxt2LT+6aefuu7W9wtaCsnIsz3F8lWoIEsnp6npyXo1tBoP1GQG9nuGEqP+LRhnC2kP7hxcM9TPoI35VbeSKiWVflp7BdnqGrEhFGaIdD2dTrpuPQ5P5wgqZYYpsybcSh3n1Q1ysgqcs3GYAthNxMjBjBQoFctphbsIQa6vvLrnmuuvIuF3iQMjwAhEDoHl/OyN3EOwQCuHALyAIzMNrAPeQdSi3btvmivOFM+EX5EInQqjYjAnhzOFpZcrlsXCkznIQROcIVw9YMIJzRBpMoJJIME40HM8IUWoqOUnaWz8RKE4C39IyCGux+Jiugnlz9vRQRx8oM8hE9yOi2wsxyUFlKdSDPZ3QnIdW8jXS9WJU/lT4yfufd9uUS4HRoARiB4C/GpGr056KlHNroE6DEzhSI1Ioe1vXpPOxI+eOF6cDft3GHMbmqab4AhYxi1VWJghxIS7I6y3Fet5hWKGY0h4DWZCXDAMjMbhccKiPnGB7dZzg9lNm0blXoI2XJiDd7yaH7ikug0p0JbBQ05V5BPSngqnfSrNzsGLONl1J1w/q8/lC2MTY8VaYRBrnuZ5balPwdczAoxAVxFgZuoqvKsvc9MC5fjYRUmIjgMUEaKf+eRHHn/ysdMTWFskQg0m21UYRYBbltx+7IoNu3Rk4mKLXPyV/ActB6oSvjY+YaniG0wX6MCeM/sOvJzpT8XhwAGl12txHcypmpop9m2HMSHICQwnSS6BMyHnIcOQovoHVayOgn8H8T2gfftfO3L8yEc+/kPirHDlyoERYAQih0A4Uh85qVigniEATsAYGXr8xmYUoIpwzO6dd7/j6PEjM8XJ3bfvgqtxL6B8qZgOPUEsUVaQiSSe0AURShKFhRSFjEQE5TWYSXxXKTfSZyS9vgGxJBbBNEBBzQtC+YR7PnhSkrQWiisuxNf5bAlLplLlcvXggUNQ1q7Zdd3ItgTy8CukNHIV13JgBBiBiCDAzBSRioiKGBglkz06tjHCPzGuFtLGFdeOzMxN5ot5qDpw5wC1B128mPRZYlDAHxioA7dIEhJ5hDNXDSaUzCQyFRsqoRCNcsNW/+CI2Fs9LE2D46OQPReULDJsuNoDS4msIZ08Py9hQFOTs1PTc2vXrr/y2lFBbQG5mHhakAtHGQFGICIIMDNFpCKiJQYc5sGvghj+QscudRiFbr51Vx0LVcFW4ZlMKtVUT5YgvfAdDlqQ+ZKn+mL3dfwTWTTIJIxIRlEd38PQohoSCIzrQr9EKhz6yQmns+U2b4XMIg7RpHQ4IiuRW3926NprMrlcSlyAp/DITAlRODACjEDUEJDvf9SkYnl6iIDs07H1Kz7z/Tbc/BQd6BfY4Bym2nNzZXADAsb0lhqUQMMnnAISt6II7J8RfmCmICLzGcprNNevQrfBx3Hsxm6zATnw/gDdqzF8J4gHmteiD/I6myGmmTIZY81wCgZ6oMF6aAooMuDACDAC0UOAX83o1UmvJQLpzPNDyD9hG4nFDDmyh7G3gQHhdFVYaJ/VVC5YaOhMklECcIkIGD8MPzIiixZkI7lHt7BLILYhrCt60NSTxLIk3Dz/mc9HaEnCqk98FjZs8RQO1L0wwF8rdvcQ65pUt1iF81cOjAAjEDkEFr7AkROOBbr4CMheHuViQE/M3Ei1CYYIJlUr9UJerFkVBt3gAOwruxz50OTOjiGDNEJ+gcIk+GNxAAMKnSlwMOgXko64BHpPI4Q3I4v5fBZGUBCS8QHJUTKpif3j6wRmEuqWKBdrqthsfB5J/ssIRAkBZqYo1UZkZIESs1iWeNrM9JkYIJPbRIQ7USy+6nwpckYpvGq+jMbfkOdEPIyEV4gY1uXCkQNivut7+Xy+Ugo9Oiy4LrSoCK8PD/PZvu4ZwGv4mCb8uorRPJie16kew+gkB0aAEYgeArrYwLRVwPoPwxDzznJw33VdTD4j3u76VnmsZBoWwaBoiIRQrVax9ygWTvZKGPlgEACwACgsHcWWEBBGCrmSj33Bec0vEmpUE+6DmwZshbdUiNB1N8sEG4iJH7DCwlE79O+YAwpIkwTii0E5fDBYhh4fJCFt+1SyFXIPHH716q3XqmTZJcJwIK6zZvy+gSxcjJdPz2SH+7R4kJ8Z7xvIQDEC94TlhON4PsrA9RjAy8JIXESF7kPptGiTDeKcl0rYmc+bT7z+p5YhZRN3NK8IfdIa8KPnY0QPO26IJs3tSuDTKqxUu2qV90qmcX91XjRXV3+ly5a3+Kkas83zzBR6oxFXtbt+cQ4rnoIeBEwgBYMYiECqXskDYSCALB1SISAFX2XKij/7BWYoq2lh3V0EeUAQ+ICWQAOISb549dCrO7ddsXPrVTPTs0MDa2MWTY/RNx5+6tRLRx9/6omPH599y61vyq5LwM6vVvLSfTAdD4lLPCeywPqkcDpqHuELfPzlXcbt6ry49aRdnVeqhRcsbPNI5/5qITiIr7r+Sg/Xxp/zFOIr9AC5c6g8hh5lRHq768W5bgap
JEEYMD+EkR0ujj2UB48LASCM1N5wREpv5ZHVJKtMItZteRQfjCLUJvi5kzoTwWRBre3ctgPqi4a1T3oWo3H/+29/7uXnjs5OlsxZ9/jJyudq3/iXrz71/h96193vvW14ZAc5FderoT/xFahgyEjFsicRIbWuwndDFwO3q87gAh9ccPHbVWepFp+FhNxfLYalmSLrcRX1V7qUuPkAzUi5XMbPEKgCGKeKx+PYjto0TSwoaXd988buRSBSsViEAJVKJZ1O42cRRqt6JQ96fAACiCBMqVTCV4iH7bp7JQ+qCW8mAMEritFODE8BK0DUdXmEoiS0JYzEhVF8A6OYMMzGloMbhrel4sY/f+HFz/z5l/oSo7e/9V2p6cw7b0xNFU597RtffPbJ/+vokdM/95sfLuX9FJyFq9IeIWS0eSsFbI/e7cDtqgPCPWtXHWRqdYr7q1aonE1bdf2VjpZ3VvwFsWw2CwUQeoBUBeSPJlBuu+sX3NqVKLpa9PvYlQeSgJZQBlgB3W6v5Gn2+BBmYGAAzA3xIFWv5AE+KF1WE35JIA7BLkJ9BYEoF0EwEygJCpMiZphiqjY6DFcLamWc/u8//Isd627cfcN9ft3YkL6mODubM3I/eM/wS0ce/foXv/fxH/twamMKrsE9DWoSFlGRL9cZYYESbAP91u1TFvrGj9yuOmPYq3bVWarFZ7m/WozJwpRV11/psuUtfAYZBy2BZtHhIqCPkz/GoTO1u35xDiubAjGQIfp9aAZQU8CXcnoglYJD6R4E6EmQAV2/VCshmJRQcsPFFwhiABnIAE0O2hLEQPWhOXa7vmCqhwBaCq0ioC7huyJcRwRetVCLJ2IvPHlg776jH73n/UPxLU8++1LKomOnigMj2tY37fLV+je/f+L5p47ctmELdrvQdQO0BEsKKE3CYiHM2RDbYHQxcLvqDG6v2lVnqRaf5f5qMSYLU1Zdf6U/+OCDCx+gGT948CAeJpPJFAoF7FwgmQnNVL7JzcsuWgQ9LHrb559/Xg4qoiGCJjFaBZEumgwLCwItQWkDGYCcXnjhBYkPwOmVzgRwIJJkJjA3Kg5SgbbBTwvFXvG4J1x8Q1uCdoOZJpcURyVHDfz+VPb4gfFcfPOzjx6/dsMNMcqWJv0dozeM2NSf3Kik6Pj+4xO1Wbvifesb35osvxYfCupGFfNMnqJiX0IYzsGODypXjKZWXOaFGXK7WojG4niv2tViSTqncH/VGZ9V11/p6FtbPhLGptDbyqkm9G4IkgbwhC2v73YihIEGgNIhsPx9hKPkhm4X3TJ/MCIAAS1BKogEwfAVQvYKH8wtoehmNQEZUDgqsV39tnyoZSUKWzy4fxUmdXCDJ9zWCSuGWqUyPDiUULOv7nlk8+iOEpYhjZ/eMLxjckJsBpjrw+aEWm5wYCjfX61VEklL1Wtin3cNdYosfIDpQ30KsI1t6/a5LFFb3MTtqgUoC5J6164WCHEBUe6vOoO06vor/f7772/5SA899NC6devuuOMOKAH4XSmdaaK/QJfX8vpuJ8qioQ2ADO6++24cpWDdLrdD/lIAECRqHce77rqr5/jIapKCQdlFZbWr3w7PtaRT0uePtH0I1zJhWshBpDQzl0pvqI8rv/Krm37+47/3/rtutIK1EyfHrhnc+NqxGTuhKlY5lVXHpo7+0v0/fNv911AWewDWPHI90gPCOiRLrrM7u7pqSWJd8MXcrjpDJfG5+O2qs1SLz3J/tRiTc1JWV3/1+oWJ5zwKf2UEloaA3LMPWo6WGsjNnB4z+5Vddw2ls9oTz3zDSNQ2bM3sPXnwyhsGrrkpO2UfeXbvd7ZctfbG264hzBXCdCJcbKuSi1FBhRxoTt1Vl5b2aHw1I8AIXDwEmJkuHtaXZEloQPgIo7yGyYLuiz2PMOSrZgezIqrRJ3/tp4P47N8/+OcvHfpWYnQ2r+//9otfeWrv12acI3fcf5O1TmbRmC8MFS94I3c18nTBVRwYAUbgskOgN5NGlx3Ml/IDgzx0kJMcfAuH9XQstZ04fWzdyAZMFdWm3ff8xDXV+vu+8Lf/PFF+sWTvO7XnRLmef8tbr7nr/t0f+Mg7hVWfhruxXBf5yGwwZMy/mS7lRsPPxgh0RoCZqTM+fPY8CIRm4vAU/joiwdfhkdFiJZ9OZLRUnSz9Qz9+04d+9KaHvvz0g1/94tU7c3fe/QP3P3B3fE2oLWkEn4O68E4kWqM0qIBVXqPg+RkJCzEAADkFSURBVL/nkYNPMwKMwCWEADPTJVSZvXkUaDnwYNggEKHyNExkVC0GWwa7phQNw6QMjPe09/7ETeraCSyXvvXtt8kRwJrt1WwHBnK5/gxuFV5i8ZGKkzwKt6scGAFG4PJCgH+RXl713YWnlQQSZhyO5UlymZyb0VXThR/BIE9K3g4mxsb3kllW+gon8ntryvS+oy8UvZJiafFkLNsPX+MhJ+EPLCGQZfPYBYk5S0aAEYg4AsxMEa+g1SZeuF86+CWXHSzYeXzrz/RNFcesmLJuY65UHKv6c9PFMXhk3LplI5Y0nSlMlmp17H0u+A234Q+OMiLjqw0AlpcRYATeOAI8mvfGMbzMcwg33wu9E82P4zUAiVlrZWwwPSIjqcywWd2/ITNq0TBWV8B1kpU0wU9i0Qxuxs8k/qV0mbcmfnxGIESAewJuCIwAI8AIMALRQoCZKVr1wdIwAowAI8AIMDNxG2AEGAFGgBGIFgLMTNGqD5aGEWAEGAFGgJmJ2wAjwAgwAoxAtBBgZopWfbA0jAAjwAgwAsxM3AYYAUaAEWAEooUAM1O06oOlYQQYAUaAEWBm4jbACDACjAAjEC0EmJmiVR8sDSPACDACjAAzE7cBRoARYAQYgWghwMwUrfpgaRgBRoARYASYmbgNMAKMACPACEQLAWamaNUHS8MIMAKMACPAzMRtgBFgBBgBRiBaCDAzRas+WBpGgBFgBBgBZiZuA4wAI8AIMALRQoCZKVr1wdIwAowAI8AIMDNxG2AEGAFGgBGIFgLMTNGqD5aGEWAEGAFGgJmJ2wAjwAgwAoxAtBBgZopWfbA0jAAjwAgwAsxM3AYYAUaAEWAEooUAM1O06oOlYQQYAUaAEWBm4jbACDACjAAjEC0EmJmiVR8sDSPACDACjAAzE7cBRoARYAQYgWghwMwUrfpgaRgBRoARYASYmbgNMAKMACPACEQLAWamaNUHS8MIMAKMACPAzMRtgBFgBBgBRiBaCOjREoelYQQuLgKKrZBKlquK4KqkkFE3hAiaT4pDikqBQoFOCr6WiOpEgxdXQC6NEbgcEWCd6XKsdX7mswgoBDYKg382sRGTb0fzHUGEf8ktAokTGIEuIMBvWhdA5SxXEQKgGyhFih+EERGH4tSgK3xpPglOQ5dqkFgzlSOMACPQDQSYmbqBKue5ehBQQT6Kj8E6DOrhqKqkeqRq4qsI4bHBR2CmcKBv9TwcS8oIrFIEmJlWacWx2CuEgGpjTknMJQk9ySVVCVRHUUwxt9Qgp1BTAn9BmcIRnMWBEWAEuoyA/GHY5UI4e0YgsggIMwcfupJPeqCAeVwfXKV4Ql58awSYP4RfF09FzV/BfxkBRmAFEWBmWkEwOavVh0BAgm0CsgIyAjG/5AUKDPCcxpNIcpJEhQuZmVZfDbPEqxIBHs1bldXGQq8UAphTUkjzgngQ6B7pCtUwmgfNSeTfoCXE8BXjffoCLWqlyud8GAFGoAUC+te+9rUWyUSnTp2anZ3NZDLT09OWZdm2jaPrurreGzJD0el0eu/evYZhQAbI4/u+oiia1puBf8/zgiDAGhjAsn//fsdxEolEsVjsIT4SFllZuVxuz549/f397eq3ZaVfhMSotSs/5k1OVL3yYKUy+//9/T8NrqFyeSxu9CvuqOIlVaVKaknRZiiwqD6qun31xKGuosTtannwRq1dcX/VuR4llUhawXFxf6XjTWiZRblcrtfr6HzR36GzAwfEYjFkV6vVWl7f7UTTNCE
DBAiXRAo+kO8wUrpddMv8AYvkRcgDSSAGvkJIUFTL67udGI/HpUiQQSKD6kMltqvfbsvTLv+otStFTfdlBr/3zHHXcW7fvNEwq7pjJpLJ4pSmeLqiwuwBBhEVCjzVFbh2G09uV+1aTuf0qLUr7q8619d5+yv9gQceaJnFww8/DCrbvXs3qAjKCro5MBNeS7w5La/vdqJkRBwhxi233AIxoDOBD1KpVLeLbpl/qVSCDMJvgOtCb4Ngt956K66EeC2v73ZiUwy8ElDdIEahUAB/33vvvd0uekn5R61dTdUoYdJ3HqkaOr373jusmF+ovtYfH1bdrJhdgkKuuaScJILONCJG9RI7l/S8S72Y29VSEZPXR61dcX/VuR7P21/p7X7jy3EqdHAIKAMUhyP64nbXd5bjjZ+VYmAoDwHjZs0MeyVPkxHBBBAJnC0l7JU8kAGYyGrKZrOIg5ZQib2Sp1lB50Si1q6smBG4tH/fTCJmgZwCUlPxLI62E1KSTmpQU4yCgtE8RzBTt/HkdnVOg7nAr1FrV9xfda648/ZXurxicS5zc3Ny9AyvIvo7/ASQw0Ttrl+cw4qnQGHH1Bc6XOgEUOMw0ghNDl9XvKALyRAKpVTYIczMzAy+QrxkMtkrfFBNUN2kalutViEGBANEvZKnHYZRa1f5Guk+vfTCRCYVK5cp2UfFaiVuanE9XLkEuodVBGzysNTJFGYQ3caT21W7ltM5PWrtCtJyf9
Whys7bXwlTgpb3o5NFTwclCQEXyJ8A+GHS7vqWmaxgIhgIIoGQwAdSZwJxIrGH8singzD4nQupIB5SeiuPrCapOQEraHK9kqdd1UetXZmadeQw+V6fbWtjY7S9j9LxrEaGXYHFnnAKofkVMgtqYCm2T45qa63fl3bPu9T05i8tbldLgi5q7Yr7q87VJ9t5h/5KWDe0zAJKkuQk9G5yHkXm0u76lpmsbCKGJiEMjpANnS9oElNNvZIHRUsBIExTMCDWK3kk1BAG1SSrDJwEwXorz+IGELV2VanR9x6lUp7KhdoTj81u2t4P0886+TFLjOYJPUmH3gTHRSrFVKhR3caT29XiNnMhKVFrV5C52S1ANu6vWlZih/5K2BG0vAcDQTJdRqCgyK/trm+ZyQomggYQhAYX6nAQQ4rUK3nwaEBGlg6REId4SOyVPLJ0icnCuuuVPO2qfqFsuKbn7Srw1YOHTgS+Wfft1w6dsGv9ZkoxyMRrITa+wAfTUBjKw0AeknzxY6jdo61UOrerZSAZtXYleivur9pXJMDByQ79lbAua3k7fhvKypZHyQeIt7u+ZSYrmCiLxugkFAL5AwTxbg/6d5ZfCgBAwPzosBDpLT6o5mY1QXJ8RSX2qr7aQbf0dtVcFSAbaui8LqBCnuIxMmA7h19QIIuAXEdwh9dPnkOGQo5Nt938q1/+yv8xOkqKTr5W1WnaoWnbsdPGKNGAW7N0lSZ9+qdvT1b17aYS+9yni//5P9PxqaNbB20ttknxBoUvCBwxEyViKgq6CHhyu2rXeDqkL71ddchsBU5xf9UZRODTub9qTUudM+WzjECPEDjbXDMZGCMITWZyksYnRASjbqYlHIUf2COcNuDk7pvu+5M//vbEGJ0ZB3XBuDSmEGzxsMwAqg+GhcVdRw9TraKREsegda0STExQOrnWJ9ijYiAvDGLsACPecVwsPhwYAUag+wj0ZnFS95+LS7hkEDjLRmcfCa6CwsHm5547+Q9f+OorL78WszK+p4yPn6nWt+3Yfp2uDPiudfKY/92XHr7lhnf8yI9hpSzVg4Sqp6BOgZmgl0imeeoxKsyBdWAt4lbKpW88Qh//mUGbQFZx7SwPDTSKPptyVhaOMQKMwIojwMy04pByhiuLgGSmBbM7oIeAikUsZjA2bdrwgQ/ef8899f7smpiVqlZtzYjDY/jJ4/TM087j33viw+/+4F13YRESGSaOQUyHJgROs2D+LUx/AnrsO1TNJ5QgjZ3UHS/56DdLH//JlOsNBqaB6+aZCMyEGSfeAmNla5ZzYwTaIsDM1BYaPhElBBbyEyzlKNNngFfg5m5waGPgU7lEOFpWfDxPw2uoCsr5i//+W3/w0R/78WGsUjKwMhuraOu1cMZVd+qaocbBNV6dXniGqJoJVEvXDM/NvPj8Kd+50tATYEIY/WASNiSnHKabmJmi1B5YlkscgVZDJZf4I/PjrSoEoLmEA3cLhAZr+OVKeXxiamq6CMKARTc2oU2myYzR8Hp/qpS//hb6hV965z3vG8YMUTpH03ksQnIVta6J5bOWXVOFqalPh16jMyeRfxInDcPSlfipE3PHjgj346JYmOOp5CkgJbghtzzEe+M9eMGjc5QRuDwQYGa6POr5knpKwUzJpLV2ZGBwKC1UGTE2Fw69KXTszBP9/WWi0rad+sgGKtftYrWYG0Q7r6gabsQggenYwsoOJnzPPH2A4IbIBOE4WIwAu7tCpfz9J8UkFpgJV4ttbPEJv4p9b/l1uaQaEj9MdBHgVy26dcOSnUXgrNok+AKffGFOjLDBUDzwHTfANBLUpko12LTmeo1yX3rwXwdzo55PybiVTqbnCvlwHyZY3IHBDKx9QM6lEu0/sJeUGhbVwneH2KZJxSjg3P79U/P+67H5uiA8wYTi4/hUOCsSxxgBRqBrCDAzdQ1azriLCPiJhHA0DL7AVJBhiskg8BA2rSA7+Rd/uu8Xf+JvfufXvlyZIbcqLMgz8UEtSPlOpljwwWuWZYBvUhn6t298iYIztcLJvmw2XzhsxUsDWfPLX/mch8W1InNs+NIw4cOXQMxeFUUyB0aAEegyAsxMXQaYs+8OAoZuuJ5bKBbgxFaWgC0k4bLqzCmaPWPuuvodb7v1vnSK9HAprrzEMo10Og6GcV1/Zob2vTqlaDXSxlM5t1wcIzo5V3h1dm5PMlmtlgUziSE/wsAgxv5EUMQeGK03M5MC8JERYARWCgG2zVspJDmfi4AAOAJsgSDIwnFs04iZMHsICJtc1qpwEmisGaEf/XdXf+TjV2/eKshkZo4GcwQHQ5VaPWGZjusZutaXFY4kBnKDf//5v9GHrH/9Gv3CvzuwYWjHX3927Y03v7fqUDYnh/FQCkwncLTwH/4fMOAXls4HRoAR6C4CzEzdxZdzX2kEQo6goGbb8Zjw5gCOQcAy21jMMA0q1GjDltAaQiUXvhzSJVK0eBy6Diz44PfBLxQDS08a2K5WpdFN1hmXRtZRpX64NDtiaGsxX2WlKD9bHRyIw2FEOKDnSmsIjBoSCXfyHBgBRqDbCOA958AIrDoElJiFNUqClubmqtUKwYoBtISv08VpKDaeWhmf3aurJxPWhE2v2XScaBpGD5YZZDIxK67Aw96JEzOFQjCXp1SSMmo6kzTmZmniNBkqDYGWwGUecsTKXKhKvhYg16RCYktGDowAI9BtBFhn6jbCnP9KIBAaJCwcypO0VKvBV0Mcrl3BSRMT/iuv7A3ipueYo6Pptf1QnWBK5+aLxeH0WgjhkGPC/V2oZOkWjW4eEFGVTu6ngn8qNqcM9NNGuH9V3Nmpif7MeiG3apFih5bj4V5NSOHxPIELB0aguwiwztRdfDn37iCgwrN4terGLCURxyAdPffcqccf+/7sTPG5RzOf/Kl//PLfz5ATr5aHZ2aH+uLXE60jypGH0T9janpqcvIU+CZfOEVqGdyEVbcjsdFsqg+7BYa2EpX+XFbMZwmjdIsC4Wyi8bXp97w7T8W5MgKMgESAmYlbwqpDQDTacGFsQ+Pft2/8u48+BtdEH/7wrf/h36996rsTD391D1SkuEEDfUnMKpUratWm2ZkSVJ7B3GC2HxTlJFKa4+WRRbFQK9byc4U53yXLJLdeIMQkG4l1TGEp+CpTVh1aLDAjsAoR4NG8VVhpl5XIwnYBhIJ1SRiaA7XAXyvMEHJeoFerwqphdo4+/9WvfezH7928MW7TyQOHNnja6GzFc3WaKNjrBn3s5WQkvBjlUrl1YpclH7s39SFiYGmuauehRvXFSB+oecKtq62TU1+f1BQlHCEUSCtGoJwmFXs0DeFeHsy7rFofP2yvEGCdqVfIc7kXjICYZEJDBSnAJAG/pQQ7gHCwtBakhbG4zZs392VyLmkeGc8+h+VK9V1vuhanTB3+wqHpwApvQTtvTFmFhHfBIvCFjAAjcDERYJ3pYqLNZS0dgQaRgI3kBhagIzTaAAoPnDiAcdJ9tHv3zQNZmDbgQ//2iK1q3h3vGEQcC2/BTNgj3Qh3pRX7LeEDqjobFjDW2USOMQKMQI8RYGbqcQVw8edBQDJToGPb2VBzAjOBTnAkzRB/NJWuuCIt+cbz6JnnHl2zJvXmNwkOiplQr9Q6ucbCQTiZIY4YClyoS51HDj7NCDACFw8B/s148bDmkpaDgKCQ8D7YyBEsF4R9HZjJ9mawsRIidWkvB394Dh19jaamD+/atQV+IeoOhZvSSscN8+28SUsNUeT35cjF9zACjED3EJh/Y7tXAufMCLwRBBShHjXs4hAVbsIFM6ka/AbBIKIklCKsWqoT1sa++ExN04q33/5mTD4hJQyYZNKxBaDIQ5IcojIiEkU6B0aAEYgaAvxmRq1GWJ5zEIBxXshM0mhb8JRotGCnUGeqmqFmpCPNpSe+e8SKVd72NsP3KAbfrWJKCXyEOar5di45qcFM+DOfLnLjwAgwAlFBgN/MqNQEy9EGgVBnkufANPIjGMWvBnAE7jsYxQvtHAKPnnv6oG7Mbb+SMMRniJ0uyHbrMIEIGgzkN9SmBj8hE2Hmx4ERYASihgAzU9RqhOVpg4BQgJoB7Va3bahTuqEkwDzjY1gwSy+/dODd79ldsymZpJlp4fAuoSeCAAOC8uaQ5Bq0hKzU0AiimSdHGAFGICoIMDNFpSZYjjYIzDdRySiNizCYZ2Vj8DmUOnjodKVEI2vpm9/E2qZg5zVr+vrEIieM7+EO0A+YCVNN0K5CfoLjcCyFEiE8zmcepvCBEWAEIoIAv5kRqQgWox0CIb80FZ3wWzg/lBk/AyOH+JaNI3Cdh/BH//Uv+vrN3bt36IZYW2sYwlhCXO5Bd5LtXJATljfhA1oS5hTtyuR0RoAR6CkCvJ6pp/Bz4edFACuZECQh4Tiv7/iBWiulhJtWm2p1qldJN+133nPT9isHMXmEC62YuAcUBJ0pZDIwkfwIlsI2gOERBw6MACMQOQTkb8nIicUCMQINBJp6jeqT4gpCCfmpOEfve89PXrfzJ2enRNpnP3twZu7Yhs2Jvgy++oEXYJkt0mHhoKkY+hMsFfIUqCpkq6YtRaMY/sMIMAIRQoCZKUKVwaK0QADMhA84SWx8XgstxUXKi89N56f10ZE3Dw/SSy+CmT7zQx9572/+Nnw/1GynEIiLRcCEk2laoeUDvsm85r+FF/CBEWAEIogAj+ZFsFJYpMUIgFTgJxwTS/Ceh5VKtOva3K/+r7/3xBOvvuddf3vl1Zv+5P/8vTvuorHTtHmzo6qBgT1osZWFp2jwGo6ZJt/HzFMYQEtQvpicFiPMKYxAhBBgZopQZbAoLRAQChOSwSVQm2Am3ti8L9tHP/aj2z7x89smJ6kvRzC5w2XrNuDg62LtLa73azUnmQytI87mK5jp7DeOMQKMQCQRYGaKZLWwUE0EGi3Ugk2DTBM8pYudA3OjImF9VibPH/2hJvOkEjq0K1jmmapZrld03VRUC/tmhFtjQAMTYbBo7FLJcst9lOqHdXnNtuKTVFDJWSfYzZojtar4I6AzLT6HbaICEl7MLzzMUrGcL6zrG/aqthmLV2cK8YF+x3N83QDHwlYQ0qpUN4JAlzaDfp8RbiIFzS5jCztCKIqQWPApnhwf+XiKYGkEXip84XXBV64iBJiZVlFlsajLRyAGJ6+Yp/JrShhATqAojbTxM3SyCEXMKFMwVaOy7mXQ/WcSVAw1NFMXzsxBAsKUwvDIbaySumBBNIpjX10wi6AUT4snM8hDcI8OxgQzgXkQsDmh5yuqSEJBSMNRobpGvqSihuIYMlN4Aw7MSfNI8N9LEAFmpkuwUvmRWiLg+q7v+zE9FupMjUvi22AzQU4s5VlBZZDKRswmvWyX1iazuof9bMFGlmMIg4oqJWFrvk4s2l1CKJETFwqeUi0XzHSGCragOiuOHE1wi67CtxKMDj2sCBZakTBxdzQyQUgEYUKWQoHgqjDlbMEh1wmTDqlCnT3BMUbgUkCA2/WlUIv8DOdFAGzkuq6BVbhhcMixfWG/d3ysdGqccmviVtI/OXZqlmbQ2/dZOXAB9BW
PNGzOjmG3cOQNNhhi1kq+Mxd4rIUaEMYUswNDgkig6gg9KCQbUQZi+Co4Cju5+wpUN6ooYnuPCj4GVXVBijbULSX0lS7uDG0M5b3idg6MwCWIwNJ+AF6CAPAjXR4IgJlME3Z9Ig
hasm1VVT3Vu24kNfb0dH3sZfiMGDXXbKWYTkXxVoAcMIhnYTTPi/kYhyNbEwkgJMz6YNjtAo9xJd7QdvAHN6djVKmJcURkoZETjhSCsMKTYitD8JBkQYhgQ9VSRArScQ2kgm2HmHOSoRmZT+C/jMAlgwAz0yVTlfwgnRDwPM/QoP24tXrNMq2UhR0IobH4JZp5au+/TLjPkhvbf4zeUrs2FzN0Sou80PV7obM9oc5QIoCfo8agmqSHCzkmFbVWL9WK1ZH+HNVt4QI9pZMKjvN8FYN4CBpeQhCgyC0Q7v7wFzpUUx3CV6kghReH5CTuCgPOcWAELkUE8GuMAyNw6SPgOMIYDyoHjqpQQmi6MP3FL30xfXPuv3z+t2hHia4Y/43P/vptP3rnH/3dnxZhDweDCRgDGpgWwua4oVIT6i5YJbWkT4qcNaY+MpCBG6VXn30sOHOClErjIyaSahZVDaorcLLk4OOAEtMBJUl84i6ZntiJCuXLF1VSVGMvDyThBAdG4FJEgHWmS7FW+ZkWIaDDCmGemRDBgN4XvvCF3//931ffZvmlWixWNXStWMyfODj9p5/+77Fg4Nc/9jsahtUCW+zi7sUI7vtgqABeM+CHYgkhqFerhXIik6V84S9//deH4sl33XVndrB/24c/oOqwDYQ1Oo6ayB/sE1DMMWIoN5wOS9liZA/8CEIKFSpRLjQnxCGJ5CrBtBwYgUsOAT0IN/5c/FwYiId5LWyZ5CkNL494H2A81JsRBBRdq9Xq9Xo8HsdUNuYMDAyM4C3tnTxSAAgD2SAYxIvFYj2UB2jIakIEFQctAcL0Sh7I0DJ0u10pQqFoBNlS5dHUzSPHjmzatClhYlhOWEP84R/+4dDQUHF9sV6q10qvwJzcGrY16Din/D/6nd/9lfd+UjPS5JexN6GYDqIUBZaghVxhPvsL+qubmj5g0dwsleyRg8dHXGP8mdeOFstPfOK3hq7auv3tt259+82062raMELw9AeimouLET8oePV6uuQWnZpWdbSY4SvYGbFBUY13MlTkzC6/jmjbeE5uVxdU2Qsu4v5qARgtoudtV7q8YvGtg4OD6NowS4w+F10wOhTLEksd212/OIeVTZFsNDAwAE6CDLLDxRESrmxBF5gbun4JBY59fX3gSwgGIeVv8wvMZMUvk9Uk5lQMI5PJ4Nir+mr3aF1vV2eJKVRxIMd8ypZNWzCxhKkmKCmPPPJIIpFAZdXP1EirkQ5CC0ylFNewFyGZuvLYV758RSo3mrIVF8xkkdpP+gD5lp16rd2jtUw/derU2mQ6ocZpbOaetZsrB48ptSJ+UiUy/VPHTz356c899DefDXL9Q9u2brpm5/Do6BXv/QVKJgiuK7TYtsGROThRh0daGJVjHgoihmU0yQiRkDhalrySidyuloom91cXgliHdqU/+OCDLbM4cOBApVJBbzszM4MXGApBMplENweianl9txPR26KrfeaZZyDM3NwcxIAwiCO920W3zB+/ItH4QI2AaN++fYhDkkKh0Px12fKu7iVCDAhTLpeht0EYUPjjjz+Ozjefz3ev0GXk3O12pfjhQFgoWRCaKIgtbYnGp08PDw/7qj89PX3trms/85nPoEnncjk42EvCUI7mnEpg1SgLw/C6ZtT0P/jE/7Izk9ucBhdVnJKruElVHVSCRM4/tqSnTlSCE5m0Gfj5mfE0mq47C6LMZDOvzY2BcRLx1HY9ZeTJ/P5x7cmxYqD/6p89nOnPDm8eXbd9y/GZM37SmikVpmslLZPAKl8ob01+ghjIysJ4XzcDt6vlocv9VWfcztuu9HY6B/p9nEI/i94fP70BNCIorN31neV442elJCgdAXGIhDwRkcrTG89/qTmgaHkLIlIq4CPhXmpWK3K9lAewNJGBVLISVyT/lcqk2+1qfv5FyDvPTCK+YcMGjN0J/+Q6tmm3oeOCxaH4WhZ2yQg8rMINp3BgJKfofb4aaDFTT8S0pB9odadeDxQHHvkwdvz/t3e2MZIcZx2vmel5n9nb3Tvfq+07n3Px2RfFieLzyxn5zOETig8sxyESIEB8AKyTQCgQARGfEAiUTxYI4ggpH/jAB4SCE8u28oKMjGSDYsu+xOQcCxvj81ucO/Z2d2Zn533499Rt317v9PTueaf7ZufXWs1211RXPfWrZ+rfVV1dnZI+bGSbmZmuVRYXlhfU8am0K9Mml3KSnUb7hulSo5uoNduVxYvq+mRNfsroyq/gZDNu1vlstlgotMtmKr9tx2y3kVts1aWfjozodwGTvUvTx0c9ZIBfbaS2L8cVN3mabRm07/0qaa8so1C/ch588MHLOFftCaXU6NixY8vLy/oZ61MX4wqxKa6KGNGuGhFtMkOt/913321rWvboMCILrsxGnTaLQmOeMkaH99xzj3XEKyNGdGSrRv0AW1n6VG9JFp48eTIiC9aXzaj9KtG9rBz2ltOlT61DpyeEelKlRiqdOn36tPrfCqk1M7XesruC+axR5+qn1bzW1tNqQV9+7Csfn54+MGOy3aVWs55KTKVSNyRM2Wn8z/oKeilWTdJxsVJsaj544YXf/r29Wv68Vp1vX6gvuzet9Bhvrzhtrt9dOHRo+6GPT+/Z/VcP/orJZU0hq+nhPz7z0nxr+dajn673OplSwRZE/UD186RMdlJEd8TT8/CrDVW3F5n2ykMxcCfUrwL7TNIAe9GtNk7XuRoXUgYKGZhNBIHKWoVRsyJj1LppU6a6KtFhBLmvzUJ33bysJU5ue9ff1saMJsRWja0mW2Ua05NexlhlAwsepV9Z17AN+uKy20PKFDIlLURkOrfffvvOnTtff/11c3DGnW5QWC4VTGvBzH+4bObKM7ld9//i53cUpFdzxlSziabpFo3WddVQYWZXfwq3dE6/hfDPrHxU/bFq2yy2Xqhc2Gs6Nznlcnqfk+gdOHRgzz1HM3d/xnzisNm7y0yXtTSfabkPWrlptxvvNSsL9dpiop0p5LSqnhxdMnRpIXUpkzKXRF0evBzI+6MG4ldXR5D2aji3UL9y1H4NTEK9Tv2S9Sk9cH9c7htukvZwYPxRB1obZIbs0WaVScZ78jBqA3zpC4W1wdojw7RJm4J4+k7f9ENlLRSywf4kdKh9GRmXPUEFlEnWMHEbhV8lupcfhFjpM6kJ15QCPSCkxtzd16YriYcffvjxxx9PVUpL9YpTN8WSufi+MR+YT+2/46FjkqWi26lx52xrrW93BoLppbQwRFtrvK5Pk6xufdjrlhPpqXS3Uz3fOnlnVfMYPnbwugM37vq5+00pb8plUyibjJbW08S8XH8+Q9s4KVleaXSWS+lkeSpVLMuQpmlLg7SKX0oH9q+vTJrOMdINv7o6vLRXw7mF+pUAXv4lr05LV99qRNTYafPCtR8U34szuh0pgXoD6qx4NsRoj9fiyxhZJT3wunGjI7DOlN06SyQ0+qpPj9U6zx11tJH71SXp6Zej77k9d9Ef0+g2naRTa9akiKV8abY8+8Xf/aImVX7pb/6yXqloTnh72jQvmqnM7Bc++4U/+q3fdBcFUr9EGqAeT0HNvxZuSOrx167jDh6sf0sbLQxr2nkndcOeL//zP5ha1eSSJpfud3+08oNSzva0aKz7PJNmNDiJjCue+mumE1qdqNZozLvr56WK7kJJ0qyVnGWbtq67WGxkW9+tJtWvNk6Z9mqdzAb6VaBf26dhlLTtCkiltG+1ap35bW40m7X0wHYLlLi9wbO5uaw/NbX41gBpkkaoZJXOjZ2PrSZbZTJPVb7+EkUTc+R+tWa82SLIJd37kdOZqdXFPP3rj/7qQ7/89ttvP/bYY0L36J8/evjwYV1nuAJwSYD09qcrXgClWQheCjZlZXiJsqtkWp9cR26AuqsqbDFbKabdF3CYbNEkCmZmp7s4a0ULlxf7M+3cW0YJPWyVNNWmXuDkPmKrs3LpdCaRzS829aL4G7UuknuNuJKtbNOfW5ooNuvS+NVGWVtutFdB3EL96vLPLCgJwiGwhQnoUYRDhw7de++9Gl44cuSIDtWpuoryangwrVl3dsZmv0Oj26F6Glwrt2q43P2Z6QaR5i24wqnnkjQ82NevZKpeWchmNRvQpHPuDPCoFOcqisgpEIiOwJorzOiyJicIxE9A127qJB08ePDAgQOSJRnkjdNuyDgNMkuW1E+qVSqLc3NLCwvtel2daHcxBz1NVZlzb3plU7pl1Wss/fXX/nb+/Ptu/yhtuuVcLdXTyy/c919sKEsiQ2DrEkCZtm7dUrJ1ELA6pPHYarWqJ5zU9VnHSQOiKIWGpEijgOXy1Oxscds2J+fOaMi3WhoX3Nbqd530TJRGWDPFQifxj1/7+gf/9WOti1dIZQsmYdePlbINSJogCEweAUbzJq/OKfEqAvZ5ON3aUZhuWV/143HqeF1aO0i9n4WFV1555dlnnz1z5synk7n9N9zQqTc11nfx/Fwhnb3x+v3vPP8fc/Pz/7fv1j3bD2jWYELzHpJGf8WE465xzgaBiSeAMk28CwBA94BSKWmSlSU9BCYkdn9DbDrttpYD0RQ+dZh+5v77b7nllvfff/+T8+oo6dmkZrvZypWnTb3x/f/8/u6ZHXd95ugnDt9m1F9y500ohlYy7/VfwL6hPIkMga1JAGXamvVKqdZJQL0lTbPU3SZt9hSN713dnEYtR6NXXriLgySSmrJ/3Z49+nOn4fXX+XXOX9BL3ZXFW//+vezNe079wWmzc6c7D0IT7dwx9USj2czmdMAGAQismgILDAhMIAH7LIVkSXeYtGkig8blrkKZtBZUqVDMaMl5Deu1O5owLpHR9DxTWzClkis/2YSdeHfwrk8dPXXKnViu5Vmb9Ua7ky4V23qZoJPSgq39FSAmsB4oMgSuIECf6QocHEwaAY3jqcj69J6VVp/JPjS9IRR6aNe7z6TkHDt9XElMFd3nYzVCWC7Y9wEePXm/ael5prwrThk9dus+1KvxPD2r7d7sYoMABOw4AhwgAIGREei/VanT/e8f/HDpnXfdXPIFszJdwl2etT+ep09dJHKdOLJaIOExI8Cs8TGrMMwdMwJaba/V+5ev/v1f/PGf/us3njQLNdPsmotVdxnZ/l+q5b5jqdA1xa4pr15aaczKibkQ2EwCXKVtJk3SgoCfQH92QzuTKu6c3XPzAXdMT+v45bWcXj+iBvTsnz1N+2wQgADjB/gABEZKYK51cWbbzOe+dPrYbzyye+c+TUhv9JrprNbDc29L2T7SpUmBfTuuWNdvpJaROASuYQKM5l3DlYNp40+gvG1asxu0ZN7OnXu0s9iszlcrVpZUOP389OfdanInY7BBAAL0mfABCIyUQLqVaJw/r1npueuuM512Nl0y+aTuPPWXJO/nbHtM3qdeCMUGgYknQJ9p4l0AAKMk8OFLP3jrzI/ct1u0E3rtulnUg7fqOi1fmgGh0T3Ng9Cn/WPa+CjrgrTHiADKNEaVhanxE1g9X0Gjc96f7fNc/OBDV3g0++5CRY8pff3PvmKe/tbh+uKffPb40ov/Zq5LmdnkuaVzte35et5p5pMdrfaqhfLy/T/tX3opVPzFxAIIxEuAuXnx8if3LUKg2WpmnczM9u39xR2SeoXgmy++eNttt+365EEzd950uu+8887h6hEz5eTS7tO1dvN23LPYIACBFQKXfxorIfyHAAQCCQT9YLRyhFZ01cvPK+fP6+ROr/vt73znjrvuNNl874dnm7VmKZs3yZT+pkrljvte2/5qeavzWd0dWx3OPgQmj0DQD23ySFBiCKyPgH4ztoez+sejxY3csxNGr7rXf63uun379vSuXWap9t1vfy+dSl1/400mUzDdZDqZ1umahucq0eoJ4+vLnVgQmAQCjOZNQi1Txk0jIDmRmkiF7MxvT5z01gx1iPSdu4CexCmX/dwvfd7NdW7h3Ll3j9x6xOy9wbS6ptNYNr18aVbfuOdaZeoLnfvS2xXNc/fYIDDBBLxf1gQzoOgQ2AgBt6/T15W+lKycqZUdEtKdhtGrbNstk0ln9ZKLWu3CM9+tLFZ/4dTDpqAVxzPGySbabodJPzxfh0lS5/a22CAAAXvdBgcIQGC9BNTLWTUE54mT7jIpBbffo79c/6GkhGnWlr7xxBPZfGH25M+7v7W5eZNMF4tl0024srQqHZv7moD1GkU8CGwxAvSZtliFUpxICOhJ2Ssv69r9N+E6eiFT/8Xtkp0L//tWu9upNTo333KbKRTM+QsvPf+Cu2heKn3FY7YrEqX/9JkiqTwyGQMCKNMYVBImXkMEVoTE9njcQbm+cQW920Kb5kFk0u2lJb2iacdNN/3d419tOMljJ37WpJKmUpuvLlU//Kkivff+B/4S9VOhz+THwvGkEkCZJrXmKffVEbDK1NcQq0k2mVa7ZWfl6VCvb5de9WpLjVZrx/79U488Ylqdf/rWE3sPHCjt3tNqNffu23N1mXMWBCaEAMo0IRVNMTeJgKdMdmcl1ZST7pqe9MnVJP3V6x3Tu/nQxy606mapMv/aj1oZ57Y7j6rz9O4HP3Hn9a2WtZVENOd8ZZf/EJhoAijTRFc/hb9KAv0+k86Vvng/IT3SVKvVFChN0pO2Tql04uQDd5w48fyT37xQX/6133nUlAoSpJndu+vtgRKELF1lbXDa1iPA80xbr04p0SgJSJNsd8fbWcktYRJ2QM/JZbvLDQXv2r9/1x/+/nsvvrjv1lvMjtm26VWbjUwuKzFzpU3prCicdhJ6VcZKUvyHwIQTQJkm3AEo/sYJrNaklf16o57L5pxM2k0ukehKZiQ8jaaG7/Ydu8c4mpJnljqdVCanRWC1pLgVJ6mR23uyUrdxQzgDAluVAFdpW7VmKddoCHi9HCW/sq9fkdbNU0AqlbIy4y5W1O02mo36hz+xbwY8vzDvODnJkDpTi0uNlVMvG6lEuM90GQd7k00AZZrs+qf0H5mA7fDktPSD7jB1OouLi9pJSqJSyWy5nLt+r2lpGK+zbVqjeW4HSQtAbCsOfD8g95k+cmWQwFYhwGjeVqlJyhENgcyAbCRO2ZT7UyoXS5e+Tq+8OT2VNRlXh3Se/1Sdpr+Vi8OEcVbOGZAFQRCYKAIrP4uJKjSFhQAEIACBa5gAynQNVw6mQQACEJhIAijTRFY7hYYABCBwDRNAma7hysE0CEAAAhNJAGWayGqn0BCAAASuYQIo0zVcOZgGAQhAYCIJoEwTWe0UGgIQgMA1TCDweaZ0Ot3ruQ+qu0+zu+utuA8U2s9YimOz1vsFstmsVieTVbJQD967bxyIY1PWMkA5y5h8Pt/Qa7avAT6Wkq0ymRdjfQXVCX4VRMaG41fD+QR9i18FkRlTv3LsqiprS6VVk9WuSZysPtkI2tdT7msjRxAiBWq1WsvLy1ICT5BkT5D9ozbJwyIDZJWUSebp5xGXPVoXx9Mh2aatXq/rMy57gvjjV0FkbLiqzO7gV8NB+b7Fr3xAfIdj51dq8Af3OdTM6dJbn+5SYKt6TkHxfSBGcSh7tMkea5KykDFeczyKHIek6dW0tcfaZk0actaov5IZykIm2eqTisdYXwMLi18NxOIF4lceig3t4FfDcY2dXzlqvAYWSSNU6h6pPOoQaF+fWhlMIZ4qDDxrdIGyU5uG8tQvUe/EZiR7Mhn/mi+js2F1ys1m06KwXSWBsrisNqyOGc2+rRr1k2xl6VOaJAsFLRoD1pkLfjUcFH41nE/Qt/hVEBkbPnZ+5TzzzDMDi/T6669LjbZt23bx4kWJgZq8QqGgmPaGysBTRhqoa6JSqfTqq6+qwZUY2EEqtbxxjVbJDImBiqyds2fPygz9NqrVqndtMlIaaxOXZitQYxq6gBCfmZmZl19+WSZ5Kr72lFhC8Kvh2PGr4XyCvsWvgsjY8LHzq8A+k1pYXW6r8bVNvxUDyUNc1+DWEuWuTfuyR8YIug6HV8mIvrX2iJJlIjMEyrswGVGmQ5KVPTJGWKxa61Am2Uocclb0X+FXw5njV8P5BH2LXwWRseFj51fOQw89NLBIzz33nJq5++67T70lXYarq2SvygdGjiBQ7b69yaThu6NHj+oSQJnKHeMaPVO7b6VRhk1PT0uTxEqB1rAIgAzMwlaTrTKZpM7u8ePHB8aMKxC/Gk4evxrOJ+hb/CqIjA0fO79y1LgPLNKFCxdsb8DeTfFkKSj+wEQ2MVAtvhrcubk5jVDJBqsK+ozLHk8RZcDCwoJGPqUEkvC47LFAbDXZ20t6UZCMicueoKrHr4LI2HD8ajifoG/xqyAyY+pXgXPb1MapUdPvRN1AlU2fau8UYlvA4RRG8a2yVruvDpN2bL9EXTr1CeKyR2W0BsgYmSTDrCzFZY+tGltNsk0VZ+HEZU+QD+BXQWS8cPzKQ7H+HfwqlNV4+RVrQIRWKBEgAAEIQCBSAihTpLjJDAIQgAAEQgmgTKGIiAABCEAAApESQJkixU1mEIAABCAQSgBlCkVEBAhAAAIQiJQAyhQpbjKDAAQgAIFQAihTKCIiQAACEIBApARQpkhxkxkEIAABCIQSQJlCEREBAhCAAAQiJYAyRYqbzCAAAQhAIJQAyhSKiAgQgAAEIBApAZQpUtxkBgEIQAACoQRQplBE
RIAABCAAgUgJoEyR4iYzCEAAAhAIJYAyhSIiAgQgAAEIREoAZYoUN5lBAAIQgEAoAZQpFBERIAABCEAgUgIoU6S4yQwCEIAABEIJoEyhiIgAAQhAAAKREkCZIsVNZhCAAAQgEEoAZQpFRAQIQAACEIiUAMoUKW4ygwAEIACBUAIoUygiIkAAAhCAQKQEUKZIcZMZBCAAAQiEEkCZQhERAQIQgAAEIiWAMkWKm8wgAAEIQCCUAMoUiogIEIAABCAQKQGUKVLcZAYBCEAAAqEEUKZQRESAAAQgAIFICaBMkeImMwhAAAIQCCWAMoUiIgIEIAABCERKAGWKFDeZQQACEIBAKAGUKRQRESAAAQhAIFICKFOkuMkMAhCAAARCCaBMoYiIAAEIQAACkRJAmSLFTWYQgAAEIBBKAGUKRUQECEAAAhCIlADKFCluMoMABCAAgVACKFMoIiJAAAIQgECkBJxutzsww0ajkU6n9VUikdBnu91OpVLaD4o/MJFNDEwmk8paJmlbXl7OZrOOE2j8JuY7JCkZICwClcvlWq2WzLNGDjlldF8payXuVZP2e71es9mMq76CSopfBZHxwvErD8X6d/CrUFbj5VeObdHWlsoKksLtjpo5Gyco/toUNj1EjaxaXmuPzNCOrIrLHhkjA2zuskqbVaa47LG0bTVZRArxLNz0urjqBFfbpkTwKx9J/MoHZJ2H+NVwUGPnV46uNQYWSf0AdZL0lf3UoY0WFH9gIpsYaDtJMkbKL2OsAOgzRntUOhkgY2SSKl6fConXHltNtsossbjsCap6WYhfBcFRuGpNn/jVEEQDv8KvBmLxAsfOrxxrsVcAb2dpaUmXIeoKaJwqn8/X6/VMJtPpdILieyeObkcmVSoVGVCr1crlsi63NVoVlz1q8QVEiGRMtVrVocwrFotx2aNqUosvIPqJarRTY55iJURx2RPkBvhVEBkbjl8N5xP0LX4VRGZM/cpRizawSNPT07YfYLsC9mJcl3JB8QcmsomBamrV7s/MzMgSyZJSliqo2Y3LHq/FlzGzs7NSbpknq+KyR3yUu60mXUloX4bFWF8yYOCGXw3E4gXiVx6KDe3gV8NxjZ1fObZFW1sqyZIu39TgalMbZy/G1WcKir82hc0NkRlKUO2+egbqptgBNHXpSqXS5ma0ztTUT5INavptt1KGWQutNqwzkU2MJjNERjaoJ6feksxQ9ckd46qvoKLhV0FkbDh+NZxP0Lf4VRCZMfUr58knnxxYpDfeeEM/kqmpqcXFxUKhYJVJzZ9tfweeMtJAtbBqbV955RU7qChHlExqtEomjTTfoMQlS+q0SQwkTmfOnLF8BCeuPpPgyCSrTFJuVZyskmxLn4KKEEs4fjUcO341nE/Qt/hVEBkbPnZ+5ahtHVgkjU2ptbW3mtS6abMyoBIOjD/qQBmjHoByl8H2+kifVhtGnfXA9KWIAiJZklUySYbpUEbGxUf3lpS1V00iIwlXJQbV78BCRRCIXw2HjF8N5xP0LX4VRMaGj51fOadOnRpYpKeeemrv3r3Hjx9XJ0D9FXVQ1Map8VWTNzD+qANt1uoNSAweeOABfVrDRp3vkPStARJI1bo+T5w4ETsfW03WMHV2VVlB9TukXCP9Cr8KxYtfhSJaGwG/WsvEFzJefsUaEL7q4xACEIAABGImgDLFXAFkDwEIQAACPgIokw8IhxCAAAQgEDMBlCnmCiB7CEAAAhDwEUCZfEA4hAAEIACBmAmgTDFXANlDAAIQgICPAMrkA8IhBCAAAQjETABlirkCyB4CEIAABHwEUCYfEA4hAAEIQCBmAihTzBVA9hCAAAQg4COAMvmAcAgBCEAAAjETQJlirgCyhwAEIAABHwGUyQeEQwhAAAIQiJkAyhRzBZA9BCAAAQj4CKBMPiAcQgACEIBAzARQppgrgOwhAAEIQMBHAGXyAeEQAhCAAARiJoAyxVwBZA8BCEAAAj4CKJMPCIcQgAAEIBAzAZQp5gogewhAAAIQ8BFAmXxAOIQABCAAgZgJoEwxVwDZQwACEICAjwDK5APCIQQgAAEIxEwAZYq5AsgeAhCAAAR8BFAmHxAOIQABCEAgZgIoU8wVQPYQgAAEIOAjgDL5gHAIAQhAAAIxE0CZYq4AsocABCAAAR8BlMkHhEMIQAACEIiZAMoUcwWQPQQgAAEI+AigTD4gHEIAAhCAQMwEUKaYK4DsIQABCEDARwBl8gHhEAIQgAAEYiaAMsVcAWQPAQhAAAI+AiiTDwiHEIAABCAQMwGUKeYKIHsIQAACEPARQJl8QDiEAAQgAIGYCaBMMVcA2UMAAhCAgI8AyuQDwiEEIAABCMRMAGWKuQLIHgIQgAAEfARQJh8QDiEAAQhAIGYCKFPMFUD2EIAABCDgI4Ay+YBwCAEIQAACMRNAmWKuALKHAAQgAAEfAZTJB4RDCEAAAhCImQDKFHMFkD0EIAABCPgIoEw+IBxCAAIQgEDMBJynn356oAlvvvlmo9FIJpOO41Sr1ampqeXl5VQqNTByBIHdble5nz17tlAoPPXUU8oxl8tZCyPIfW0WsiebzdbrdX117ty5Wq0mVp1OR59rI0cTotzz+fzi4mKpVGq326+99posDKrfaExamwt+tZbJ6hD8ajWN9e/jV8NZjZ1fxdaMDufItxCAAAQgMLEE/h8DN18pA4WCQQAAAABJRU5ErkJggg==" alt="" width="241">
图片和其中的某些点
2.图形变换
我们对图像的常见操作其实就是对图形进行评议、旋转、缩放等矩阵变换,实质上就是改变了各个点的坐标。
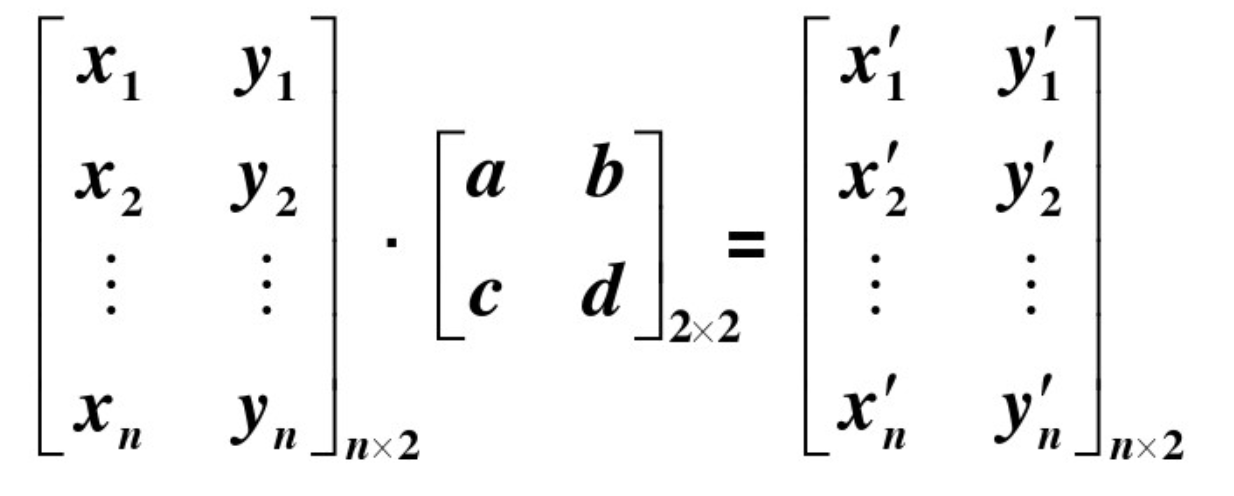
所有的图形点由老的x y坐标变成了新的x` y`坐标
3.常见的图形变换
基本的二维变换可包括旋转、缩放、扭曲,和平移四种,

CMSBnKTj6O9cZNX1ps8iZYugYg5aJEpgBoDIekk5t5/4ok/ds9Z373rpe/7tZe+ZNdZh173sl1n/finf5iIKz744p9PbugDoSZ/9dSpCjd53MkUgetNHlAJlmf8b7FYLIj1YrFu2HlCoUJEWSIib2mg6QVBcgKQ9kDQC6JYzP7TySf/wT/v+fU9ew7dfd2ePXs+/QHCD86/l4g777nugX/p84KYW1r0XxBUQJsLsB3cT6wSUeQCagNTutrI1IjfEx+Zmrr+/tRD8SQ1rplkciH5UCqZmk1+JknE9GcWRoWBoZTuUYaB/dNu5NagMHB2bnHh2IeBz4pboVh+wBqbbN9YfnNujYrlQ8szEiOXZ3jd5RnWDVNTg8LApeUeIhwGOp0wUJVi6sblGaG8fKlUamnNUqmZSwP1LBE1E2LFAlLQTOgBKGgmdCuEa/dOTdGEbGm2MyGbXeIJGc+85hdnQcwHBOvNLs7zhIysS1kuoKoAtRYRJS6gX6a5OlGmeXOVOEEYONlmrWPsVk+TLx2PJr+e0h3Y5HmyXzSzmHrLQK9OmOHJfhpz8azWney3tWCy3/Db1nK3bS2H2hY3peVQ21rmxhaZ7GdlF3cNTfZrfVIjkmBHUiMxQjdp9kuN5Lgn9k+N+D2xT2pkGT3xNLeTGrE5NeKGUiOVwWtsVtZGfE+Ui1v1Oj0GyzOOW098TrnVEwb2rNKN5uVl/vL1r75b/bKB5NbBUdlAbUQY+HVOgCP7rGuciEYCPM35bkcEbkiAA0WHoPLo1NSgBPj8kk/0JMCXgwR4jvPdqg5MWEEBxW5enj8XtAuFiqZWCGP4XJCOQTRMwrZgQUY2v2IJpNf2DCLyN0Tcmou6NbfBrbluXr7NnwtwU1VHAZLMnwtAZCZYKNV/Vn3vptrW6ogv+0edg7j3eIWBzym3er6QNSNfyIzQhMzt5uUf2YJKHDyr5o/CGu+lkrqbtfxPtCLvper/UViJDj5L0cFnacPgEwoD7c6mrg0fhbmAUF6+0WgUzVqjUVNkoFcnI
iOS2EgbILQKiQ0B0NZAGFUSS4/6Q/X+yFB9wB+q9wdD9YFgqO7k5XHrOgqoyS7QLAYFNPutly/0D2x61stvRdsKb8kda0I2crNW4NYN7lP3P33kyJE77iB4+v6nCI/cBbj1wadB3BoQrPf0g3ccqf5qePDZzFECg936nrPP/t6zg8sXv68r9yXOGdMtTDEyGoL8XBq4PsWAWHGBTp1nAIC8A7QrwEenjvL6rhJPMYBpBbg+xQA0+07IgNPj5eXdR74f14sYXhSIPp7jE+dEaJ/4AWesvPzEs+rQarcNawNrQWQwfFnZhMthJ3SLO1Ro+5HRXe3mrzu1MgFR48HUX3eqHlu3tuBQj7E+Cg/acdfoG0EMWGrdf8/+hh133RzE4MGH025VAYkvwwZKSLu1ExAtDeilOSsGyHlA3WK9MvJ1vqEBFArI17GeogNNOTCsikDVDQzbEkTXYcNqoNfqJikVRbHjOUXJeaZMmHSJsJIkyroAOuZATgGcGAhBg5y0OoZYPEx03CZCYUNNgl5CZUMiZcM31LkAGLpx/M0UuQA25AKKE+Tle9bYbHLbZE8YOH5e3jyKJn8cdq48625FJ2Rac8iEjMNAefR6eb8Sh6yXXxu1POOJYKcHbxGxUv4WERJdUwIR13gHB0CLgUiY2PXh7/TobhGxultEXD0BItY1dOIgeIvIBkOBC3ACvdC2Sex3EXm/i9vq7Isp8n4XReUNNdX+G2qKvKGGd+LYbIh9MXmJd+JEN9QUeEONowAFNkQBLdcAet0dO7Wxtk2GJmQ9SxbN/tsmzWhPNKNjIq87Lelj5+UHNfn+8ZZ5vE6U+n/g1vEZqge71Q0D1Z5tk9LWbZtM9WybHJ6XX1/MstpsrqarwPXFLCQ2KxYIpx5azALCxWKWVXOFMKuzYQ6oZYko8SqYsgvCKAaGLRWEUlntGDZQwGpBZsPuYpbN5OWHveXXxnjLr64dk7z8Vgw+PW6tTpCXH7bUune7d/8wsHe7d/e91R743tr5ZCaTKXsEGUsBinmClggxZwDNClAAVHSgk2O9FkHRN7SAXjHQSztArRAQbRNoyIFhnguQbTZso0QJYqPPUQKSAEw5OBEghSMCRBwlYG04SsCKHiVg8RkE0Et2jxLwYhYMze5RAqyXELkA/ygBPrxAYkM+SoDPFmj3yQYWxlxjM+gQtVokDLSH7PMZ7xC1iZbDjrs/0ZjkdbpqHi+37M241f84w9GrdAccZzhmGDjqOMNXfD0498XU0p0DY3LJ4MCYaiJ0YEwChOhAjudw7gsM07oOQz4wJh1Pdw6MqYZOmrHY0PNPmsl1DoxJa141MGS94svWj8r8kZ+69NJLL7uc4NLLGV9/GWOXuLxLXPb6KHF5f73onTYUELpT1PCnX/GM79b/fYOuZ57pwaMgtsDwG19ZW3v+LN3n3fqWc+ub6O6OvzfI0KUAAAAASUVORK5CYII=" alt="">

XMLYmYW3LIPqmSCoJ2EgTlYAaygqATCeKTn//vyZMnn/7LX5+2428OeCYZnnXAcxjPAZ4l8YwD/veun1qxvnnRey4x2qWXXlJ4vPfd/7diFWErxToHYr0GRdfmsgEbPjEAAAAASUVORK5CYII=" alt="">

KEYojzpvx2E1Op3SSHZaAiAks1MAcohAzkXZKQLxhw990aGzv+orzz506NA5X3bo0Nlf/tVgRuCLvyWjdGTHlKGkjIjZaU7G7JQAJ1LRMmWnpVHnvd2lgYlKbFx26Kxnf/23ftN5559//tXf8Ozzz/vmHwHzPALnfdsF6qQXsvknkhbLtxJNXv3nf3nJc8Icz3Fc5jhqPgfCZ0H8n33lWw77E5q8uPueOG9Yyiv/uHzNhcUTKysrqyfXQNfXQdY2VldW+Dsut48cFut7CSvdE5vBxJ4opnti4+I/2a5cs7R5AsPaHIa1iWEJd1wePn7tBfle+oVsrCfunAYaBRNHi8dQzHw0+BDAASdKA3MCG2s8GmucS96pWc7SRevFkyefOAnHE6Qfgf8Kr/2+wtbxI1/z0Q6ONd5wrLGjwacQpYEIwgjEzjvxh7tyvd73pDocPErJ6QPwZQa6HgK7A2ZfaIIqJgLp0ocq9bJw3dLaZnFjFY6tLdSN4upq9l1vLqyuPHnkuX6l3jfbcElTgEvqHQMvdBVWtOz3R51XFk0DxXQaqNz+p3hh87oLj2+m2tbmxx6Gqt186ugF4lyzgfs5Jqp/+RlyV4X2VRxr8jzYxePXHrYPekysPf+9URrYumZp68SksNbXn7z2cKDvLju9CQcOR0ENUbo+qi2hmihtB9UqEcCxpkdYufgRBPVquXH10ubm6ur6OjStFWxb3B2Xc9jYTq59/MgFn6jANS26pBSgejXmSzJSzquJNJCmxmmSHWU4L+8PpuF9M4sgz49Ow9veJe/UHRuB4V50UbG4MeiJG9gTryhEXXPrxNFz/0odTMP7fDQNz+bl/eG8PHPeWfRxOlaJvUvfN0xstsPrLzxxIq7E5Y89nMVK3FpbWXv86OEgVYn7OQE+Fpb8Z//KXjGs1nUXnlhhYeXf9eb8IKyVzc0jh43TNwcxFlbpNz6bePOpX7dUXGFN/nVX8MOw1rag3RtRSXtJA6cMPmNpYON7Hk3OQVSvuWjteKonUlgn1yAuW1xw8Dl2Q02SJEGkL6IoYogaBgxoAqpLIFOir69o6hc/pAwBJ0mK/JyltbX14hPr6+u5170gB3+c3Ciurxc31lePH/32jzbhPMPFC3mdSkKxTGnUeY31xFt6ut7J2KquqwUUm+sA4H0COoiRAaAKDoJ89K0agXXJb7YHIMjD33WdpaXi6tYTW1tbhZ/7/gL8sbEBsg5g/fiRc7JdXfUEFX0ZKn6axuJ8Xh11Xpt/Xr4+OQ3sPf/9o7l8W71+afM4VuLaX//NZlyJCD5+9AJ7+kTSHublx9PAf/v31JuPAs/7E0WIgnv9a7mRsFbWTlx72DqQOYjunX+OZ4y8kMFzoriJTf4F/GhYK1uPHzmstfa8Sne+NHBwRpUArtKtXH8R5IXCsCdCiJtRWBub0B9ztUXSQMOw8i6tEkIx87g0KG8y4BZQcyEBXIDkEfBh8AHg04okBDxvGIG/tLRehDQwT4PP1smTWzQkQXYIeeE5H+lA0QUv9pXDJU+F2HkiDaw0GnVXbjYaTR5F9uoAnA6BBkjJBdD0dQRCj9ZvoVm69KEqgDat30IQBKBV4eqltcxvvb5QLBa3Tq4Wi6sb62AWnygWVx4/8lyvCr6kJi7XwktUp4nOS8x5deoCz2lpoJJOA6ltuYl5eXrZt5vXLH3ybx8+kWpbG9junzoK7X7Oz5wLLc8Y74ljE+CQf1098pRnYa2sUn88DevlE2G1X/gB7BpUGLXcXm1oXv8VP6CdOnXqycc/d+rU5z75d2CeegrlySf/4y3foanzpYGV0aWfio06su4UNaB1p2a07pTWp1780gf/871v++W3/8Xnf+VtD/7qF77wa7/+4Ns//0EA7/+vL/nSa38Ujh9jMtSj137tMz5Rj9edWqiJRa+VRE8cXSEhjC/PsOPlGfEqXfPnX3Tlf9951ZUvvu1TL77iyhd+6ENX/eCVl33qtqtedNmd3g9947lwPPOZqM84lymCc859ienHq3RTyzM6M5ZazzWlW8a2VS4jKFPbAvX6AKpOGY6OhurUQSoumpIIsi00dtO25g5Liue3osepHM9vJTY92PRWPRg146fnvoa143r53S5ZnLVKd/JE0s6fohKzgXJqNnCwwDOeg1gggzh2Q09RFDPeDqGbqKaW2IuB6gYEaC8Gj6ZjoHJd2ouBpm0TiPZioGk4qIO9GGgGHqqg0nkoIvlK7MXoxWlgTdPUjK/BUUDxMyoAzmHARqDzHph6QQQ18jqYgqsPgZXHM0yTgAUgKKBpCqBq3gAgItA8HkHGoKIROLw66rydqsTmfGngbipxV98T533KB4tPgB/EZq05wpL3M6zdpoGD5RnxR+Epq3SnLM+YuVmrZFlBzrPgWEZxcwECF+0sipdHkDEJGCB+ASTgQtSsjYDOEwQG7GyAgMMLCz6YBp0REsg7sa8Mgdg5+xR17CervV7TlXtwcCgdtwnAUxmQTQANXwOzwbdBpbABpi02hqAroGkFqIICoM2jGdigzbALoIagp/kIzBIVjUB30JcZO29N3fTQmJwGauk0cHzTAzW2xTY9zJ8G9hb7FHW6tojsR1jO/od1E6YcRg3VRKkZBBQGejZqIKG6FZAmpS2aTKAFUvfQVDuoHoKWGyc2XiqxKTsNVnTXQrVj5+Xpm7UKtFlLmLVZK8+xvVlTNmtxOWfiZi1z+mat5PIMSM0SAbcNBFbibvnbw7u1Hd0tb5vu1nZ8t/ASVSXQH96tbVlD7DXpbm2zNNBP3i08w4+d7/0V4yBWJJ15YS20z4f8z97ns/dlZcduaLTbbVMFaXMouonq6gx0QlRPZKAkoPoWAQUBj6ZBgJdAunSe5aMKJXah6KCGMgOaRyB23ojHxHYQaDlHDAIxi+LlNAAZj0AA4ucRcO4QBDYB3gSgFawhEIWQgAHAKiAweTwvb+M1BTEFyJfLaaPOu/NX4txpYCmVBkp7yOX3uivqtK7SPfPCmpwGipPn5aes0vUTaWCZ4e7e0kBoajmHmiGKl8O2l/EYcAhwLoGohSPgQ+wPEcAGHQgCAmryBoGQx/MK2MItKsnkEOR9VrRLIOE8uWe/3e6Zaq3drnEoqtkD4GoEFAQhgJonDkFbFhD4FoEuPSAQGAaCwQMCTcsH7Qn4PFAIiA6CwQMCgeYRiJ33p6eBkxdKiTvt2ffSj1N35uN00T37+75FZH/GxDM1LGu3Ye3nA2JaGrjbPfvLyTQwtWefm5kGpvbsQxoIGqIM9+wTwD32tGcf00BQk+3Zx6QZQX+4Zx+TZlDas98y0ZS1crxnH01IA3HPfoNmYdGEpBl/MCB2fjryrYMYfJT/47Am/9bIlAWe42ng7E2mrd08t47dXIeX7JGXfdSRl31UX0fla/Syj6YtEqCXfQKWhTp42UdTtAlI9LLfo5d91Ohln4DuEIidN+MxUbEsMTE7QTMhYjQ1spyaGgmWcWrEKYg4NSIEbGqEgBABfzg1EtBMiFjAmRBjGedKTJwJEQdTIxEQR51L+7VFJLG7QJ6cBu7PFpHamblFZEpPPOiwXp7KxHaTBo79dNPe08BbJE3TojnobDQBjpqYAI8ATYBr2WgCHE3BpTMCmgBHMwxR89EEOJquwICYADmDFe1wGnNOQErs2e9224KmdLtKpguihW0ApsiALgDAzwUIJCAdHoFnIOBKBND0bQIygBKHpu2AtvkOACmDwPIQCCqALgHRbcfOUeqLbpuc4606/TgtHcC2yd1PgJ/WtYEHHdbsTQ+Tv+yP//5WYtNDohLHpnTnGhMffV5nd7OBiTTQnZwGTvvpprE0cPKe/Wq14isV0BBFsVGNLgFcmF/z0bRKBGglpYem2EE1+wAaLpq6juo2AdRNNFUR1etVcSUlmnKA6vRo4SSakoHqt5nz3W7J3d6e/tNNO3yKiipRittW+eB2Cs/8QrZIWNTkd1rT3Eh8xTAnN/kdf7op8UNX83/FeN9PkVM6lfw36Z+kNxioU3fp9BioUmElup/0b6hQ5+3S/bQwzjJhhe5nUGXntSnwoMVK6qkp59vfO/hNyg9/3TvuuuvuN9xzFxxvRLnnDXdPAm8aA28C8+4Y3DUAeN49b4xAqqQxcE8avONZn43C+syHP3gmHR/4n+2nf0v3/0VY/wsVcmPsnhBHDQAAAABJRU5ErkJggg==" alt="">

JSRioqSkpKYkpKeh4ePlpabhoaTkpKTg4OFhYWagoKahISag4OaiYmJlZWvjo6kjIyhioqgnZ28kZGinZ3cpaW6pKS0tLS0srKtu7u7trbTtrbSsrLSrq7St7fSrKzStbXSt7fMsrLMt7fDuLjQs7PJvLzKtbXLvr7WsLDSvr7eu7vhtbX/rq7/r6//pqb/ra3/qan/vb3/19fYw8PDxMTExcXExsbEwsLc1tbWzc3UxsbNyMjOy8vexsbTxsbLwMDOz8/YysrLzc3LyMjI3d3bzs7Lzc3O0tLR39//3d3/3t7/2tr/2Nj/2dn/19f/1dX/1tb/3Nz/29v/1NT72dn53d3439/61NT41dXq19f43t7q39/u0dH50NDq3Nz42dn02tr+zMz+zc3+yMj+y8v+ysr+29v+1tb+19f+0ND+1dX+09P+z8/+1NT+0tL+0dH+3t7+39/+zs7+3d3+2Nj+xcX+2dn+zMz/ysr/y8v/xsb//v7+9/f39vb29fX1+fn5+vr5/Pz75+f/+/v/4+P/9vb/7e3/5ub/9fX//Pz/5OT/8vL/7u7//f3/7+//8fH/5eX//v7/8PD/+Pj/4eH/8/P/6ur/6+v/+fn/4uL/7Oz/+vr/9PT/6Oj/6en/4OD/9/f/6en54+P+4+Pq8fHx6+vp8PDu7+/1/v796urq6enp4eH+4uL97e3q5OTy7Oz7/Pz88fH2///++/v78/Py4OD84OD75eX+5ub+5OT+4uL+4OD+////jSJMrgAAEQlJREFUeNrtnHucJEddwA9NYuIjOaJIICI5kmhUEi8qCZF4oLyiZ9DEF6iJMagBH0mQCCHhIZIL0ZnZ3eN24SICPnKXc3dv924hBvVAAXt6pmd6Zqd7Xt3TvdM9QwKREN+oEVl+v1/NdNVWP6ZndjdZPh/6j9+n7nvVs7/dqq7+VnX17Frfkceur6f19bS2L61P/kPU8Y+f+jQen6HwmaC47eCfhmn9wRk/uHfv3gsvh7D3IgwXfw/G773kYji+D8P3X0RFDi4MgQvjwSWJ4OIAXITg8u/4oUFab/lhLCh5jCqGQhGjxkGJgTJGHUOlSmCVg5oEDAImgjqBRoP+r47AxGLNCCqvEqgS+NXLB2m99UfoE5oYWxjaFp2AoE6gYhPoIHDoZ7gE1vAjo0GNfhMVQZ5AlX4TB3/XPP2uRUrcwcTXCLgEbnjRDk/rCmqADtXC0OVZsEZs8x/Kahj0Q818kGcINCgLFUGZ5cmywI5Qpg+tUqs6dZ5nY0Nad17Z6XZLmWoXjmwJgqWWhqCNoGTpBGoB8MwAVKKBQiDXAGDksKhpBAwADQYUjNlKAEwEzRuDtF5c831/yoTgT2Nwsv4QeDNYbOUk0GNASwAZjDMIFAIZBhQOegQ8CBqBHAL7164aNuKP8guP/t4lN2gR1ohd1kTlALArka6zGMCuRJ2uRJVfiWo9uDTZlUj/t6rzK/Gm+C5vR3f55mRdvpyyy0t9K5RWxdqytPLjpBV5Ja5JV6IpAJcD1mahViWgc2BUeSOy4ZS36qDNGkHlsgBu4l3e8DxrSvc9z5uG4LeyFgGPA4jWDAfQwxGY8G8lDOBsP8OABgA6NIKMALBGjsC0AsDkoBh0+TuvbBYKpV6jAEcWg22WhqCUw2II+AwYALoEPA1jhgNfIVAB0M5QDS8AFQHkugAMAooPsXBj7HDKurwpD6cCMPi1OrjOWCMKoBq0KmszNpwSKAuALs280IjpurwT3eVtuYe7wYUX7vIq7/Iq7/KDayC+y4+flrHFaenRt+p6fd3sQ4TxAIqQFkS9Cf9eZcAm0EHgYLFBQEVQJgBpSaBIYA0AZAFFyAJBHsAaAfjjQHTKAXAJBGm97SWuquoHMyoc78OQm9GHwDmEIDulIugFYDYE5iLBoRbE1iH4OHUuBGax3iEHQo8Dhd98xhcbgwOxEaOH0y3wLWfHpdXfaWmxcasZqYGOMG4JGujK1hejgeXJNfCtV651u4VeFQ0wWwAfs3WIBXI68sKCxUCjO6hR8M0AtAl4BEjy2jkCWgAqBBSFQIW8EIuahzHb3gg2aCDcl9gt8CAGJ+sFYBpDiwDd8Rjo5QKgRIMMA3QLZCBDZ7N7IhZzDLB7YgBCGrgmaaA2vgbqIQ2sb1oD+9IAYYZG+ZEzH3W7rsSnM63iiAnZoBG59cVooJ5PpYGrYiNyDRRm1eWoRhytgT3SwBCI0UBmfYIGTkdq4AAkaWCpVIIBAo4sBlvH2KtB6BKwTIwZAjkBNCC0CfgaASMAnkKggiCDRYWDCgHNI9CGYLAaBG6MHU6ZBmqh4ZRrYIW3KrvOxFl1Sg2sNlJpYF/yLTNh5hO6+STOfKJ9K+WEbHRane1Iq5yQVpQGmlwDjWgN1COtb0wNzKfWwKysgbMjNXAgeTEaqMoaqA6tj4EeF0Xl169KM5wmNuJol1+TGtFJaEQ2yt/8oqc5rerXZlpXSC7fFaavLT5uCV7Ixi1d1kA1cjWQ3XxCGjiYvq5KGnizoIGlUr9XK+AoDwEm+30CNMojsMxCAHIIfAKDQR0BWF8UyDEAH4caiIBGeaoxADTKUw3QwFKpE6+BrRgN1OM1MDO+BmbG1cBujAbm4zXQCIHo1UCda2CjEamB6UZ5J92yWy3lArg6UgNvjp2Q7ZC0BA1U+ZUoaqAdqYGC3BshwIVB1EBxNZC7PFOK4sZGBA30fdRAXAC3aAHcQkDr3Qislgx6OYwzCBQBTLH1bgIZqsFBhgONgR7GaSUAOQRVQQP7MFfr0eOCWQy2jrHH5okYLBNjhgOfgzYBj0CuwYEWAIOAohAwaFqIRc2jj2vT44IAJGhgd1INDK8G5qXRc7QGjn/zGamB6qa6fHGr7onp0kptp5tOq+FuWVrluLTiNLA3zmqgCPQJNXA2vQaONasWQDXa5Z30f63tTit5sv81l1ZIAy0+TAnjVuihsC4/FBZAjfVweTVQFVYD+ZWYV6PGrSvzhQJq4PCZj2v2EbBHPFi0ZWBpGDM0Icut4vxLodlViUAd51+sBj3zoVM8LwCVDAf0zIcBxYe4Fozyb2MaqEZp4GCtj2vgQPIIvP9nr7vuuuvf/0s/d931P/8BKF79e3ddjeC11wPQJQ3MCV44w4GggVnUQCudBjoJGnj4zB/bt++l97/upfte9trP7tu378fvuvsnEPwyggK3vm3QwKSnr488GnzwYKNJPfhNXv72yC6f9Chq1IQsbVr3v+JzsROyZ71j1D1xZFrR2zO0kQ+FD5/x+Y0aKKwGfuc7A1AXDWIcDaz4vj1lWgMNtJysTYD2KZAGouTZJHkCcP/0rA8WfU+u4c3A2bVnv74GYIaBQAPtwT4Ie6iB9mAfRAAkDWxnioEGWmobAe0amcWirxNg1heA7p9984dwkwgCz6Qaje4AlF75rhI+OWC7RvD/NA1j1uBAIcB2jQSge+NV42rgmqSB9+99LHY18MOfDcZXcTVQ3QYNlH3rkX/+QtTNh9I67x0pV2xS+ZYzTlqHn/P52Hsi6/JbkJa8pDtamg8/9/E0aSVL8xgaOKWnsT7zI2f9ubahBl8N9L7lN7w0D4UTNbCO+/WYQdRpOA1AHZ/31Ss2Rp2DhovxL874Yh3+OByw4RR7cf0PPxyAPNWoVgmwvxYWizWMg78WBzeP2HAwerL/xOs+Fevyv/mhzTbixGn9y9s/HZvWc9696bSu4NYnDhAhDexIGnj4jC9GaaBw8wntDRQ0sJhGA5utBkhYgYzNNZsIDK6B6HTNHgeWArHzgW99tDMAvkI1KlQDzl4774/WAMga2My0aS9QkwOmgQgUS9LAqqIoMyoE5SCG1qyyEfSyHExjyCDwPnLWB31FI5BjNXQIBOzzf8vGyuYQKLmcMgSmCDQIOoEsAmvU3sAkDWyzRnzuv67HrQb+278HwrAuWt9IDbxpxHbY0cPpI4/+R6xvveo9o0b5GN+6YdNp3f/qVBo4aVry3sBSjAYKjeiOo4GiQYzUQP5Q+JqKZblzpgXHNAY16yLQoOjP2JZlOzmI7hQHrQzEImqgCIQajWe/vgFgRgHgzcDH2b2ePQQKgUyLgL8R1AQNLLTbYH0QwPrgAA0cAnA6OMD64Mhx4BFADWwbBBRWowaBQPeV7+oOQYNqgAYiaCDIYdFUMGYNCDUCOoKQBnYiNVBN0sBLHhuChnytChqYvBq4HmhgsZH+SnQSfEv/z0/GLoCfN3LmM+F++cSlEeZbz4Ircd2jeWIFI5237mP4rnc+fWmd+St3/9c9txy49/HPveENB+790ntvefc9d3/hnjfed+/j/33mHwcZssRLJQ6UyFu1lNbkGvgDz3vJ/3z38y/Yc8tde86/4AV/+Qt7nveCF//vBedfsOeNv73nF2+97bbb3/T7t8Hxptuh+OY33x6AO8w0GviTdTjMPsYWBsMPwCoDNkadgIPFGgOobesaXSXUXRUO1r9x1zO+Ifp4xq5vw7PdKkZ6hN5ROUjnW2PtABdG+fXTXvhXDxw5+uADDzzw4NEjEI8dg0Dgr88+Z9MamJhWJymtS5+cX1g8Pj8/f3xxAeLSEgQC/3fO7jHSitZAcV+/oIH8rxXzUBjSeuT4/PKJ48ePn1ieh3jyJAQCX969O1ID5bRGaqAra6AfAqSBZH0lWtrrnHbpE0snlk8uLS2dXD4BcWUFAoH/3312PlID/dQaqDENFADXQBHIGqgUT7/so4srRxbxOLICYXkZAoGPPfPc2kYvFDTQH18DQ3sD5V1kggZCI355fmGZ+tYy9q2TJ7FvIXhy9zmRGlgzJvOt6Icrrcibz+i+NfCt9FdiUlosi6ckrbE00OGrgQIQHwrrw0Y8vjBIa2GYFoFBI9YaQeVy1JLunde0yfpAwixyOjUXaKA1jUUGphSSPCw6GQm0GPACYJx+2cdWTh5ZXFlZWTxyEuLyMgQCX9l9bhdq9FruUAO9KSz2HDdRA/2RGqhwEK2B7cJpl35laekhGiAegrC0uIgRwRO7z+5PooHtGA3kkmcUI4Hg8ol96xxJA8uCBt4w9hrEOI85xxrlk9bld3xa4aURvl0rdE9cFe+JE6aVj14NLEqviIgaiMWsDGZDYE4C9umX/c3y4pFlPI7AnWf5oYcgEPjoM8+tQo25WX2DBjIgayBJXr2HoeJz6yNgWBjVZuCFTAPZ+zMEqjKoJ/61uPW1SAOdNBqY+uaTsPUndSNuzc3nKU+LW183RgN5l2/IewNrMkiRVmOUBpb7/U7L6MORw1A0O0NQyDb7/aarQez0KghyCCwlACURtBFkEKwxDcSRfUnUwCXSQPiBTc/HUzJdOKWd6SCwAORFDdQ0bcaBoB3E0JvTNoLMLMZpNQA5DswQmMbiCA2EGtksnWJCUOmUbA5CSg2c9BWRiTVwM2sQaSZkE/rWDdud1pMLD6/MLywszK88DPHECQgEBhOykWklaWDoFZGQBoqNKBrECx8+9uDHjx47duzoxx/EiEUCf8umr4PlQVkDhdXAtm0X5zTXtu0ZCK6eKSJQ4N8WATXjbgQOgSkOWj0CHoIpBBWY7Mcdu769jae06BQLTvGm4AeiBtp2Q9TASqWSKUKozGLw1cpG4BHIEchiUHQCVQgGAU0G/t/9/alTp249CuHorRBO3XHHqSH4xCfwB5omfZwBoUqn6BqEtqyBa7IGrsWvBoY0sCFfq402RvogtuzV7/MVMC+yESfVwIQ1iAneT0y5PWNTGrh9aSU8IaskaGA9+iY58MKE1yZrggYKjZhKA1Vc/BM1UI3RwGgvJMljYI4BZ/hQeKiBEvBEDVxdXdVLEFZ7GCo+RrUAodzComER6AegZgcgLwCnGYCqS6ADYc3BYrEYgA4Bt4qxtQahScAmsAWb8EZv8Bzn9SN3q/YGPhVpRb8iIqe1Lt8T68I1IKwG1niXXxXTEh4KyxrohjSw2QTra8KRw1DUOggqUOxnsCiCHBZtBWOvDaBANSwvGnQBlHpY9H0CJQBdAh6BDII2AxZEUQOLgfUdIuvjGmiKGuhEWh+BbMgLswHQWQ0CB3UE0xJI0sCOtG40wSsi+jhfGJNSA/vSjGKCdzHUcb4jKaUGjr4Sn+K0Qm8KJ2lg9CsiDXkhSXzJVH43a1X+rpHoL4y5puu6xVnFhWOmCAE0cAjsKSwyMMeBw4AHwGKgh3HK56AlgRYDFgA/BjgQjd/hGlgCecu5KGRzEAzfMQig081i0VMloDCA1tcgoOmRIIughqpnmCaBmgRmG6SBWNQ1zGDUQ2EzQQMHr4gkvOcjNKL4ZF8PNeIoDZS7/FjfzJL41U0pvzAm3T1xh6QV+RUoyRqYsF9eeGS24UqM1kA1XgNJ8t6nyxqop9NA2fq2QgNRv/RCoIGGHwBmfY2QBlqSBhZlDSy6AegQcAm0Otz6irIGFqM0cIJ9EJ3NjPKjnuzv7LQ6UWnFdXk5z1qMBobSitwbGJnWW15Np/EJcL4tgQ4B+kFsotzpcsDmzARcXqNfkkChwKfZhEv9SPC7PzVI68A3Xb9///6fvnY/RgzXvmb/RvCaicH+VOBaDq5+/s8M0vrSnxy4b8ccB+57bJDWTjx2aFpfBce8dxlGrnk9AAAAAElFTkSuQmCC" alt="">
而这些几何运算则可以转换为一些基本的矩阵运算:

AWTdIxWYIzKGInK+IzQGI3SeIwqwDA4MRIdAB9ogS4tQAW8Mx3WsPMCORYMu9UnIxAj5SI7XHZmg1B3XtZNeeh0Efd+7tYmfacPYccEfSBYKgh9mvMhFKATATJ4VycJWjhJkJONm7J9iod9SAEM5BcQjXQ/ujcNw7gsNJYGdYeOMNOBC1SB7DCC2CV2YTIHIOkIPfICGSAbh8eSoUJytACDQvgcLzJ+kiF2bJEMDfQmejgIabEoc0gzSNB8RSB2yhBzCzILKuMkcJcBAgktLhiAZKgfOaQC+bcXdngG+pJ2ktMzMuCAJiQah0CFnDBBtdgiXnaVZqkVMsgJwf/HQlnJRvIoOvjCSuxYLGVAlCwXiJtgUeOTBJBXYHFZBmWnFvgSbbtDLchFlsU2lifJCS2QFVRyJ6lXXYOpbsXHf5cjMG/DhwUJbuLwARlQDMpRQwJ2mQT4kSABbPBQmOQnMCvEmAhlCY9ZCTkBWE1wfPmFmhs2l0XgRMxwLGAIfospkmPJl/NFTReCJ2+pXa0SQ+/WluBHTDZEAUEUlpqpH9RDPVoReosEnctylVvQB/xmnbU5X8XlE91AAsDYXVT0njTWD19ERszUMtjyAS+ElElpbfOJDtJpBAvXcOnQnKfwAfR3Tigmnk6Gi5uEnL0UmQTDLp+UHcHHFi3QKhf/p2P9aCcOmkof0hrBEJnCoJ+GMpq6hyGUF3dNJptowKLatBIOxBZjM0qrkpEltqFo16HShFSjiRqk5GSXIEutlKEnJqSv1B73BJbTAVGjBEg0qktC0Fq5g4GvYoAWBpTAVIHg+W61Mk+iCTkKwgHwFjmhRIr78CL78SYkYKDw8HLsFgsQ6jnDkQGBCQV+UFOKIStCdXjn+aaDQFVDsA5j9lA9aierxSR2NQSL5aeowB43xgx6MYtCaSkAAijlaDDex6inUBIk8C3WkxSzGFZNYBf4GSJl4T2aCpm88SHgkkgvMAwvgKqjBxvHYBJnmFhDwJ2p+gmi2RqiuZJP5EkDcZoGGpKBrxoM/HE2UPl9uwoKt1kuorgtlekLNeN+NvGZzSoHWJA1J3IaU4BB3xp87AlUPJKtn3BKR8Aw8qEhH+AkM+MFZHc6/2mugcBLcAU2JfV71EKk9DoL6PovwCKFe4Sb/eoSzgRde8Ibh5UFCYKt+gUbQfFglR/AVVb3sOtzSxS7W4c1MwRqsd9FJyTVpXLYnh67XZODWh1bspKgXB6hItwxEA6rsp+gm3WChD2BOPsCFKIns5QgptHRKkiwf7siBpQ1rTxrTm9SmB/ADHhBhzR3tOJAs1ukH0K3LzPKNtsHtbGAF4viKvvZDHXwtARVHQFDolq7CVpiHatkEl1BHbLTp2f7BxRrM9cGEIkHAIkjtp3BrHF7Cjq1J4UxQku6R0TbmEZgUnjbt6mAO66xQpg1tp0htYoLCrpnBjlGeJO7OTGbuSjHuSy0s557XkYbuvuzuaSbC5h7uqhruqo7C6nbuq7LurALC690O7u0K7u2mwq1m7u6i7u8+wl7FIl7ZKO/ewrVuDD0V7ziwGULs1zKWwsyoDAK+ry7wLyskrLUqwrRW6PZaxDMC7fduwk+Eb4V4SHke77om77qu77s277u+77wG78ZFKX8Kr+OwBZ94rv2Kwc5xJH7
iwpUMIo6/5sKxxB+A6wKL4S9B+wIJbnAqTCpDmwKXRrBFFzBFnzBGJzBGrzBHNzBHvzBIBzCIjzCJFzCJnzCKHScwiq8wizcwi78wjAcwzI8wzRcwzZ8wzicw5wbgjqcl6Nrw7s7w3rZw7WovzA8xEQMsILWtQD3QAC3LD9sTaDbBvVbv0W1ShanD5WjlWNkcRsXUEG8YDtxE9zQBOQysdaFo6Ono9E0xWvAG4Kbge2ZNPHDxv/+xKAtCr5tHMVt0FfjSjcUFD8GHF1qTHUD5cZpILVi6ry9+BQky1iuGQd4TE5hXBc/uivYMZXPsSwlEz+RDE0NZaRrGQXgYKSLU8giGA2iPK8dIsrZwcqdUMocNqGypMBnkEvwQBP40Zzxg8rrc44AZ7YA+sQGp0D4NoKxym/T+wTkyW8vVCHVeY4vtKXC3AZP2qY7cS5FYA5KED9zq02i2gbSM49iecwfSwlOMg0MoVPpDMV4u0KvgLje5EFmYDtMsKi/oUgx56INewifLLqhwLhgczB3GU3hzAbjbBU3BoJwrKs2QwZI7HV2/F9G7DXAEm9u+gePTDAlE8oe9gT/Ag1+h0DPZWDPWiFnTTCcusOEX1LRxmwaLu0So/ACwMY7r8GaJVIlNc1ZgHotCZMiuzLSVvwEYdUywzcldMJ3MS1z38XHS/FQZHgLjeBER8IeQqsWENYFFKUI4xJMhEDS7PM+TXDUsPnSi7HU1aHHfRSzW3xZtowI/bAZnToN1wke4BcDrpcplmElSFjM3UgEhAUbtNLIgwBBaZDQSzB8sUOK6MF8aF2zNqIGDPhBQ20Iogkbo3ALVukHhmN4GThMQQQM3MpZb7UoSdMIi8CbYZ0bpDLWTwAQXtadXPHYx9PUJ9Q9xIsIy7IeltcHDbgIiLImnn0zluUhTMNlAbnQ/4Rw0NHT2PZiC39zyo59nOcMVQ5r2G3QUIT0C08DDhpILQCxpsNdJUHz
AntaJUmzIqldCDViNo/shlpTHRPNKbNNP8uSofgcdbZNHw4L1i1aOhj0BKiDCaPQCkwyiriFFmwTKPhbLhTgSRriZSg9CKi6I1fdDNGLIEU93/MB0UGDFxsLBXSsfNXtb9ed24T0LehH1FgRQw6SfLr3I+yStLIjIdUBG3XgBao9BtKBxkOYQboS31O7h6H34fkIBZXDdPycdEZLeP4dDQsD3x3i1yVTGK1hQc+RtxPFDiDwUwlSCDjDFnkmqzujQ8003UvgSWOg5BweB7PCpclgnd9Jnf9PTG/AoEhbWud2jkPEBJ15rueA7m7W2TAODR6zdxs9ciWM3CMm7ZOKERKuJEX14VbBtyz+wnSTvLIWx0nnYJXz2Z9dHOqVY5WbLupZLKDn8CSn3g4Z1+oVZ+rejbwrDtiFPhbVoiHYpTKI7ZMGctPBRjV9h5/8yubfE7MARuZxAIOtklEjFOSRIR0OUM2YDGRiLQUTS6Dabdb38+Fvjelt7ggIRnjYjUmrIuVBGzIi5ErmUR5DILmLIMCqEFa/gAwkOuuCYUA8AmwvNVLG85PkCAzATidYCpFbwCW+rFXG3t+VvQUdk2e34FG5A1IoZp2YQIYTWwXoUhhX9eBHswpvTx4FjZ7l+9oEx4BTgFHf5mwaTT6tH48IExjUhmcFT/QOFOB6pEjGTENSb83eCy99Zj6UoxHRoKLU1A3TKHHitBsMVbFb0Z6Bon0FfpRTINJX19DT5IDikVIa+nIRoBLK66Ac/1zEjrnfl8XI+gjL/y4vMuWROLg1K3QtW67HnjQtKKkw7pPh3AjLi3NxebIVNERPzpHdxsuSFexCIUljjORoPdmRKX+zJPEeMMLmRxn6a2CQiOct31JQ8Zg39KEXKJUPBtg6jMMW+fhB9sc0gcWgjTOIFExCS0+RHfo+yKcwjMT4n7p3jCSuBPihhKLk91UnK3uQBSiuB8do9rKAyBadU/hBTezO14BgldW4tOe4DrFT9R+RKCDwlV6280sxcqjDD2G05N9UyWpAPUKFqEngIVB6qXHwUN0QE1OBn93wcJrgB5iQ18twD+BQSQefmUAAEA6JReMRmVQumU3nE8p0OKJVK7HSAVQoQq4y2/+qCEHUa1XFiXmFJM5HRu6MAR8QBwDSnvl9///rDypQsNDwEHHoo4PRoYOCosPRkZEuMarjo4iRaYSOY+RSdJS0FCzUFAs1lbVVcArWATIWds1VKGZEFwSAwhaABLLJdyjj9hg52YiQNaZLGTo6aUp6KCYDW8uTrIW3aVvIuHqcXLBilfW8fB3ZkbwCO4Oqg5ekpSiGJIni8579H+CSGC0kFWTEic+igws7qEAXECIiauPgZduiok6LERRGYByx5wi4GCAjlvzHQRKtKZr4qKRlyWTMPhMBPhxSgeUSGb9k9vT5E2g7kuxA5CTibQmHZ0GZNnX69AxNgDyjuIF6FWtNVqxStXb1+hVsQElhyZY1e9YUV7Rr2bZ1e8TdW7lz6YZVWxdvXr0m7+71+xdwsriBCRc2PKrvYcWLGUsZ2hhy5MiJJVe27HfwZc2b81KQ5vwZtN3HoUmX1urZdGrVMjOvdv2arxnYs2mza10bd+5jqHX39l3o9m/hw/3wJn4cOZLgyZk3L2LcefTfy6VXHw7devbVFbirUMGduz7t42mPiHc+A1Xy601fQ59hNHv5oM2ftzkfP2f38dTn93+5Pvj+G1A/bO4jEMHGzBMvwQYhG8nBCCWckMIKLbwQwww1TdyQww49/BDEEEUckcQSTTwRxRRVJIeDDPAYaMUY/6FAk7FkvHEcEOJ4Acceq3khGB+FVEaFboY88pZrkFySlUWYfHKUDlrAA8oqmQsCADs=" alt="">
这几个变换都是线性的,但平移运算不是线性的,不能通过2*2矩阵运算完成。若要将点 (2, 1)在 x 方向将其平移 3 个单位,在 y 方向将其平移 4 个单位。 可通过先使用
矩阵乘法再使用矩阵
加法来完成此操作。

DSTgz5Jn6VrqVxZA5uwkhR0x7reQp3qUiFZZpsgxZ0FFgDVERygSzFLXWlHttQllSA/FjXBajOqB///IFS2ItAhfBYQAbrSFm3BoY5f0Oo/AKgnrTT77dcQwEN33SsCNM3tz3yrXEZQQDJQSs1pfQbZ6urhr1ri7mW9uwfTmEwH0JUXeRlhnFr8cwRFFMRI12uINBGFXPwrJQCgG0368sEC9EBr0Pa6VCANdQrnmYR/CVHWEVxXAehMzM/4uWAgNG1nYEIfbSZcYTQ4lYiPvYxxOGYLDu80eypAMSo6vAL1UGJQxmKHAPzTwcKy0BcBiMiNF4AhlkykNSxewfyMq4AFJEsCPO6tAiaQUhujAH4By4bA2DQB4YxAl0FmTSt9FoYu9xaDWPiGAP6wM0WAt8KwWGp32UOUS7L/ZCUBXe+0HKyb9+pCIOmdjKKy/Fq8ImcL/mgNwXIRZ+/OYrAh1UEkNcSchERmBGvkMwnM++ct1EUCljPPWBPopDJKGhw/80yi03Md9SKImGA0QYQ/CUJKZGYFQFtM1mKJVKIJpEVZW4MzX+UZwEmPAstRFXsYgoA4ToCksV5jK1oxm/0dYdlJ6IwToJ0Er1UXAaZ+Dp4QiCiZJSrWAFqzbQrNTQ3vmaepQWCkIXIzLMzCu3hqFwWek5o4b3qo4oYLubP5jWBUAGQq0JEzA3pX6Jz5O/uuZrxxc+ykYc1nrHKrgBIuTYCZIBypBcAEDvACTiQTBwJu7lBHvWHvLvIELpIh3wiUFRkv3I8cQMOmxHFCcWmKC8x0mAF0gebbg8+j5s9cMWs8Y6K7Em1XMx//96e54YSgDcvOOThAcpceBIdMG99Ub5t+J5b1s8Gx0l1nr2Q4S1VsVobCYd8n2K3QorQHwalBIflSgJ52GK+9Cm13+w+eKuosvFvvPTiVUN1N966HCSVynzjgeYAA6p6XC4VfulPbCXUc/H3xMxB0ubKQdz1cVwSImyIP1n2ChifvOTrweclVveotoB7TmPa1lqL1I+WluR/5Vogi0Tr1MXDCDThXAS5bVLmPyYxJxe988O4629COAQIh770WJEIJKCMgAnYAtptY9SA92WZ4RWy+KXOv6pBzmQ2jkXo2oEgC4nyUTRfoMiYEgJ8jUIH8qFOP0cg+VbPrANdelVWz/0IJ1xVFSiUzD6E4BxZEKfREruAOiccGL/VGYwY3TRMW/ENJfRGBqiYGOhI0svcDi0RTY9ZjkPYMBHZH9vES9LcN3cCBZ3BXqaJTC0ByWHYC3JYgFyBYP9BgP9B5PfQzIegDFhIOB2Fk2xEcJyEUepIORXB/b+MFHBE/lbElMcQlItBBvqBHnTFaEBYESadvzIFWQ8h46uBSYXAo8CVyk6YS8IVdNAODZYBknCB12tE+V0YFwCYS5nY0bIIJ6sGDRSGHI3B5JABCbHCDJOhmk+ZNkCQZLWIHr3ZHKfg1p6UjBBgIhLEQyTR1OtVlQlIM06ZEkoEA45UynBd53MACV/8yGgSTYwoBIm70NjiULKRxiIjFKsHBgELiCvNRBxkCaIR4NKpoIJNVOo/0by2ggCdodhDADgVRDJagBvQHaPgXXs+EQLfwaLPUX+3nKwXhCphmBA1Uhjw1jBZUjHkgfnWzC0djZFe0ErOhKoVSg5AmEGlRjVoQhnKhjljgQYh1BO7SdDKwcZ5zWiOiQ86xErAYRvmBevCiU/CRJ2Szj+iofDT0FAJAJQDQeAVwVlCzOLMIAE2VA60IItQgCl/Aj4Xoj9zwENWociWyRgdgD6YGbC4JPKqXAvpgNhNgAVRoejOzg6hxQtiEfTn5Oyz5Nm6kJ5ihEDzkHESwKw3hL6r/JQf81zX+JziNEhmUE0Vdoh5spEOq8G8TaZWL8xxGEEPS4Cx7FDCOtxfXeDZBNGPwE0QTRI0hZFyEAUCzYEeco1gjICuu0BrVJibJZHxnsJOmIn2DQIUkgEiIcENs9B5JGQdAZkGLUVTF0CgHoH0kYJYqxI5YkYpto49w8QfzJiKXGQcI5IugMC1MFpHUIBkmWAaVVwmtWQWeBjanUpGmwwnFoF6UMxo8NnVItpWdcI0YyQgliQKtdDrKEghTsCdesBB7NBgfaQRD1UNOBih+t5vLUwMNhA11SQkqoQYAxgSjJRtXZo6o+I/i+TxZERHbEACw8pPtdxI5SAa5+XOvbnWKbDJA28GCBvkqwnEj43KNgmEpi8Fb4zEtXoBt3wOaamZBTNY03MMGjDklYkBU16MmMxIfaYKeFbomAooGS1l6R7MGMnlHa1CTxoV2C/afJeYza1CJOUELSRCju+Z2SwmAryQQRPWjqfAQJcpa+l2XlVmjnHOHo9oxmN7YFH/waDZaYVeaBhz2SPdhpPwCL0wwZYvng1YQSSqhLDvkXmFSbJQgAaaWdivaBoYxZp/ACVCmENgmHymaZR16CE8WFI5JdXE6VHtqWoUaZFmKeW8wqIqqBX3aqGbAqJBqL5PqdXNZqZSKqYwgqZoKBI/aqVnAqaC6gaNaCKJaqv2AjqhamquKFq1qMK+aB4kaq2B4qbT6G6p6q/Gpq2/wqbyKe7+6qLkarF5CrBVjrAuKrGbgq8parM2aBeaXVM9qBUU0YNN6BdEaqNc6JUBTidv6A9H3rVZgdN4qrj5QZdpqroUxn8ZKo+r6rvBBGq/yOq/0Wq/2eq/4mq/yCpSf5K7mekK5NazKKqIF0Hr6Kj5oqa+XYUhOqq975K/vWkQKWzYTmwK9daj0OpLfFAIAOw==" alt="">
综合这几种基本运算,数学家们将其统一为一个3*3矩阵,存储形式如下:

由于表示仿射变换的矩阵的第三列总是(0,0,1),在存储矩阵的时候,大多只存成一个2*3的数组。
三.从由4个新顶点组成的图片中找到对应图形变换的规律
方法1.通过矩阵乘法计算
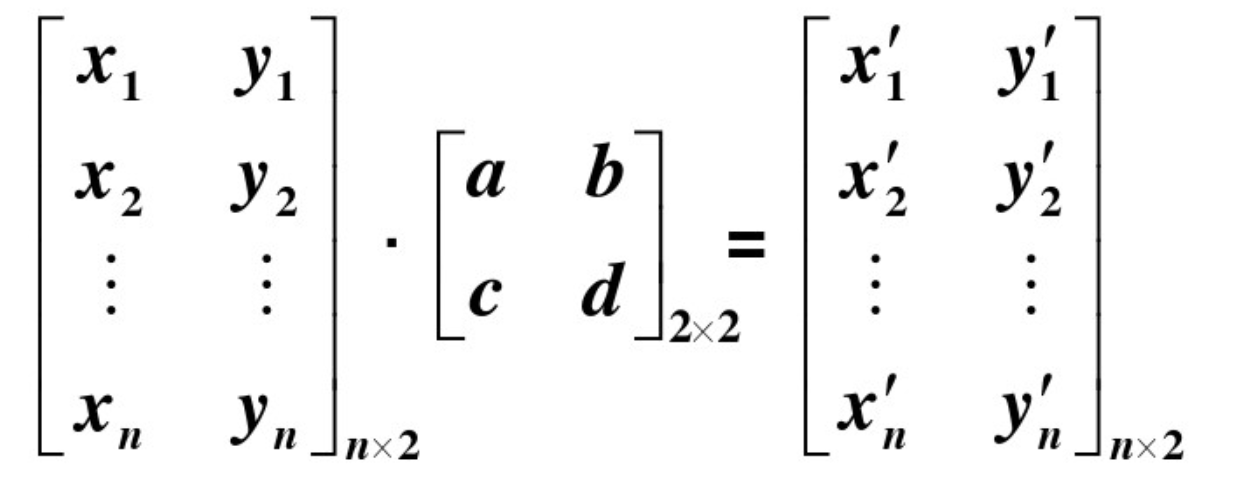
原始坐标和变换好后的四个顶点坐标我们都是已知的,可以通过已知数据建立一个4元一次方程式,得出a b c d四个位置数然后计算出新的图形坐标。此方式适用于做数学应用题。
方法2.通过x y的线性变换找出规律
我们之前拿到的图片都是很规规矩矩的,是一个矩形。加入得到x相对于自己图形空间的坐标的话,这个x的坐标就是 (7/11 * 图片宽度,4/8 *图片高度)

SSDZIQgiEwdhgI4E+4xDb7QBx222nSdKdjjM06eTrJF8cnHQ7PThObCefu23HoQ12bCwbAjaDQQjNQoCE5gmpSjXXG+90pv7tve9Ude8tvVvvnqr73lu7bp137rnn7L32f6291l5rD8f5r3/6Z0qpxFGZo4+p+XDl0Ucffe7ZZ3/yJ3/y1NHjvnJmylOOw29p6jr8ml+ChoHp2LFjV
1999Sc/+cmpqan3v//9x48fT5IkDMPAcQfeP66LTtbNCYhI9hhlaaPRcHxv165df/rZP1tdXf3pn/7pJ598cv/87u4DOZzFTmBJ8jRhmhY3SzlLnMhx3VQlS9XV2Ennd+/6/U9/6oqDB2+56k05UHH+Wd7z9Deff/bZn/qJnzx17LifubPlKVd5WaI8pCtzU8PNlHMjkxz9LDr/wtbx5EununL1gdu1XGVxUiyELkkpC3W/DKwj4/O8xcqV52m5+rM/68rV7t2D5cqIwXmWtZ7H3DQDiVhlK2urHBd27/r/Pv2pgwcPvvGNb7Qt1Uvhn0LySCA2rP2up6z13GPrK/pqGFb9srpJ9ZWPfqeS/Zx+5ZVXVlZWEEosAdJQDItYpSxJalFzGChjuT5Msufn5zGNp0+fjqIISsrlMpRzJWnmq7mGcdovBKgPLBPEQBWWCWIg0uI5FigGZpI4bouktmXKjGXyi74LPV4QO1niam0C+2BicuX1A/O5WBfPkKvUQa4wS6mTxc2moiambr2WidrkSmq/XGGZXOUgZgBsoe6XgfxIsnKFaK1Xrnp6TnlQVQgKEON7mJ6MttmRq2uuucZaJoVNypSRQf7mbpl0GaKvhnO6X1atZdp0+sq//Y47dDXpsMJvpcXM9H7UE088sTA/f+uttzpxSr8pROXFMT5ToVwaDssYfhmmh5JU26EvfOELlUrlxhtvDIKApgtJM+XKGEo9Rxa9Ld+0RXthubbm+77yXFTYvffft7a2dvNNN9NCy8o7R2Yb/ynWvNKp21k2BNUba/hMXuDWkyj1cD/cr339rkKxeIfl78YLHlMODzz/nZ3I1dtvdXC/E1X0AujF+hRLJS2CFmFztJLgj6ncYdlUtS51vnBVV64UohbFlXJF+0z2sT4ZGJbbxq8vV7VcYQCQq/vuM3J1881ZlnnuYLkafHXjdLRzaFZrEOMEfjOOdLzEc7/69buKyNVtd7TkEFEEqA5ELcjaz4/9ry1I9NUwYDuM4AbDC3th0+krP420z9HvMxGqoq8UOIEXtCSPvhN30mCGYTKW68N8psAPyJ9GAlU0DNeEfcJCmDc93SbXjuPZPkilpC0iVtwLociDMFcHM3LHpxPNS7XEdaN5WrPrzmtadL2E7i2EeR5MzBsfCh0pQZKPXKnAI4rnOoiUHwY6jodcDYrmZTlH87ygR67CIkyEkU4QRnF0UaJ5WESLp5YqK1eIuqOgZyDORgwG/jKeiwUjVxBQ9JArI/BWrrLI2qA0VdBw0aN5oq8sv7eMvvJd2zJNH4Sm2PGZlpeXUbdRRuhMNZqRr1xcloLv46yMR+SH5KK1+6BUrVUhoFrVx6WlJaJ5tFv6ksWc6bHRgxZFPX0QXBMoidIEknCYONaiGvTsKJQHkT+2a5BgNYLxmSxBusdAPz+KY8aZIpW6oY8SgYNxmubNr1ErBlV4BJGKkLRGIw6wBMoLvIKWQxScrZA5WknwVb7ydrrZI1fLWq4CvJM0oyekLZOtXl8/dNRar//+eqzliphwV67qWq7KpcFypXmfa4oTIhOMMCVZ6hYCxqHhIOEK+qwWHPqr0NBRiDkPQ+vOF4lS+Cv6agDn+2TVXth0+sqPGw2q1+8zLSwsZEb+kDy35LvWU9DaRN+fXxrmMxUKBd/zZ2dnGfeanp7m3NKQNz2dJkdxFgN7DAohV1zX96a9ubk5IjCloBQr4MwXn47PZCxT12fyS9p5w2fyTcyfRgtW0Jc3PaNKAnJFTFj7TKAXBkyuYfACb0nL4SCfKcnZZyqEBV/1yJXja4Pk0htr6BPTrPtlYNRar//+INRyhXjT8WrJVbGEdYCegZl0g7oDf97wRcISkOIz+UnLlUN/ArnCr2wkjZZlmowZEKKvLKv7ZXWT6ivfty2hL25LP4nOEp4649KZnp/jY6icLGM63Ial/VwZ2NGF/juIZhD/r9VqtFgiVNYypVmaNz3DfCbtmrTDd1BFSlQCVHnTo/unBp2uSsp0vxmfCSWPSk2yRE+wVE6z2XQ1e/PlVz+nzn0FuWJ4UMuVFizlOz4dcHwULYeYAVM325asJPgqX/qJCiROj1xhpwATuWJ6Xhvqfhk4dx038itz82ykGiFvyVVq5Mr0hPpz1rzPNcWJ7jx4Lm4clGWOliv6YaEXDvSZsGH5JtNXoBT+2ugikkQSfdWC3eDTOretyXzZdPrKpwML5egy1IHRaFpn2KQ1B8MVDrZAO9F6UjKDAdyUZxqWPdEV5hfQXGkheijAJGM0O/TmQtawPgjEWDUKMZAEYRgqsNJ6Ns/EvOrejjzMsF9RpkRatc/kEMqje5ta9uVNz3nUtSVXDISZ2eEASC+IYDE+k7VJVgZaRzvr6zyKWd8jgTtErkw76IXa5mcpXF/e53PXALlibNX14O/A7Hrlc+ANG73IRBUTMKcviCVgElRLrtqKwEqgHWfifFj73SgZ7eddo3kpRfRVG5Iz/vbKg5XV1nGz6SvGj7SWt3HbM8ytoy2SdQtoLcxf0rcho/pvjqmXht5icJhon4ya0DCI7PETXpQdDOi9bfznPQQZRao7aySMdZREjOUX/AIkQRgQ4TaFQ+ZQjYsw3ZE3LLBNVGdrCGLA0BahVRucwkxqzU93omXF7a8X/QhJvXJl3RJsqiYMW2+rZo4WZ+tA5Ec2LGOgpCVXvpGrJCowRUNj2KKnxXJDhKUwP3q0XBnBRsi7cmWEf2ChuY/r6OE2nYxc4ZO35ao1JqhRggZ+sCl3eoxYiL5qwd3/xzYbc31T66u2QPXXUK4IAoKAICAICAIXAwGxTBcDdSlTEBAEBAFBYDgCYpmGYyO/CAKCgCAgCFwMBMQyXQzUpUxBQBAQBASB4QiIZRqOjfwiCAgCgoAgcDEQEMt0MVCXMgUBQUAQEASGIyCWaTg28osgIAgIAoLAxUAg762cL0adxltmz/qAVsatFV2sfOTD3t8sw2H/BTbc5MNixNxX5Y+3fts+N7jGjhlwEMbZndx71rRa7vfKQIv72x42AWAyEeiVVUvh5tRX4jNNpnwJVYKAICAIbF8ExDJtX95LzQUBQUAQmEwExDJNJl+EKkFAEBAEti8CYpm2L++l5oKAICAITCYCYpkmky9ClSAgCAgC2xcBsUzbl/dSc0FAEBAEJhMBsUyTyRehShAQBASB7YuAWKbty3upuSAgCAgCk4mAWKbJ5ItQJQgIAoLA9kVALNP25b3UXBAQBASByURALNNk8kWoEgQEAUFg+yIglmn78l5qLggIAoLAZCIglmky+SJUCQKCgCCwfREQy7R9eS81FwQEAUFgMhEQyzSZfBGqBAFBQBDYvgiIZdq+vJeaCwKCgCAwmQiIZZpMvghVgoAgIAhsXwTEMm1f3kvNBQFBQBCYTATEMk0mX4QqQUAQEAS2LwJimbYv76XmgoAgIAhMJgJimSaTL0KVICAICALbFwGxTNuX91JzQUAQEAQmEwGxTJPJF6FKEBAEBIHti4BYpu3Le6m5ICAICAKTiYBYpsnki1AlCAgCgsD2RUAs0/blvdRcEBAEBIHJREAs02TyRagSBAQBQWD7IiCWafvyXmouCAgCgsBkIiCWaTL5IlQJAoKAILB9ERDLtH15LzUXBAQBQWAyERDLNJl8EaoEAUFAENi+CPgqy6g9/zPHHM05VxYXF8ulkgUmjmMVp77vu56XmfvzAwwyBibP9ZI0gRIIqFarlXIl8APuzJueXnI0Um18lHIDL0yVqtbXstSPIydRrqeCvOnJHMMnXXFNjCbPkqVUkiRR0sx813V9LoPV2spK3vRoIkZJyFWlI1dpnMRp4BU819X1afO+hbOBPm/6PaeYqAT2ZQW/Wm9WipXA0+hBTRtXA3K7jt2r7Stj/us4VrARcuoOExF7hB96BhaUNz0OtU+SRhI7MMm0OEhaQa7a9EAWH6dNXfvvQGLHcNEWpAsVfTUIzi2jr3yFpkOwTIU42A9XLr300ka9zkmS0TBcP9RmgOTYW+2XHI6GkAH5RnFEi921a1elUgnDkOYKJTYNuDufS71VN5orS1QGMVBVLpc95UVZFDotoPIhwTCozayzivA8NFjYRJGoRCkPkubm54HorNsu7lfkqmnlSmm5KhQCR2GWekTwjNPc5Q2WBU6PXGnoHFc3CA1cP3j9V8aLp5Yrk7py5XpW+AcWlDc9mjWeF/penCaoAsfRcjWPXLWx0ShBWVvKcqfHoGBLsUXbkkVf9YtHLy82nb7yP3vnnVQpoQNC38hRqflw5ejRo4defvkrd32lurSC+SoFYaPRQKf4xbAfgjFegYaBiZ7a3r17H374YRrGwYMH6VFyG25c2owG3j+ui53OIBnaPr09uoUAkoALeh566CHoueeBe1555ZWK0j3u/FLsBJYketGWIjfDc1O1aC0sFgvFoBo1Yictz0w/9thj+y677E7D3/zoGTVn5OowcnX3V6rLK37mloOwWY8atWYpDFXmphgFhRBqIbCS4Gf58ndNdeXqtVdquXIzhdsURRGkWKj7ZWDUWq//fitX3N+Vq3u1XCHqAzMxYjDwl/FcjOuNYrFIq683G7HKKkauLkOuPnenbaleqqDB1TJIF6PFtfGUPSgXW1/RV4Ow0df6ZXWT6isd+qE+UG8/HaeJLluBDm0Q6J54Rgeplez9w3DZ+HWLY38+kGEp4ASqoC1NU02Mob///nFdGcpp/EiUhedaiDq0uZnGM7/kOq4lCaa0LZMurc0fB0w817EQwcS8+TVqTc+QK0xQO2k6gc5YJtsdb7WonPH0nLPlSiUpIOvUbuf9MjBqrdd/P8XqsLnbJ1dD5NyIwfqzH/nONn+MXDmqV66sZQIlaLBCz3FY+x254CEP2PpaZaXLsh+lzpAr0VcGPcsLe7RytYn0lf++226jFvT9qYD2mTg3tXryyScPHDhwww03qCgJHLdSLFtRSU0P3Z7ncRzmM62trdGLvOaaa2ZmZm655RYaDJaJkZVyIV8frl8rWU5Xmw1sJJwm9PLtR7+zvLx80403VWvV+bCSByydPOO2ZbKdR90wtYnCf9R8y1S60qhGhKR870tf+XKpUrnN8NfcMRGHB194tCVXcRIobzosm2ieq9IUy2SxRRpJbZ/JymNexJ9qrJVLZ8gVlonxL23U29j2y0Be1DB
saeQKPYJcfec7Rq5uuglPjiD2wELz9pkw0rpcR63VqlGWOr73xa98GWJu+9HbDJeUR7Sv7TNxxfJuIKljuWgtk+irYWD2y+om1Ve+9Tnc9nBip8KnT59GzsIg9ANtBDrXaTOd8zxOrJrtz5nGQFvFPtmwhs8wtadSX3dv+28e55Uegmzc1l4wmkvHMBioQHFAGIVWShWcuHGW3pcXuVsyup3lHgq5XXcelUPgpdls1pvNvPnVR+CrXECuqEKoRy6oRw/p2mdqV83oPPtb3vyFZYTgu3Ll+EwfyTzjNrWh7iXTgv8qldzAz1qujEgzttSVq0plGA603HxTm0VarlyXgVXkioSc25LhJmedVnhh6KEU6GqTpgEQfdUSgx5QNrW+8pn9Q5X647a47YzFWvnT3omZJqTVYjA43t3CZcN/hvlMaFg99yyK9HBXs9mZmMfsrg2Xea4MhvVBMt0c9YMQA0kQxqQMtBqDT+fKbsO/xY5vSbKTsiDBjjM10zoy6QUM1WQEhIiLYcKZyJc3PaNWCLlyunKVMNUyiTTJBUKj3XEmnWtLErJ88VS+C+O6clVsTfiM01hLu2nn/TIwaq3Xf/8AuUoSWDlMzvOem5dFGn9avXZpiRMbuSJiwWxda5mIoUDDRR9nEn1lZaxfVq3PNECuJltf+SgwquSbPgiihhNg/SMsQYy2ZQIV6g6/KVOeHYO18rj+pjbinefIvhAUSqUS47E6jGYSc9FoK/mmnj6INUX2AlO4bIIYSMIAFNwCVxgjaP+S118LUTeMY0ZiQrdIeUTz+JWOLYyjP8GInHUx8yJl9Hx1D6MjV0y8V0w3MCNMhnrP1M32u201/ZxnlMBHGNcvV5CjLZOtYJ8MjF7v9T4xQK4CLVfaKAxKrZYw6KfxXDNz6AECDKDNyhVmAL5YcKALGjo+U+vqeMoelIvhheirQdCYa32yai8MkKvJ1leDxZ0qokFQapglzgl3DAXiQv1Ax5ai0Lb4KAQWOCfccaEKH1xOlGgCCHhCEoRxbqZrD775gl21zIJxsA8mXrBy11nQxMmV1rdtuQqMXBm2rrM6edxmBRsh78qVEf48ylp/niJX68eKO0VfrROuYXI1cZprnfWR2wQBQUAQEAS2KgJimbYqZ6VegoAgIAhsVgTEMm1WzgndgoAgIAhsVQTEMm1Vzkq9BAFBQBDYrAiIZdqsnBO6BQFBQBDYqgiIZdqqnJV6CQKCgCCwWREQy7RZOSd0CwKCgCCwVRHId0OHrYBa/1Ku1vJLuyiZFfJsqhPpj+LD4pjc1z5uBVQnqA5wLTUchHFwE+7ateaGRMv9XhlocX+CKiCkCAJdBHpl1V7dnPpKfKYuT+VMEBAEBAFBYBIQEMs0CVwQGgQBQUAQEAS6CIhl6mIhZ4KAICAICAKTgIBYpknggtAgCAgCgoAg0EVALFMXCzkTBAQBQUAQmAQExDJNAheEBkFAEBAEBIEuAmKZuljImSAgCAgCgsAkICCWaRK4IDQIAoKAICAIdBEQy9TFQs4EAUFAEBAEJgEBsUyTwAWhQRAQBAQBQaCLgFimLhZyJggIAoKAIDAJCIhlmgQuCA2CgCAgCAgCXQTEMnWxkDNBQBAQBASBSUBALNMkcEFoEAQEAUFAEOgiIJapi4WcCQKCgCAgCEwCAmKZJoELQoMgIAgIAoJAFwGxTF0s5EwQEAQEAUFgEhAQyzQJXBAaBAFBQBAQBLoIiGXqYiFngoAgIAgIApOAgFimSeCC0CAICAKCgCDQRUAsUxcLORMEBAFBQBCYBATEMk0CF4QGQUAQEAQEgS4CYpm6WMiZICAICAKCwCQgIJZpErggNAgCgoAgIAh0ERDL1MVCzgQBQUAQEAQmAQGxTJPABaFBEBAEBAFBoIuAWKYuFnImCAgCgoAgMAkIiGWaBC4IDYKAICAICAJdBMQydbGQM0FAEBAEBIFJQEAs0yRwQWgQBAQBQUAQ6CIglqmLhZwJAoKAICAITAICQy1TmqZxHCcqgUqHfxc7ea4HCa7rFgqFRqPBeeAHF4Ioqn7Wp1WqG3ihUn4jSgpBxXU4DzxVvBAknbMMyywYB/tg4jnvvQg/TpxcaZYFsA8mwkoYatjaRuYs1l+QdmAFGyFH1BF4SLHC36bp4vwVuRoJd9FX64RrmFz5WRyTReKozNHH1Hy4ggahVXhK24MojrzMQdPRSpzAX2eR53cbNAxMEAMBtVrN9/0k0faSlKRJlmb2PKej05M9EJHsMXUdz9HgQEy9XoewZtr0XR9zkBMlNtvY8S1JmSEMitxMl9hM61zwAjd2Mtf1YRyIWTOQKz2jZn6GXKVRljlJlEJywfdV5qaOVsQIIaklCZmWz/xS6rtx2iNXprej5SrLtLRbkPtkIEd6kCvTCevKVdRE5sFtYKFWDAb+NJaLWaTxp9WnsAer3ZErFduWivRBg2uoA7Fh7XcsxJCJZ3hBKaKvBkK6ZfSV76AR6CjCaeMbIGC2BURRhOSlKnWVo02U43nmzrzdJyvu/aCnWep5XhAEYRjSl7Q3OA7ka/OQY+rRSrbu9kLUwklBDCRhnKxCQYnkSIzJ2kJkm6i+oFWoCl3trmX0KFSSKa0utM8EZ/OnR9Ow7oRcQW5HrnyMqefaKkC9Z+rmmqOtpq/yxRM+wrh+ueKitky2Xn0ysO7qjnxjZPoZPNaVK09LuO8NxiFn6ccUmHIdFWOt23Kl6dE6QydgggbTo9BfW1f1aT7J8EL01VBw+2R1k+orX6sy00ulD6IdprZl2rFjR3VtrRE1CHEEjusXyxaLYX23oUiN+IPtL/c/tLa2Vi6XK5UKR36NEx2qol/pFQij5ZiG9UEazQaWUrdLpSAJM8DJWm0tDCs5UqM55fZ25NEOLQo1IToRBYqIwfoeqq1UqeTNL1vo+o/IVQ25ShqNOAkU3GvJlZbDzG35o0bnWUmgR7L+zM/jzrXGWrnUI1e4aAmB7ITeBrn1Qm0ztxSeR0HrfMTKFX1B7u/K1doakj8wh175HHjDBi+6bZuj5SpLHSNXEEPfwlomK4HWZ+J8WPvdIBmdx12jaClF9FUHk96TXnmwsmqPm05f+f/1c5+jYv3e8crKyssvvfTQQw+tnl6ie1709ehOs14PSvkOpQyLBmCE9uzZ8/jjj09NTd1zzz1Ez9C5OmDVjHoZM/bzYZx2C4FW+p5bKpUee+yx1dXVBx584OjRo+Us315s7ASWJOMzaamz0bxqczUsFgvFoBY3Ezebmpt98cUXL92//3OGv2OH5bwzRK4OWblaXPJSp+QXmvWoUWuWi0UsUzuap5WelQQ/y5e/VedsucIyeY5rfTsLdb8MnHf1X/VBK1cIdleuHtBypbtBg1LXdR7068avRbV6sVj0i2EjasKRaSNX+5Grz39OMwmfiUYwAdE80VeW1/2yai3TptNXrfh1tw/SHmfSdqjZpH1iEhikIuxuU9598GF9LsiwBHACVdAGJ84Rf7d82vhxGKfp4+twGc6JGffq0Ja2I0AbL3pgDqnDqIz+xRyN1BmvosWeLINBDL5ZiGBi3vwaSOQ5Lp4hVzhJ7aTpJBZptF3q6D+t85x9JqaKdHhnQaNX7nitdtEDdatOtp2fo4Ib/cnIFZmcJVcErgfm3CufA2/Y4MU2f4xcqaxXrixBDhKPQLY922Htd4NkdB639aUUGMHRfvj1DLkSfWXwsrLaktjNpq/82++4Q9fCjDMxr6ATzXvuuefmZmd/8B0/qLKEPpFvRvvtnabWeR1acxv6smcWBnOW7r33XiIJ73znO2moNvk5WwI9/tZJpi3aC7Ee980Sjln2zHPPEmy85aZboiyacvKdMUjQ0GqEbmfZEmTiKej2JnMyNNHevfffVygW77D87VThYp9869CTO5Crt/8gTpGnnIIeWuqOM9m62bZkJWHw6Mr4arGaRYET3PvmrlxBFWOr9MYuyjiTlqt2evZZI1dvvcUK/8BKD/akBt56fhetdJlxJt1Fdbx77r8PL+qO2+5oySGi1g576hLs1fMraz1Ptenhr+irAYBZfOwPhhf2wqbTV0yI0pTzH3Wgj+bDlUOHDpVLJU6Y+5AmUTOO6cS5nkersbXO6diy8H25Y5aYMXX8+PFqtUr/qFJuhd3zpqe3T2prbinUjdS0QgYqoArLRO8bHZc3PRnFGjosH7TstRmivcmkmcEl16fRAtTxkyfzpqePUa9yAbmqWLkiDpTGjTgOvALzCI2hb2m1Xpzzph+WwbiuXBUr1iDR7dBkGFL6ZeBVKrmBn21/C8laq7blKk0QfugZmGvOzRFCmLObNJJYTxn0A3quyNVJ5KpND2Tx6UA0mMqBpJ/XRVuQLlT01SAAO4zgR8uLTaqvcDm0OjAHrWjthytzc3NMMLB1NzappTVoOfZiTsdhuWOWdNPwfQiwkyBsRzJvenqreVbVoyRitmC5WIYGCGM6BDqOTmXvI2M/1wwyGPUDxVCE64V0jmxkBZJg4oXEZz2VhaSsI1eu7xeoDWbpjFr1VjBv+mEZjGvJlZnmA1sLXmB6Hi2oe+t1lgz0/jSucyvYCHlLrlzPCv/A/HOnB9Z4XugznHSmXLWx0QIJZW1xzJ0eg0JHQlqli74aJBxn8WJz6av2jK5BFZNrgoAgIAgIAoLAhUdALNOFx1xKFAQEAUFAEDgXAmKZzoWO/CYICAKCgCBw4REQy3ThMZcSBQFBQBAQBM6FgFimc6EjvwkCgoAgIAhceATEMl14zKVEQUAQEAQEgXMhIJbpXOjIb4KAICAICAIXHoG8l9hf+BqNu0S7XK0319bSDbtdBnsysJtNpD+KDyvA8l3P1EuInI8DAbjGBjtwEMbZHTbsejCTd2uxYk857YU7PZfkVBCYGAS2ir4Sn2liREoIEQQEAUFAEDAIiGUSQRAEBAFBQBCYLATEMk0WP4QaQUAQEAQEAbFMIgOCgCAgCAgCk4WAWKbJ4odQIwgIAoKAICCWSWRAEBAEBAFBYLIQEMs0WfwQagQBQUAQEATEMokMCAKCgCAgCEwWAmKZJosfQo0gIAgIAoKAWCaRAUFAEBAEBIHJQkAs02TxQ6gRBAQBQUAQEMskMiAICAKCgCAwWQiIZZosfgg1goAgIAgIAmKZRAYEAUFAEBAEJgsBsUyTxQ+hRhAQBAQBQUAsk8iAICAICAKCwGQhIJZpsvgh1AgCgoAgIAiIZRIZEAQEAUFAEJgsBMQyTRY/hBpBQBAQBAQBsUwiA4KAICAICAKThYBYpsnih1AjCAgCgoAgIJZJZEAQEAQEAUFgshAQyzRZ/BBqBAFBQBAQBMQyiQwIAoKAICAITBYCYpkmix9CjSAgCAgCgoBYJpEBQUAQEAQEgclCQCzTZPFDqBEEBAFBQBAQyyQyIAgIAoKAIDBZCIhlmix+CDWCgCAgCAgCYplEBgQBQUAQEAQmCwGxTJPFD6FGEBAEBAFBwFdpCgqpozJHH/mivyuVZVmSJKlKPeU6yjHXVBpFyvfseU5HaBiYPNfLVBZFUalUajabYSEM/CBJkw5tA5/a+EUn6+ZhT+0xUVnghWDVjBuOKkTNeqahCVKDZ/eZcZ+ljmtJah2VsidxEvlBQGkGkAzGwT7PdfOmZ9T6DZSrOIp8z1OZixCSrAy0jlQlz+S5RS1XTVUqFppxGvph4PlarhxNSi/UloqcyVFarnzNR4QcGhB4yEP40yEFWwpzRChO3K5coRy0XLnIVYtLWjVAA99JnA9rv+Oi0DXNj1JEXw2EtFceNrW+8pWr3SaMD9WwNelU2DbOJEuyNAtcP0tTJNLe37ln7Cdn0dDJP4ojSg+CwPO8jraFQtfJ2e3rIcgoqxZKxohr6iAGkiCMtor6CF2tVvJL1NaSYZuoLshQ6GbaCAFGnMVGO4CN1q2aZROWWnKlkixTnuNDdkuusnbVNOEtnPPmb5RFFDFQrjpQ9zYMC35+iDptC9SVK87S1Jqr/nJpufkm5IzOlufGSZzqPmpbrrTO0AmU9OW2lOVOj5V20VfDuL5V9JUfNxrUEdeDPghHlJrt9fi+T48bQ+Q5/KffhvBp6WuY+4fBsvHr0DAwof3pOeIwkdAj9h50St70nNEHsRrTHP1CaGmAGEjSDoryMifLm57YCSxJ8ATtDS2u0WV+SfuyaBHPgWM6FQoF7FLe9JiiRjggV8ZaupBrtZiWMsfVcohxNRouNerfSkKSRSPkPvqtToizNkiumg1tmUw775eB0ctZ7xN+2CdXNL8sazR1O+1PRgz6L4/tCsEJmxftDwOEa4RcwbJGQqhAJw+z1faZQGxY+7WZbPxo60spoq8Ggtkvq1pHKLXp9JVvW4Jv+iCJCeXZ6MnJkyexTPQo6TClzQh1QmepoG9vSepAXDZ+ERoGpmqtGjnR0tJSHMcrKyvlcpmmQost5kxPb3/ZBjVtp6SeRAASpUm1Wl1cXFxbW6tFNeiphOWB9I/rIgq9pRE6naNM26Q0iaI4TlUSqdQNfWDUWKVp3vwatV7IlY9cqQgxSxtxoH1wL/AKWg6pkambbUtWEnyVr7xVm2fLVYDRTDM0srZMtnodqPnaujRqvdd7fz3WckVHpytXdS1X5dJgudK8zzXhK5GUjpy4hYBuK3KFDxd6YUsOMeyg0oYITZJvMgWJvhoKcpsR+gbDC3th0+krXw8dDfKZZmZmsEyBQ/SMLmWrn86dBL51nXNLw/pctmVikCqVyuzsbCfIkzc9nSZHja3GtEcbXXFdP5gJIAndUQpK3JM3PR2fKdUSp2mxPpOLqsBUqxR3krEKtCocxDLlTc+oggBVWKZABagzLyxopUZACG8JuRrkM2U5+0zlgtb4LbmambXRajw3HT1uK9x+GRi11uu/38YDfI9Bw7ZcFY1cxYPbnRGD9Wc/8p3IOUOAvZYADmKZ6LNaG6R7rhPgM4m+sqztl9VNqq98O7xJXAVFR1PUPVlTRfrajXod+aMj7tKF9ALdc0rTQlm3k/wSNAxMdlCaJkF3sl6v0245h6SZcmXg/WO7OKQPslxb04Epz0X1QxLEmBaahe1I49gIODMj1IHVCCasYU6Nz1SvrRFu9QKXzhGzVjLXhaqwWLSa7sw8LuY35KqJXKH5GV5KVNELcPYyTkolRNDG92xbspLgq3zH7ao6/uS05Kqh5UohalFcKVe0ZbJQ9clAfgguV7VcES7ryhXDvFlrWkR/uXn7TM1qDWKcwG/GkR5n8rRcFZErosqGGt1zbZtwLlgO9tM5tiuGF6KvhuLZJ6v2wqbTV/5n77yTSvbHbQ8fPnzs6NGvf/3r9ZU1lGAlLNF6ma5XYxpTnmmYz0Tj3L1799NPPz01NfXggw/WajVaCHEPIo15ktMNU1CK1ZgtvVkIIMnx9RDFM888s7q6et8D9x07dqw4rAJjorLjMxnLpGlpjTMVsUuMManVRi1xs+JU5fHHH9+1Z8+dhr9jKnwM2SBXx5Gru79eX13zUmcqLGGWUqZtNJsDfSY/Z5+p7p0tVxmz0ZSeFKctk2nW/f3QMQAxJAsiZsgVkequXN2n5QpRH/iEEYOBv4znYiko6LC551brNUS7ZORqD3L1uTtblmkyxplEX1l+98vqJtVXeOqm12VGFOkiIv+2Cezdu7dWrWKN0Lm+chjc123DzEMbj8gPy2VwA1Q0zl27du3YsQPLRCeOKLz2CULm+ObbaxzGaXxJJhdgmQjlQRV9bRTKqVOn9s/vHlazsVzPmOBg1GWPZdKQxYxPwK0oWauuxY52baenp2Fii79jKXscmUBSvSNXGTM+iZx5GCdNZ8ZYpvaUWlrYSILXnqs2jsIH5HHq1NlyhWUqFoiMehfFMlm5ovSz5Ipu2QDqiYj29pEH3rGxi4QlEKs4yhhJZbQp7JGrlmXCj2o7u4Z5Gyvv1Z5u1Vf01RCgtoy+8n/09tt1HftmQDzyyCOXXXbZD73zh1D8ehzAWl5z5xBMxnN52AwIQizMzfv85z9PJOHtb387BpSRAILg+dol6tTb8k1btBegM0oiposzbfGrd32NCUtve8vbbn7LzWUd28gxxZpXOnVVkiXIrChhnAn1QTwW8r7+jbtRK7db/uZI0WhZ3/UrD2i5eoeVK0Wnx44z6VyoiEXYHNszIEbLf9S7ieYRjmrJ1S1arpIkKng6hKgtk82uTwZGLWX992u5MoKNXH3ta0aubnnbzTffjPAPzGTw1YG3nt9FW3e9SAK50nPz7rJy9SO3t+QQUQSoDkQtyM6vsHU81aaHv2DVGX0QfdXCrsMIvhte2AtarjaVvtK9HEmCgCAgCAgCgsDkICCWaXJ4IZQIAoKAICAIaATEMokcCAKCgCAgCEwWAmKZJosfQo0gIAgIAoKAWCaRAUFAEBAEBIHJQkAs02TxQ6gRBAQBQUAQEMskMiAICAKCgCAwWQj4k0XOBFLTuz7AktdasWGXUrC+iG3YI/1RfFg2kPsKkwkEaTOTBNdYqAMHYZxdLQZn28lyv1cG8l6v0y5Z/goC54NAr6za5zenvhKf6Xy4L88IAoKAICAI5IeAWKb8sJWcBQFBQBAQBM4HAbFM54OaPCMICAKCgCCQHwJimfLDVnIWBAQBQUAQOB8ExDKdD2ryjCAgCAgCgkB+CIhlyg9byVkQEAQEAUHgfBAQy3Q+qMkzgoAgIAgIAvkhIJYpP2wlZ0FgmyLAWzR7a65fh92+cuTIEX5qNpvLy8u998i5INCLgKy07UVDzgUBQWAMCGCKeOMzb53m5by8VNP3fd5JPTc3xzlHCuCENIaSJIstioD4TFuUsVItQeDiIYBBKpfL09PTpVIJswQhvC0eU3T8+HHeSY3Rsg7TSy+9dPFolJInGgGxTBPNHiFOENhcCKyurlarVXwmSzZBvCiKOK6srLz88sv/9t/+2xdffDEMQ/vr/v37N1fthNoLhoBYpgsGtRQkCGx9BKampvCWiOPZqrquGwSB4zj4T5dddhmu0re+9S1+mpmZwYZtfTikhueLgIwznS9y8pwgIAj0IfAHf/AHzzzzzKFDh7BJBO7s3AeMExG8K6+88jOf+cy3v/1tTNSb3/xmDFjf03JBEGghIJZJREEQEATGhsAHP/jBF154gfEkrBGjTRgkHCaMENG8xx9//CMf+Qhm6bWvfS3lYbqI+4l9Ghv0WysjsUxbi59SG0HgoiLAfAdGjw4cOIBlghAGmUiYH0zUJz/5yRtuuOEDH/gAobylpaXZ2VmcqotKrBQ+uQiIZZpc3ghlgsDEItBIGkVPT2Roxs2Sr+d/R80mo9aLqysLCwt8Zb4D7lG9XrdeEe7Rr/3ar2GQ7NdKpUKgD6PVmQ0xsTUVwi4KAmKZLgrsUqggsLkRCI1ZSlVaMGZpdWWFqF1lagqzxCpazjFL1jGinjhMRPaY/sA8CObp8dVOixCztLmFIE/qxTLlia7kLQhsUQQylTnK4diIGuUgZEoeI0lxo/HEM08/9NBD2KE3velNb3jDG6g9Ux4+//nPv/e978Uy/cAP/ABXuBObhH0Sy7RFpWMM1RLLNAYQJQtBYLshUI/q5aBErdfW1spzoXIc4nX333vvsy++8Au/8AtMdvjQhz509913/+Ef/uGJEyc+/vGP/+Iv/iKm6KabbmLtrV3txMxyvCvZCWK7Sc466yuWaZ1AyW2CgCDQRaAY6MkLSZoQoONkeWmJJbRMt8MsMcJ0zTXXvO997/voRz/6ute97ld+5VeYqvfd736XOB6b5l1xxRXWMmGT7PYQ3UzlTBBoIyCWqY2E/BUEBIF1I0Aoj0kQGJvAL6ZZeu+99+ID/ch73kMG+/bti+PYbpqHocIOscLpwx/+MBf37t3LDRLEWzfM2/dGsUzbl/dSc0FgIwj4ns84k81h586d+EDs98BXu1CJUSXieEwN5+stt9zy1re+lZ+YGcHRuln23D4uR0HgLARkd6KzAJGvgoAg8OoIrNRWPOX5yl9eXXYd98033PDG666rrTJHb4WH2ar1kUce+bmf+7k9e/YcPnwYt8lO2FtcXGQ4ihusR/Xqxcgd2xUB8Zm2K+el3oLABhCYLk3XolopKM1MzXSyKU1NKe0UKfbEYyXTJZdcgh1iXS1uExE8ruBX2fVMTN7DXOE2iefUQU9OehEQy9SLhpwLAoLAuhCIVYxZsrcS06utVfWy2SDIPBcL9LnPfY5JEMwaxw5hgewE8d4dHxigEpu0LqC3601imbYr56XegsAGECCOx9PHTh0rON7uHQvlSqWVmaN3JGJD8UsvvRRXiYvWYfr6179++eWXE9zjCqG8XivVelD+CAI9CMg4Uw8YcioICALrQ+DU8ilu3D2/e2GH3ovoU7//+7/8iU88at5w8dxzz+Eksc6JLYhsZpwz7HT06FG+EsezFotzbJi9QY6CwFkIiGU6CxD5KggIAq+OQMe6cOv9D9z/27/92w8++CCTwp966qm//Mu/vOqqqxhhsi9WZw3TV7/61euuu46LbErEg51nmUf+6iXJHdsSAYnmbUu2S6UFgY0hMDc1RwbM0JstTTFl/J3vfCce0sLu3Y88+h1Cdj/8wz/8e7/3e+wEgRFi7jijTez+YOc+MMLEQBTRPJbZsh/ExqiQp7csAmKZtixrpWKCQK4InF45jXVhye2VV1z5Ez/xE/fff/9//I3fePs7f+DWW29lJt7tt9/O1g/Hjh1jG4irr76aK0yF6KzA7bhNuVIomW9eBMQybV7eCeWCwMVEYMf0Dopnu/HlxSVmN1x58CBfl1eWMUJ4Re94xzv4evr06R079G0kRpVwmDp+EvMg+CobFFlw5HgWAmKZzgKk76tZn9G62nuuGKLjA4BMmg1UlijFAngZt+sDcMIv1IqKkFL4lCqUVRIoBj5SX19R39OEZ69B9SqP3QvWUK1K/7xzwis0XvLYGY85C+SZxom1IrXjp/UbmOp1lx/MdIb5uZbtwSti9RI3d6bedcwSF7FYvbTZbHuvyPkYEOjVUb3nm01fiSYdgzBIFpsYgd7Wy3nv1zP6GbQU+9nEdT0P0vF+2L6BB3Fx7OPYHkaMsD32HUv4PRgkjvwqMbrzQFgeGYiA+EwDYZGL2waBM0yRsUytK9ih9m9oXYeWgve07XpynZnf9nUVGCEkw+4wZEXEXuFcVs5umzZzISoqlulCoCxlTC4C1tZkxh/CEvFX614SIaweO0TAVtup1m/mhu11wPDwjlpWJjFcxOZDDCAR3MNckTo2Cc+pc7690JHajhsBsUzjRlTy21wItPwiX2W+tj32o6uAWdLjKx3HSY8m9n7VX7Z+wg4Ro8MmYXV4mQVbsmKTsEzf/OY32UecCeK7d+/GOFkgmHpHiG/rgyI1zB8BsUz5YywlTDIC2i9iflnYMjx81VeY6YCGNbaKUF7rVQ+mGi1LNslVGidtWBridadM+tKXvsQ+Do899hie0xe/+EX2H7r22mvxnNi5dZxFSl6CgJlaJjAIAtsYAWtp0rJKeUkrg/yecuxQP35A22c6yzhtM7TwlliW9Pzzz991110sUeI9F4Ts2Nbhyiuv5KepqSkmRNgpeTLdbpuJRo7VFZ8pR3Al602AgLZMrkpnVdoKSRmHCZvEFOc+/6jXedoEdRsDibhHmCLesXTo0CFeo86GeLt27SKOx7pafCm2I7riiis4YpxwnmRu3hgQlywMAv7nP/tZThJHZY4+pubDFeTsuRdf/NJXv3Tq6HGCGjPlKT22iTC6fc11rFBCw8BEr42V5AQV6KPdfffd9N2YxsoKicDRwZf8ktOjjICIZI9Rpvf2d3yPhsrrO4m8f+P+bzz55JP753fnRww5x05gSfI0YZoWN9PD8okTOa6bqmSpuho76fzuXeiRKw4e/Kzhb64kjZQ5cvU8cnXXl04dO+5n7mx5ylUei8E8pCtzU8NN3ttjaqQz9rN8N/3MirOnTi6mzR1eWP70H/5RZSqYLldOnThdKk67GbIeM/7k6PVqnh6IAmxf72SaX7JyhfPRlat7tFwxnDOwUCMGA38Zz0VaGWNLDz30EC0O+3Tw4EFid2w49KY3vYnGiH1CLSD8bJGHWSL0hyUbT8FDcrH1FX01BB61ZfSVb5cp9HP6lVdeoa+EtGEJkIZiWMQqZUlSi/TihvzSMMs0Pz9PG2D0lSFZKKGPBuVcSZr5aq5hnPYLAeoDywQxdkwYYiDS4pknPm6LpLZlYj0JxflFn5WPjhfETpagU10X9sHE5Mrr8yPmPHI+Q65SB7nCLKVOFrNohpqYuvVaJmpzHqWM8EgcTJUveeqxe2Zmm1e/7krPY2OCtBiWk9hniY7jRMppOElJZXhULKl2s1asb4QSRrrVyhWitV656uk5jVTQOm8mTIdI4yQhTqxhspMdaH0nT55kvoPuGgYBJ1gvVj6RZ+/S2nUWMdptpr6ir4aBtmX0lX/7HXfoStJhNVF2lJydGPvEE08szM+zBZYTp26ahag8NgZO00I5300Yh+kh1qKj+r/whS+wwOLGG2+0A7OQNFNuvxhmGK82eL235VufyWS4XFuj+688F0t57/330VW8+aabUV1lOzixwUKHP87QvKECR6N9kzmpN9bwmbzArSdRSv/edb/29bsKxeIdlr/tey/63wee/85O5Orttzq434kqegH0Yn2KbO5JRSzC5mglIe9w87HTarqiPvn/PhQ44Q//0G1+uMZuB25WKocFnHHHNfs+ZIY2C7gZe8oPxuWqlis6FsjVffcZubr5ZoZzPHdwwYOvjo8+el14SFgd6KGTyqrbF154gXbHFbw6dhB/73vfe/PNN5+1v8P4yu/LyXJB9FUfMK0LFh/7ZTPrKz81r0jp74MQqqLjFjiBF2hdiykumE1KENBhmIzl+jCfKfD1bFRaLFTRd3NN2CcshHnTM6wPUilpi4gV90Io0q+ccc2krrzp6UTzUi2C3Wie1uy6V58WXS8xeyVBFUzMmx4KHSlBko9cqcAjiuc6iJYfEitztRwOiuZlOUfzZqcD5j28/HwyPdPERCm3kmWJ73hRTRHLc/yGcmtOQpeDyXsYfJWl+cp/pd3T0lJl5QpR53V88eByjRiMxIHRbsYHmp6eZmktITs2x8N/IrSIsONL4UgRJMCL4ldsJ/lC8Gi5j373sGie6CuL5ZbRVz6xYapEI0Sy6CR2fCbGTlC3UUboTDWakc8tjlPwfZyV0cVphCeGjRpVa1UIoA1wZHUF8QSaAe2BPVJGyP08bh3SB8E1gZIoTSAJh4ljLapBzw62X8sz0Q0yPSHrM9lOkVYHaRJFccw4U6RSN/RxOOBgnKZ582vUukIVHkGkIiSt0YgDOhvKC7yClsNMyyHJjuRZSfD17O0c0/KKShrqpefisFRdPKXmdqrTp1amy3NFLfFYJghKGV3SqHPQjSRfeuqxlisMQFeu6lquyqXBcpW7KWBoM45Zt/T617+eV13Q0YEwdmXlPRf79u1j1jijv3ZiHkRCeY6sslmb9ij6aijOBp/Wr7Y1mS+bTl/5caMB5f0+E5s2sh+W9pk85ZZ84uu2tvRNWtXO588wn4mume/5dNMIKdCJ4/zC0DOsDxIU9PaUrut70x7Dv0RgSkEpVsCZLz4dn8l0Hrs+k1/Szhs+E0tGUfqodbCCvrzpGVUK9GagyBU+E0SGAZNrHIjNXC2Hg3ymJGefKQzCJ55QU8UDcbp45LC2TFNTs8VANdaMZQrryl91CKEScNTzIDrtYNR6r/f+wGx7injT8WrJVbEUJ3GjOViuukHd9ZYw2n06GOC6WCasDiRhpVhvSxvEf+K1TLREDBJDYtxjzVLe8jbMZxJ9Zfm6ZfSV79uW0Be3RQQT3QdPGZfOUoYtfATQybK8A8rDxpmIZjDUVKvVaB503KxlSrM0b3p0N7mTevog2jVph++gipQovat/3vSg0G0foauSiDIZn0nvXOZCRKInWCqHIQFXs/eMDZ47VblYJ8gVb+nRcqUFS/mOj15TaablEKgtwubYHmfKl/5GVd311ShpVk4tHvvG3d95/fXXRc2s5DthQXtzdMz0qiZ71PvKQ1m+I1/MzbORaoS8JVepkSvTE+rnmub9BUlMDsT/xpnDXuIk3XbbbXhOnd0fIAE+knKXN9MecWX5i4R0Yjyir1pSsFX0lY9AaamC03bKuGG2raTWHLRL3VXScQw9KZnBAG7NMw3LnnEmgvw0V9oGHbQOhRinPMkZOgsTYqwahRhIgjAMFVjROHOlh3nVtlvUOqIsjSyCA5FW7TM5hPIApbX9c970nEdlW3LFqIQJ/gAgvSC63B2PxMpA65gzfzEETz35ouuU61n29FPPx/F1DO5QKctGbeKZqK91IKAyg5y4Xkv2zqPi63lkgFwxtup6w+S8t4+8nvxHvQf5QbYxQnR77NRw/CQGn5iIpGcA9STrNuUtbzqwKvqqB/azTnvlwca5WsfNpq+IpuuWZuO2Z5hb47xbt4DWQshd38ZgQL6GSXeFBib9nhimnqF8s8z21PCiMFf56glI6TE0RpG2RkE8lUaJniRSINKpmkEBYGLcptBlK4EcE/W1ZNgmqksykDFgaEvVqk1H8/RUEe1Eta24/fWiHyEJwjpyZb0kbKomTM/S1n9bo036lPMOAyyrCf3pO5eXVKlonBm+ckummCKAOUl26KG2gCkDDfX2t/yDz/zJ/75/v94oPPVqvjoZqZONqDEd7FdqPq6HvqteVOrOR5ZfXC0Wwls/+fsr//RfqiPVR68sN/zSASfZqerzyufzZY1o9C7VUM60ISu3A51AK9gIOaKOwNP0rPAPLNNiNfCnsVzEgWvFJ+ju0Icg06niUtKIfT2WSTJOZat7BKl0nMzl3A5G2kVfDcW301zaisJapk2nr3JX7EMRlB8EgZER6IorL6jT5sxRx4+rI0f1CZM3iXgxE/2px/Q2Dvz41ptu+zf/218ePayOHcF0MXex6KiwGExhZtKUWLV+6oXnVL3KjkSlJPHq1ezoUSaRX5IquhftLSG0KiSiWOJm/ZEkCAgC+SNwhj+ef3FSgiAwKgJda9R9ksif6Ts//PDLf/jpP330O08XwxkWvB05cqzWPPi6q67znfk0Dl9+Mb3r21+4+c3v+umP6hkMzazs+lP4IFgmIlTW0tx3t1pexOpMJ0lcXVv90hfVR35+Z0NhrEpe1w7Nt4ruXunSImeCgCAwdgTEMo0dUslwvAhYy9QbpNCxu5UVBj+CAwcu+7EP3v6e9zR3zO0uhlO1WsMLSoTaX/6eevCB6Btfv+dDP/rBd79bYYYIt0ZRVvTNVg4qdJSZBJepu7+qaktlJyNI14ySyte+vPqRn52Kk51ZgUG7jo+EZWJOiQldjbdykpsgIAgMQkAs0yBU5NrEIdBrn/TK05lZvf5p5261c9drmCSxtqpnfYRh6ciS2rNb1TA5v/nv/sm//G8++tf3sJFbwFogZtM364xycRY12SujhK1JmuqRB5WqzWQsAWM3injmW988lEZXB34ZS8i9enqehmJBz4AQyzRxUiEEbVkEBoVKtmxlpWKbEAE8FxO46yEdq5GuVdeOHD1x4uQKBoO58uzdU5lWhaLac2l6YnXp+29Wf/Pv/tB7PrCHEaLpBXVyicVAseM2PT1gHzbqeiYglunZp9Wxl8m/ojfKDULfKR16afHF59sTgpiZxyx8PTOP0f4w4ZynJQkCgkD+CIhlyh9jKWHMCGjLVKmEl+yd37lrWrsyOjZnQm+OevHYPTt2sN316sFr/L2XqbVmY6W2srATOa8y9dqsRipEDV57oafwPfjAU6oRse8WE+KYAs08Rratu/9ePYiFNeRuXsKuP+Yrc5z0O9klCQKCQP4ISFPLH2MpYeMIdN0mbS/4LC0v2qWWLPSJ4oxhJNymai07sPv7PbXwR3f++c6F/UmqKqVwujK9uLyUaEeIGXdYMBYeaLFfXVVPPvVd5dSLei1vg589lyjg4pNPntDT9nSK9eIls6ZJG0O9o9Ky/UGOgoAgkCsCYplyhVcyzwkBXoNi142xxobZDXowCDvksMirUfnNX338b/+3/+mf/cPPVE+puKbty0xpp5dNpdHMyjJ7mjAcpZflTc2ov/jSH6nsWH355dm5uaXl58LS6vxc4TN/8ntJrD0xpXitQ2sKH18yPXq1oi9LEgQEgZwREMuUM8CSfT4IsMia7bOWV5bZhMmWwE4lpZJ77JA6faxw/bXvuvWW26anlE+gjoXQ5pawEExP6/dZsDvSqVPq8SdOOF5deUemFuK1lcNKvby4/MTpxccqlVptTVsmHfJTBAaJ/emk3yKoN4OQJAgIArkjIHPzcodYChgfAtgIrAVJG4soahQC3mVXNLYnq9d4kV2we6/68M9c+1MfufbyK7UxObWodi7ofYWq9SavXIriJPC92Tm9kcT8ws7f/9R/8neFf/5Z9Td/5qnLdr3u//ndS258y/trkZpbsGE8SmHqBMeQ/2w5TsDPlL929PQAADfySURBVC4HQUAQyBcBsUz54iu5jxsBYyNUVm80SkW9mwM2hsQy22IxKARqua4uu8LMhnAVG8cWp1eV45VK+Dp6t1u8peWVLPQrgc++TWr/gfBYrPbuU9Xmc6un9wbeJYxXhVNq6XRt53yJDSNMQC+2syGIGiqV82sqxw2W5CcIbFIEaOeSBIFNhwCvaWeNkjZLi4u1WlUxiwGzxNeTKydxbBK3euT0d3335XJ4tKGebqjvKXWSSQ9hIZuZKYYlXqirXnrp1PJytrikpipqxp2eqQSLp9XRVxRbMe7CLGHLEnJkZS6uUsrO7sxLd9TcpkNKCBYENiMC4jNtRq5tP5rNhITeUJ41S/U6ezWU2NoVm3T0aProo9/NSoUkKuzfP33JDlwnptLFSysre6YvATJeV1hg+zvjZPmh2n/5vD511ctPquX0UHHRmd+hXsP2r058+sTRHTOXapTdUDn6xVHcydayOpYn8TyNiyRBIF8ExGfKF1/JPR8EXHYWr9XiYuiUSwTp1MMPH/rG3ffzOtqHvzbzd37uv3zm90+pqFRb23Pq9K7Z0vcrtU/v45AQ/QtOnDxx/Pgh7M3S8iHlrmGbWHW7t7h/bmqWdzWZuRLVHQtzejwLtynlrVF6s4nW19Zs8nzqJLkKAoJAGwGxTG0k5O+mQUALrVkY2/L4H3/8yF1fu5utiT70oVv+x//+kvvuOvqFP30MF6kUqPnZCqNKa1W31uA16qu4PDsXds7twERF5SkvSpbIYmW5vlJfWlxeTGPFCwPj5rLizFojvY7JlMJXe2XToCSECgKbGAGJ5m1i5m0L0vXcBQwK65IIzWFa2K+VaQgLSebXanpWw+lF9ak//exf++s/cvlrSg318lPPXpZ4+09Xk9hXR5cb+3amvMspKCdFtTC1sA9zhfcTOLOcBCzNdRtLuFGzRV7CVE/0tq4NX0XNSyu82cpECDXCTpA5ryjXT9UunpVg3raQOqnkxUZAfKaLzQEp/1UR0INMCCpGgSkJ9KW0dcDgsLQWo0Us7vLLL5+dWYiVl6jgoYdZrtS8/vveyE8F8x5knrUvKmyV0xqyMgbvVYuWGwQBQeBiICA+08VAXcpcPwItQ4I1si+wwBwhtBkOD5s4YLCmZ9Vb3/qW+TmmNvBRf/HFhusl73zXTs5ZeMuOd7x4PlB4PEq/b4kPQblukp5ZFws5EwQmBwGxTJPDC6FkEALWMmU+r501nhMmBnPCUXmB/sOb21/72mlrb5JEPfjw13bvnnrT92kbVCzgXrlNFQe9QTibIUdCgTorSYKAIDBxCEjLnDiWCEFnIKBNiLnAHDnFzAU9vw7L1EhO8WIlTpp2vhz74UXqhafViZPPXX/9FewL0YyMk9TauKEt5x2z1CrDfj+jQPkiCAgCFx2Bdou96IQIAYLAQARYRkTqzJTT24Rry+R67BvEhIhV7RSxaqmpWBv7rQfrnrfyAz/wJgafuGISg0w+rwDUeVgjx6k90Rf1dUmCgCAwaQhIy5w0jgg9ZyHA5DxjmTrGyZgTrJPxmWoFPXykfAQ5Vvfc9XxYrN56a5AmqsjerXpICXvEGFVbzq1Nalkm/rSv69wkCQKCwKQgIC1zUjghdAxBwPhM9jcsjf1oi5LWMjYCTyOieGaeQ5aohx94xg8Wr7paEeIL9JsuVCNuMgUia1mgtOU2tewTmehpfpIEAUFg0hAQyzRpHBF6hiCgHaBOQm79RgN3yg+cMpbnyGEWzKrvfPupH33fW+sNVamoUyf1EFPZL2cZAUH7sDFyLbNEVq6ZBNHJU04EAUFgUhAQyzQpnBA6hiDQFlFrUVo3EcwL54rsOTT1zLOvVFfV3kvUl7/M2qbsmjfsnp3Vi5yI7/EE5gfLxFAT3pWxT2wczlIoncyxnbm5IgdBQBCYEASkZU4II4SMYQgY+9JxdMw3Mz40c+QYkxxKV7xmL1vnkX75X/3m7I7CW9/6Oj/Qa2uDQE+W0Lcn+E5WzrVxYnkTH8wSDpQ1UcMKluuCgCBwsRCQ9UwXC3kpd30IsJKJZA0Sx7a/k2ZufXVKb9PaUPWmataUX2j80HtuuurqnQwecWNY1M9ggvCZjCXDEtmPtlK8BtAcOUgSBASBiUPA9iUnjiwhSBBoIdDxa9xUObE2KMY+rSyqD7zvZ6+75mdPn9DXfvd3nzm1+OJll5dnZ/iaZknGMluuM8PBcwn9aStl7BSmylirzlyKVjHyRxAQBCYIAbFME8QMIWUAAlgmPtgk/eLzupkprq986+GTSyf9/XvftGen+va3sEy/8xM/9f5//L+y90O9ES1n+madGHAqFEIz84FvNq/2N3ODHAQBQWACEZBo3gQyRUjqRwCjwj7hDCyxex4rldT1b1z4B3/vX9xzzxPve+9/vvraA//m//gX73y3OvyKuvzyyHWzgHfQ8iqLxPHYNZyRpjRl5MkkzBLOlxinfoTliiAwQQiIZZogZggpAxDQDhOXsSW4TUwTb728b25WffTDB//Wxw4eP65mFxRT7rht32UcUl+vveX+tF6PKhUzO6Kbr7ZM3W9yJggIAhOJgFimV2OLHaGwd/WeawXHBwAZZOe1pyhNxjNE670anqP+3pLQkDkNXSb4+s2BC/v1hUvnzswx3dXhwVTZhznMzCu4hbVm1fcLjhvy3gwYZjww/eDOleB6V4Xx2qya2sHs8nojLB1Xy66K9mnrFi4qt+ake2GsV1rkNVGZ0ruYrz+dVitrS8v7ZvcktUahWKqdWi7N74iSKPUDbCxzBY0YNYMs882cQS8qeLyvtxRDZpg2srThZZEXMcYG1YygmRd6UC1PxyvxIqfXT4rcuR0Q6NVRveebTV+JZdoO0ip1ZN9xXgWo6mndMQk1j4nylHfkmHp5BUcsWFPZibpa85MZ/K6ZsloxHlrB15uZ0+vQUymCRMWtVVLrRtRTJd6riyXUvZbEK1VmyCPApPhYTCwT1o/EywmT1HH1JbsrhbFXkaf4aJfRXoQMzvlkrb/2sslBDoLAlkJALNOWYqdU5hwIxGmcpmnRLxqfqXVj6SBzJlRUnErCrLpTrQXFhvLXGquXVOb8hPfZYo3CKNAOSk1VmGu+T3vJI6RVFZW0g+fU1pYL0zNquaFNXVgixwKGxXfZWwmHKGFFMNbIyQp+HCXaJcJ4rRYwpXrWBy+jKmDc7IfCOUk7S4lHIEZuFQQ2CwKdyMdmIVjoFATOBwGsURzHAatwTYpU1Ej1/L3vHV49dEQt7C6FlfTlw4dOq1Oo/dlwQY9TOThLHi9nJ+xmIm9YCz1qZdvMOo917RUxH8Odm9+lLQruD/mSdAHm0/KJeLehlzoBdqjq6dd76GmIgar7JmrHE5R3ZmPlm/hMGklJWxGB0TqAWxEBqdO2QADLVCgwr08nbZYaDdd1Eze5bu/U4QdONg9/hz0j9hd2X6mKvlrRrQLjQPQsJJqXFFPicKrh6QvYA0Z8CLut81hySsYQmSgcD08XVbWu44hkgWNkIoUYLGN69KsM2aQWm8RXbCElNoxlwoQxyMbLPHTxfDHJfmt9kT+CwNZCQCzT1uKn1GYIAkmSBB7eT1xv1sNCOBXyBkKUfLqqTt333c8fjR9ScfHJF9UN9TcuFAPfTizAYiRmsz3tzqhyxj5H2maQMEvrPFYct95cra/U9u5YUM2G3gJ9ylcuNi5JXYJ4JI9GiAHUeWLzmGphwnUUZMviDn7R9siaJY4m2YviNrXgkD9bC4G2mG+tWkltBIGzEIgiBm7Q9Vrbm/lt6uTyyT/4oz+YfsvCP/3UP1GvW1WvPfK//O7H3/7hH/zlT/7qCgunmDCBnxIwLMTLcVtWQreWNB7pM6Wi3QV/7/wM2yg98dDd2bGXlFNtfRjVUvVQB+2aDpssRXwi5tpNpaqiVJm3xUdMGtTjWt1Wyhk14GicLfwqSYLAlkRAfKYtyVap1NkI+MxCaFsmTgjoffrTn/6lX/ol99YwXa0Xi7XA91ZWll565uSv/va/K2bzH/9r/8xD8WcN/Rb3pKjYvo+JClgFPRI0QsqatdryWnlmTi0t/4ePf3xXqfLed//g3M4dBz/0Y67P3EBcJI6ezh9rgx9UD4p4UiwmdtU0L+rFOJnSur4RNOgBMB3u49iaSj8CRXKrILAJEGBlBK1Btwhm0eqj+XBlcXGxXGqtUmToWMUpbdv1vMzcn1/N9Pabg5LnekmaQAkEVKvVSrliR7PzpsfGbSxFGikDlPnrEB0ixlKtV6EBwhI9GHEB8DF8ggxDjUbLkoWeSpIoaWY+AyhaC0PS2spK3vgYKEY4IFeVjlyxS0OcBl7BI4ZFfdq878V5VPqddiYdYGxuBb/w/IvPHzhwoFwgLKf59YlPfGLXrl0rl640V5v11UeZTh7uaXj4OIfSX/5n//zvv//veMG0Std4N6EeDlJTKgu1KVhYHqG2hOkKnj8fqsXTarWx95nv7Y2DIw8+/cLK2j1/65/sev2VV73jlivf8RZ1/bXqsr1MbNeGajlgejo8ddJodxZ6zUaYIfiZx08aIj1hPHb0Zk3sh4H4jYrPSMRzs/Yyk6SRxA5MMvNHgG4FuWqLHfDy6TQTi/aopaz/fluQLlT01SDUOozgR8uLdoPYZPqK6axauZkDMtj6cOXSSy9t1HX3MMkSLZNha1ITq0G4mF8alnsUR5giVEmlUgnDkMZqF6bkTU9vTXurbpQEy2sziIGqcrmMWeL9qqHTAqr3wTGeax4ZjPqB8tBeXthEkWgN6kHS3Pz8hcRnPdVErppWrjDkrlsoBPoVFVq3dWvVc8rl/oqes5ye21uPtq9cceAKBpboZMGpL37xi+BDZ6t5rK68uvK1ois4qyWPdxGqgu/c/Sefee3Uwv6phsO61yhU7g7lz6s0bEw9fc7iz/7x0KFDl1Smy25JHT71nksurz7zolNfQUTKMztOfO/Qvb/9e3/2n343W9ix6+CVB95wzZ79+1/7wx9WM1NqBqcpLqw2/UbsM4XcvFFet06qZKqjbZKxTCPjczaBr/adYjwv9L04TVAFjqPlah65ajGsrTHaII/KrlcrfvDvthTKtB9uEn3Vj1QvLzadvvI/e+edVCmhXdI3YmsX8+HK0aNHD7388lfu+kp1ialKTikImc6ETvGL+cYPoGFgoqe2d+/ehx9+mIZx8OBB3CZuQ7OkTT1+kF86ow9iaLN9ELcQQBJwQc9DDz0EPfc8cM8rr7xSGXG9y6iUx05gSdI7wxkvw2U9DFPJorWwyHLSoBo1Yictz0w/9thj+y677E7D31FLye9+5OowcnX3V6rLK37mloOwWY8atWYpDAlgsdqUolPTpKwk+ATTRklO2u0ZZAYp/UpbpY6cfGXPnj2pm548efKN17/xd37nd+r1+sLCAjBWmCinFqNqFtbVHBPDm15Q9//l3/qfrplZuHwaW1SNVmMnrrjuTicrL6QvjkKOKlezl2amC1m6dOrItO8vxqcRopm5macXD7MHerk0dZU/FSypwv3f8+49vJL5/+q3/lyVCnNXXHrVW77/e08/G5WDb993/xNPPz0zM0O4jwVVwBK7Litwm8wVdNQOVjzlmeJ6o1hkDVhYbzZilVWMXF2GXH3uTttSmRuiJ8UbKmDesPY7LhqN2Iu+GgrnltFXOvRDLXWP0Xw6nRBcAWbZBkGge+KEENrJ3j8UmA3/YPV+fzaQYUngBKqgjVWTmhhDf//947oylNP4kQxd8IoFA1GHNrNgclyFD8jHdVxLEkxpWyZ9W5s/bCTgei4rRDVEMDFvfg0g8ZyXzpArTFA7aToZWjGWyXbHWz0AvQB1hNR+SaB+pG2Z9DnKFNdW70/u85r2RqlUWltbQ4TCEBZmBBXtsA39CsefTd3MKxb8ctGrpJnXjJrNzInosxE789gFYpS0Y8dcdWV5qbYUqGQlXplTRc93k0a8f26qkTrVZryyfBpOhqo0oyqOU15r1jM3KTQbzNwLK2W/UvCDIEoTw0f2qoX/wONacHCNcxb/M+XKYWphV66sZQIORNGCwnFY+x0Fs3Pda8Re9NVQiLaMvvLfd9tt1JK+PyJFf4euj+2DPfnkkwTlb7jhBhUlgeNWiswV0ik1PXR7nsdxWJ8LPYJ3cs0119B5vOWWW1BoqBVGVsqFfH24YZyuNhvYSCwTgf5vP/qd5eXlm268qVqrzofMq8oxxW3LZDuPaIcWhazURC+odIU+PtE83/vSV75cqlRuM/zNkaARs37whUdbchUnjKhMh2UTzWNHOL2HnNVrSCPJSoI/orw57CzXTja31tH06hsZVqnhBd7HPvaxBx98kBurzUI1q+kdzOcZ2lHHVkvsrcduQf/o//zXr5ubu3yHCtO1qFn3nBnP2++oab/xXDv7df2tYjpOr1SamfLL3/j5/2Ef259XVxfjE/WaDrmyjDerzKnLLilfddXCVa+b23vJv3jX+9TOHWquopprD/5fv3K6tnLVm6+75sY3g4+uGnYaO4aF0p6TbrN6t708k7aEJEet1apRljq+98WvfJmI+m0/elvLZyLa1/aZuGJ5lx9F1jKJvhqG8JbRVyyt0JLHsj8EXvfC2+n0aR12CIPQD7QRaF/m9m7L71wc40kvDb3Z0hiwAdgn7akQx2MRCKvpfXqW+dLTC4qN21oKtTtiYhiMLRHKgzCoqpQqdkZyL+XjPae2lgzbRHXmZ0KmnRL9OqOs2WzWm828+TVq7ZArqhDqkQvq0UM6cqVdc52f3j6uXa2N8LfFL5Pbck17SIVyYYqNiFTyfd/3fbt376b7pa7coTcCKtemyipaUotHa+rU9I7innd94K/sLGOvTrFJUOg0VVpR7OtKqLCwBwJN/21dx1BHnGO1Gqvl6BsrJ/ap5Ap/ejq41Heyy6+6fO8tNxXeeoN64+vVvj1qblrPfajR3UG+2YhiulbxV+OsymZGTAnUrrCrzZGBBgWko5ZULef22GGRlivWJhu5QrSQc4OrxoKzTitsXdVU5pOMyFAKf3ukR4m+asHdA0pL/s0Pm05f+cxSgnL6p/S/ONIZsb0e3HZiF1b+tHdipp8hhQ7LEPNMtqfcXwIaVs89i/TqfRpGZ2Ies7v6bx7jlWF9EMIqWi8wRarZhCQIY1KG7/oMPo2x9P6sYgedpi935ubZcaZmWueyFzBUkxFoJOSDSsyYxJUzPf0UnvsKcuV05SphqiX7bkNygQ5Hd5xJ59GShGw0PJ20K58tb8mMM9FpIM/2DqoKlv3Yj/3Yr//6r3srU2v1Fb+uKlPq9GGlXlHff+DGO96GWapop0YbBeZus60dE7v1rkExe7yOYpmOZum0E8wEabJ6PHrPW1aZO/jaK3dd/po9P/QuNVVS09OqPK0KbK3HxLwiljk+fTRyslqBvoUfXrZrbmelrtzj1ZOXlGfDxA2wTPQSredkxC/uvBZRYzb+lEUaf1q9dmkxjkauiFgwkcRaJnxaRPGijzOJvrK83zL6ykeBUSU2PkGvIWqIvfWPsAQx2tbMhMYMUGHP3GnV8fhbQDtHK+7tb2f8LQQFhgcYj9VhNJOYi0ZbyTf19EFs3e0FrbVMghhIwgDwqgUuMLW+9UNufyxENpqnCzEjMaGr99ImmsevdGxhHP0JRuSsi5kbLSNnrHsYHblyAxgZ6PnQBjRkzNTN9rttNXnfxWhldN17I9BgYvrzjbRJv6HarNK/mSpNzU/P/92//XdnZ2f//q9+or6ywpzweE41T6uZwvxffd9f/Yf/3c/o7ergtI64xYp5l5CBd4Lj5LfC2uukKlBsDKviku/t3/uP/uB3VHVVFV1VJJBJPwK/nz9hxqaxej0T8uUHu+dpjNR9STVPVFcW11ZYUTVbXuCKb4HSJBnaDEC5y5veoUJTZsGwcoUZgC+WQRBFHTo+U+vqOtE5j9tM8xN9NRQ5q57sz4ZD9sKm01dDmz0aBKVmIgsIJb1PK4dDAcn7BzwS7BDaFh8Fz5Ti7DzyvMvVLfKs1EIi5S07mKUwYIh8LWVJJiNyWpNpC3ERk11oAuNgH9MhLiIlA4tGrugMdeSqZT0G3np+F/tqbNlVNP2GuQIz3LrpYx/5Gz/+4z/OxO6f//mfrxQqn/iPn7j66qt3VHbwSFLWnpGT8fanuZYMoIC1u9RtMjZnfZvNElFhxr6OoegLRCPwpCvhSiUwIsEApFNWO3ZrZ3CFjcsrepmUdjcyh8VWrlpt8gInBKhkBXtBFeeX/HK9dKkqtoSfTCm8W74u1RClT/JORq70e0OQK5iYd3Gj5i/6qoXYVtFXZ4r5qOIg9wsCmxyBucpceGXITJ+5ubnrrruuFOjV5UzzGXV8i/BgwKw7680b7cD8SOa2MghDOEw3M/zB1iQ2HBDCg8Z+uV59ZSkMmQ2ogiJbEV04S7PJ+Sbkb3EEJq7vs8XxlupNHgIlv8RSuX379lmzBIGYmVHJ1CPM7JASx9WVleVTp9aWlmIWFGd6NRabNRxZOaUHvUKPIaussfZ//8avLR4/rOcwBCqdLla9jPkzfPQaPUmCgCBgxnIFBkFg+yKgB05Uyqpb5v2vNdbsFAkGDkdFpFar2T1TytPTM/PzldlZn0wcpxRFDEzNRsZ1Yk1U5DiFSjlx/vNv/NYrjz7B5ndlLywrh/KIUGPZRi1X7hcEtiQCEs3bkmyVSq0XAQZQ9cdhwmDGKKZ97DxGVZmb0xmSxGH65je/+eUvf/mRRx55k1s8sH9/Um8S6zt9/BR7XrzmsgMv3X3PqcXFk5des3fhcpYaMN2ScSY+Fcdn81hJgoAgIJZJZGC7I4AdYr8MFsx1lqOxFEEvmBsxsd+wXnLkujhMt77rXUymOHz48PWLOEoqbjTjZlScnlP1xv333n/Jjp0333DTG19/rcJf0vMmuIOdzDPzAvYRS5XbBYGtiMDIzW8rgiB12tYIMOuMSXTM+7fTGgnoMf/TL43cNJi1xisveNZzXOKBu/bu5aOn4cUx89n84yd4qTtAP/+1vwgP7r39Fz+mdu/W8yCYXadHex2W6YXFCzbVbltzXCo/+QiM3Pwmv0pCoSCwfgTsnh2MM7FGh+nanl405JZLoy1aorilpaWpcoUFd3wUPlfEnqssUA1UdUlNTWnzEzp6DySlrrz5+2+6/XY9sZxJ4816g12apioxLxP0PaaRt148s/4KyJ2CwFZEQCzTVuSq1GndCDADgjU6RPMYagp9s04uiQqePhkpsWi3M87E+lm/vRhczbD7PBuDN9V02WwopG56z7tUxHqmkjZOBZbd6kW9xPNcN2Ain1imkWCXm7cqAjJrfKtyVuo1IQjY7RPSp7/17bWXXtY04ZC1p0vorVVMPI8jnUTpJ04Iz4SMi46AWKaLzgIhYEsjwG57UfZH//4//NL//I+/+F/uVEtV1UzV6VW9jaz5eLxPnbnjqaqkarp3a6UtjYpUThA4NwLSSzs3PvKrILAxBMzshrjgVXbP7z14uY7pscdcie30TLYE9OzHFsK5JEFAEJD4gciAIJArAqei0ztmd3zw73/sbR/98Ut2X8p+EI2sGYR6h3Cmi1sfqXers3zf7pVrVSVzQWB8CEg0b3xYSk6CQB8C07NzzG5gy7zdu/dystxcXVxdsWaJe2l+fDpDTZxIEgQEARCQaJ6IgSCQIwJB5DSOH2eDieKuXSqJw2BKlVxGnsyW5KZc6zG1j8nIswJzJF6yFgQuFgLiM10s5KXcbYHA0Qe/9fwjjxWZMM6b9k6vqGUW3uI61VozIIju2T1fObHn2wIVqaQg8CoIiGV6FYDkZ0GgF4He+QpE5zof6/OcfuWoNjzMvjuxwjKl3/rn/1p99k9eX1/++PveufbAV9QuT82731v7XnWhVC/5zZLLW6D0+7xYxMSH85EX+PaSJueCwNZBQKJ5W4eXUpOLiEAzaoZ+YcfCgtncweUVgs8+8MC111675/or1anjbGj+0ksvvX71DWrGLwZ6da1NnRP9lCRBQBBoI9BtGu0r8lcQEASGIjCswbDtHju6Kt9fOX6ch5Ms/fwXvnDjzW9RYSn79neb1eZUWFKux2dmapqNJ7BEZ2fV644NLV9+EAS2BQJnt45tUWmppCCwAQRoM9bD6W08rReQO8q+SoPdXRcWFoI9e9Ra9c8//xeB5132mitUoaxSN3ADHmcanrZEvRPGN0CSPCoIbDEEJJq3xRgq1ckXAcwJ1gSbZGd+d4wTO+/hEPGb3kCP9zwVww9+6K9oUk4tfe97L7/hmjeofftVlKqkUVNZaWqeX/Sz1jIZQ6dfeitJEBAEDAKdliV4CAKCwLoQ0L6OsStnmBJ2dnCwOw3Fq2zjSBWCkJdcVKsnPvfnK8ur77/9x1SZHccLyg+dWDtMNLyzHCZMnV14uy4i5CZBYEsjIJZpS7NXKjd2BPByekJwHePEKBNFab+HT9EsSnJUs7r2X/74j8NSef49P6KN0alF5QaVyrRKeYfuGflYMnsyHjvdkqEgsJkQEMu0mbgltE4KAqyUteG4NkEx77lg4TovZIpYoETKTrzwfJwm1UZy8OprVbmsjp948O5v6E3zvOCMZbZtE8Vf8ZkMdHIQBEysW2AQBASB9SLQNiTWc9JBOfNk62WDvG29EMRra7yiaecVV/y7X//3Dd9927t/UPE+wpXq4ura6tFjWLRDh185uziTi/hMZ8Mi37crAuIzbVfOS73PDwFrmYwNsTbJZsP7cO2sPL7yanXsVVZda0TRzgMHZn78x1WUfOpP/njf5ZdPXbI3ipr7Lt17foXLU4LANkFALNM2YbRUc0wIdCyTPWnn6vlBqjLsk7ZJfOr1RGUHr3rtiaiu1lYWH38sKvjXvuUmnKeXXzmi5/X1mrV2Jsw5b5/KX0FgWyMglmlbs18qf54IGJ+JZ7EvnSbEkqZqtcpFbBIrbf2pqXe/54dvfPe7777zMyfqtQ//wt9QU2UM0o5LLqnHA02QmKXz5IY8tvUQkPVMW4+nUqM8EcAmW
Xenc9IuzVGODej5xTCtNbi858CBPX/v7xx64IFLr7la7ZyPVbbabBSKIcZMmzbyaVs4ThxeldHOSv4KAtscAbFM21wApPqjI9Brk9rn9Ua9GBb9QqCzc5wUM4PhaTQJ3136tluUz5Q8tZYkXqHIJrDM3rPGCWukvSdr6kYnRJ4QBLYqAtJL26qclXrlg0DHyyH79jmtiH3zuOB5njUzerOiNG00G/WjR+ybAY8vLfp+ETOEM7W81mg/2iWSTGScqQuHnG1vBMQybW/+S+03jIB1eIps/cAIU5IsLy9z4mKiPDecni5etk9FhPGS2TmiedpBYgOI2crA9wPKONOGmSEZbBUEJJr3apzsjbT0nut4DB8AzFQWoHoUb4eTkYJXg3PyfodrnuEgJ3ATHvf4M2dw3NBeGFAD7go93ZSmK1Otn4P2m9O9UBW0HeK5sx/lMT7tzqGjfJ5BjCQJAuePQK/E9p5vNn3Vbhbnj4Q8KQgIAoKAICAIjBMBsUzjRFPyEgQEAUFAENg4AmKZNo6h5CAICAKCgCAwTgTEMo0TTclLEBAEBAFBYOMIiGXaOIaSgyAgCAgCgsA4ERDLNE40JS9BQBAQBASBjSMglmnjGEoOgoAgIAgIAuNEYKhlYgcwlrUnZn0FG4KNs8zzystz9QIRltYXCoUG77Rm9ZBvdoI5r9zG8lDAK+BY0h81IEmv+dfrYtqrWMZSwHllYpkF42Bf570M55VTLg9NnFwZlrXkKjJyZdiaS+XXl6kVbIS8K1dG+Nf3dF53iVyNhKzoq3XCNUyu/MzsqpKYrfs5st8XHxIahOZqVS17+3uZg6ZD+zpBvotzoWFgghgIqNVqvPyGlfb2niRlT+eedZEDn9zYRf1W7Hayby6wx9R1PEfbIYip1+sQ1kybvutjDtq35/I3dnxLUmYIAy030yU20zoXvMCNncx1WbPpgZg1A7nQcb6ZniFXaZRlThKlkFzgnUaZm/LKV2TPyEBLEjK9609+KfXdOO2RK9Pb0XKVZVraLch9MpAjPciVsUNduYqayDy4DSzUisHAn8ZykRd7kA+tnnd8uD7rh9typWLbUpE+aHANdSA2rP2OhRgy8QwvKIVmyFH01VnAbhl95TtoBNa+w2mzIB0Bsy0giiIkL1WpywuiMVGO55k783afrLifBTdf0yxlU7IgCMIwpC9pb3AcyM/Z
TenRSrbu9kLUwklBDCRhnKxC0W+NyzlZiGwT1UVpFapCV++Ok9GjUAmbUqAutM9k32Knb5qUhFxBbkeufIwp73s1VYB6z9RN74VqpJGjr/dlyDHBRxjXL1dc1JbJltwnA/kRFJl+Bvl35YqNjsDB7DHRX27O0o8pMPg7ijfHd+RK06N1hk7ABA2mR6G/tq7q03yS4YXoq6Hg9snqJtVXvlZlaArTB9EdEK01/v/2zrVHjuIKw32d6+JLJLBQ4E8ggWMQQogPiWLJvyx/BkfrOCFICZhgY5DIB2RFXCREjGQcG5vdufYt76nT01O7U212vdN0L35bZqit6e069Zy3zqmq7p2R4/z589MJvpRzsUiy2A+iwchUy1pKCw296nx58+KTyWQ0Go3HY7zi3TSTrSrMK0Pz0S+b52+rpm4Ogg/rlI/vlPDlwSSkARQms0m/P95W087rYFVhT+QRHUoLxRA5sAuUYA82ChHahuNx0/7SRo/+Cl3NoKtssUiz2IP3Sl2JDougXI+amKdKwIzk6Bd/ijMniwm+KH2tKyzRMmxkZ5ht4Go2ar24WvgUDR3xV1RXmAvi/LWuJhNY6LyCrU/nCSesDFY5R3RV5L7RFYzB3EIzkypQ10wo143fE5pR/XpgAi1agSPwynhVkdGCrQfVqr6eungV/eXaNXRpc3W8t7f33+++++yzz/Z/fIzpOT7fH9JczufxUObmzR11uwFIQhcuXLhz587Ozs7HH3+M3TPEXNmwWuIrBRo86jwd9GIJ+mEwHA6/+OKL/f3925/evnfv3qhodhab+rGaZNZMojrdzZsu9/uDQW8Qz9JlFhQ7585+++23v3355WvGvw0COualoau7qqtHj8PcH0a95TxZzJYjfCLqejdPgp4qISqa9e/UP6wrZKbQD3Rtp6g3NXDMTh/jdNUVhL3W1W3RlUyDXMd66ex69+R1yWyOD6vFN04tkiU88pzR1cvQ1fVr4iSsmTAIOrCbx3ilvt7UqmamUxevyv3r9RzEzETQSclDyyXGJ1ICblJh212PpufgdXMumKEGoACrYBuMfML+u/rp5K91nsYcX7bLsDgx970q2/LVDtDJm3ZeIcdX/5hpo3k1qjOritI9RQEH4eabIoITm/aX08gnVB7QFRZJq0PsxF6kiXa5fG3RqtzwmgmPilS+U2iYlfthOS4s1GWfdJw/oYMnfcvoChc5pCtsXDuvbOvTecIJK1f+MbrC18mboae6UoN8KB6CXK1s68bvCc2ofl37y3hVATlUsPWgWi0Ve9riVXT5yhXpm7nPhOcKqtXxN998c+7s2bfffBufoo05UWTu9uuZh1hs98e6z1rGUxh4ZunmzZvYSXjrrbcwUPWIGs4Ecv+tOsxY1Ap8sQG23fG92ji++uZrbDZeevVSUiQ7frNPDGLTUCPCerKsBpn9FMT2JZ7JEKPDm5/c6g0GV9S/VRfaLvz77n/OQ1dvvI1FEb7LqCe3ltb3mbRvOpZUCc3eZfK8/SKJ/fjmK2tdwSrcW8VsrJX7TKKr1fH110ZXv7uk4ne6zr2Scp76dJWqLnOfSaaofvjxJ7ewirryxyulDiG11bantKC1T9fWUX5rZQ/+z3jlAKZ89A3jC604dfEKD0SJ5fgP4UBezT/U3L17dzQcooBnH/IsWaYpJnH41hmMGu11Q69lht+4OtISnpi6f//+dDrFlG08Krfdm7bnwBzEWKUWyiA1oxA3KmAVMhNm34hxTdtToFnjAfWDaG/lEFlNZssCXgoiDFqAuv/gQdP2bDjqZyqgq7HqCvtAebpI0zjs4Xkvk+jLqKYdUs5N2w+XwXFrXQ3GmpAw7RAzjCmbGviZTp7gbZ1vQVmT6UpXeQbxwx7nVRsejjAEz8BliyyVRwajGDNX6OoBdLWyB2bhX4XIbaXT9Keq1IakUcYrF8DKEXhTfXFK4xWWHBIOzIsEWv2HmnPnzuEBA+27yUll1MDI0cqGXuuujrQkQyOKYIA+BKETyabtWQ1A6e5B2/IkS7D7Pxr0/CBF6Ag97O0lvt/sfTjYUDnrkAtgTBD2MTnSnRWwghMb53PIiJ/7ESYVla6CKOqhN0hLB3pld7Bp+zNvjudY4D44Ea7EszXYv+6FfTPzOORx6VvD8pcmVNgQOfoOJ8KpKn55b+No3B64Jgz7EW4nHdTVioQIElatxkbj9hgClULK1hmvKmFoOlJKVaUUTlm8Wj3RdaAP/IEESIAESIAEWiPAzNQaejZMAiRAAiTgJMDM5MTCShIgARIggdYIMDO1hp4NkwAJkAAJOAkwMzmxsJIESIAESKA1AsxMraFnwyRAAiRAAk4CzExOLKwkARIgARJojQAzU2vo2TAJkAAJkICTADOTEwsrSYAESIAEWiPAzNQaejZMAiRAAiTgJMDM5MTCShIgARIggdYIMDO1hp4NkwAJkAAJOAkwMzmxsJIESIAESKA1AsxMraFnwyRAAiRAAk4CzExOLKwkARIgARJojQAzU2vo2TAJkAAJkICTADOTEwsrSYAESIAEWiPAzNQaejZMAiRAAiTgJMDM5MTCShIgARIggdYIMDO1hp4NkwAJkAAJOAkwMzmxsJIESIAESKA1AsxMraFnwyRAAiRAAk4CzExOLKwkARIgARJojQAzU2vo2TAJkAAJkICTADOTEwsrSYAESIAEWiPAzNQaejZMAiRAAiTgJMDM5MTCShIgARIggdYIMDO1hp4NkwAJkAAJOAkwMzmxsJIESIAESKA1AsxMraFnwyRAAiRAAk4CzExOLKwkARIgARJojUDUWsunpWHfMtQue0jq+AeAhVfEXpF5XmxqrPNZPAUE4LXQeBAFeBM+LtZWH/D4upolEugoAVuxdvm0xSuumToqMJpFAiRAAs8sAWamZ9b17DgJkAAJdJQAM1NHHUOzSIAESOCZJcDM9My6nh0nARIggY4SYGbqqGNoFgmQAAk8swSYmZ5Z17PjJEACJNBRAsxMHXUMzSIBEiCBZ5ZA5OU5Op/7XuHLK36Qn/E3HUWRZVnu5aEX+PJHHnLkSeJFoZYbeoUNziMMQvzdUJIkw+FwuVz2e/04irM8q2xz/tbJK33rj1uACIe+ZvgTmDAGq2W69H0fhsG80Atzw/Pk7dZdIfcDNal8xR/gGAvTLIli/EUOXAUrCzgO7guDoGl76uysq3fqKk2SKMQfFQXKVjVQvqIrTR4HdJUu+1EfbhVd+eJsG7VaoRY2Z5HoKhI/QuRrXQVhXsNBLWzOHi/NgrWuEBxEVwF0JdFCDrzCBvys5brxK29v4wiM2tEKHIFXNKv6cOqK8QrIT2m8irxAlk1IPvC4FYRFRDo4syIr8iIOoiLPoUg9X95u5jhkQ9VIkiZoPY7jMFxHf1gY+A0v+yyDTLAqKZlBIdYh9MMkGIaxivDRDySsNHegt2qGDlFpyFgYFJKEACMtUhMdwEZCh7isY0epKy8rCi/0I5hd6qpYdc3EPAXftH+TIkETTl1VqO2BofCbI+qvMtBaVyjluaarzXYxcps9oDNMtsIgzdJc5qgrXUnMkAOUpHqlssbtUbUzXtV5/dcSr6J0sUAfsfRAasWrTEOM4qIowowbiSj08R/WAxCfqG9hzq/DcvJ62OA8EP0xvcWCCQfiiJ6DmNK0PfacVGcf+hr1+moDjIFJskDxwsIvmrYn9WM1CT7R+VBgYlk0lLUsokjow2Ny9Ho95KWm7TFNHeMFujLZMoC5GsVEZX4gOkRyNREuN+FflZAVyTGufvxT/T4Way5dLReSmcw439TA8ds56m9E/Q1dYfgVxWIp43TzMDLYrN5aDTYn9FoYf0hAWKBAV3DZIluozEKkrdWaCcTqxu+2DNL+ohXGKyfSTa2e0ngV6UiIzBwEH7BTrY4fPHiAzIQZJSZM+TJBOMFkqSenl0p1cjl5JWxwHtPZNPGTx48fp2m6t7c3Go0wVDBiBw3bY8+XdVNTJyXzLAGQJM+m0+mjR48mk8ksmcGecX/ktH9blQjoZUSoJkfYRITjsiRJ09zLEi8P+hEwCqs8b9pfx+0XdBVBV14iSluksazBwzjsiQ7RI9M3HUuqhMhrVm/T5WFdxUiaeYGILJlJu1ehxo9l1XH7fdTz56noChOdta7moqvR0K0r8X2jB9ZKOPDpW0Ue9GJMW6ErrOH6Yb/UIRI7qKwQIZI0e5iGGK9qIa8cIScYX2jFqYtXkWzFutZMZ86cQWaKfeyeYUpZztNxJm6oSJ8bO+rmXDoykZDG4/HZs2erTZ6m7amGHHqsEVNfdXclCKL4TAyTEDuG8RDnNG1PtWbKRXFii66ZAoQKpGovx3IS9yoQVeFBZKam7TmuEGAVMlPsxQhnYb8nQQ0bQlgtQVeuNVPR8Jpp1JOIX+rqzFndrcbKTXaPVwF3UwPH7fXRz9f9gCjETcOVrgZGV6l73BkZHP3yxz4TOsctQDsTwIPITJizag6SmWsH1kyMV+raTa2e0ngV6e1N7Ksg0GEoVmsmzLUX8zn0h4l4gClkGMvMKc97IxknzR2wwXnoTWkMCUwn5/M5xi3KMOnMaOw8f2uVNXOQn2YT2ZgKA4R+mARjzAgt+qudxq0ZcPBCCAcaEcy2himaNdN8NsF2axgHmBzhqZUiCGBVfzDQSHfwGm3+BF0toStEftxeyrwBHjfAwyMoDIeQoO7v6VhSJUTyObkNHlPZf/JLXS1EVx6klqTj0Vgyk7a8oYHmDPppKrrCdtlaV7jNW5SPRWy22/SaaTmdwRg/jpZpIveZQtHVALrCrrKxRmauqxSOCvXgpp1bqzG+YLyq5bmhVa04dfEq2r16FZ3c3Lf9/vvvf7h378aNG/O9CYLguD/E6MXjerNkWQtlG2/UrZkwOF944YUvv/xyZ2fn008/nc1mGCHY98BO4zaarb1G3RwEOxswyY/kFsVXX321v79/6/atH374YVDXgdoWjvdGtWYymWm9ZooGyEu4x+TtL2ZZUAx2xnfu3Hn+woWrxr/Ha6PJs6Gr+9DVRzfm+5Mw93f6Q6SlHI9tLJfONVPU8JppHh7WVYGn0Tx52FIykxnWmxpojpDqCjvVa13dEl1B6s5GjQyc72ynchj3ZNs8DKbzGaQ9NLq6AF1du1pmpm7cZ2K8Un9varWc5522eIWVupl1mTuKmCJC/zoEXnzxxdl0imyEmBt5Pm7uy9gwz6FtR/J1V3EPQA+D8/nnnz9//jwyEyZx2IWXNUEfz/g2O2us8zTWkni4AJkJW3mwCnNtJKqHDx++/JsX6nq2lfoCDziYcGllJkGW4v4EvJVkk+kk9WVp+9xzz8GJpX+30vY2LgKT5pWuCjzxiZ2zEMlJ7CxwL1NWSmUUNkoIV8+qbaNxxzUePjysK2SmQQ87o2ErmUl1hdYP6QrTMof12BG158jOM05WiW0JyCpNCtxJxd2mvqWrMjNhHbVa7Brnnay9n/vtsr+MVzWgfjXxKvrD5cvSx40nID7//POXXnrpnbfeQeCX+wCaec2ZNUy2U133BAS2WPBs3vXr17GT8MYbbyCB4k4ANsGbzUvoE/Y3q8OMRSWBiX6SJYggeGzxnzfe7/X911979eJrr4y8QXV6E4VUfCXHOiRpbDJ/UYL7TAgfMBkYb/zrI4SVy+rfJkx5qmt++Kfboqs3VVf4QiTMd0RfcjF05ABhqWv6C8Sm3hzbUdf/+mfR1aWL0BVmPL1QHruoMpMYVh3G0uqnrRfgOBU2dPXBBx/gQbjXL71+8eJFiN/ZlrvWeerTVWrf5Y8koCt5Nu9D1dXvL5c6lK+3Wj8BUarz6do6ym+t7MH/waq6+8B4VcL7tcSrhsfZUaTGc0iABEiABEjAIsDMZMFgkQRIgARIoAMEmJk64ASaQAIkQAIkYBFgZrJgsEgCJEACJNABAsxMHXACTSABEiABErAIMDNZMFgkARIgARLoAAFmpg44gSaQAAmQAAlYBJiZLBgskgAJkAAJdIAAM1MHnEATSIAESIAELALMTBYMFkmABEiABDpAgJmpA06g
CSRAAiRAAhYBZiYLBoskQAIkQAIdIMDM1AEn0AQSIAESIAGLADOTBYNFEiABEiCBDhBgZuqAE2gCCZAACZCARYCZyYLBIgmQAAmQQAcIMDN1wAk0gQRIgARIwCLAzGTBYJEESIAESKADBJiZOuAEmkACJEACJGARYGayYLBIAiRAAiTQAQLMTB1wAk0gARIgARKwCDAzWTBYJAESIAES6AABZqYOOIEmkAAJkAAJWASYmSwYLJIACZAACXSAADNTB5xAE0iABEiABCwCzEwWDBZJgARIgAQ6QICZqQNOoAkkQAIkQAIWAWYmCwaLJEACJEACHSDAzNQBJ9AEEiABEiABiwAzkwWDRRIgARIggQ4QYGbqgBNoAgmQAAmQgEWAmcmCwSIJkAAJkEAHCDAzdcAJNIEESIAESMAiwMxkwWCRBEiABEigAwSYmTrgBJpAAiRAAiRgEWBmsmCwSAIkQAIk0AECzEwdcAJNIAESIAESsAgwM1kwWCQBEiABEugAAWamDjiBJpAACZAACVgEmJksGCySAAmQAAl0gAAzUwecQBNIgARIgAQsAsxMFgwWSYAESIAEOkCAmakDTqAJJEACJEACFgFmJgsGiyRAAiRAAh0gwMzUASfQBBIgARIgAYsAM5MFg0USIAESIIEOEGBm6oATaAIJkAAJkIBFINq9tmv9uC7O//coy7IP3ntvOp0OBoPZbIZX1KzP+GVLQRDkeT7b28+Xye67V3u9XlEUsAf1v6whZWswJgxD3/eXOB7Ok8Xi77t/UyNbsQeNwp75fD4cDvE6Go2SexPU7O66/duWkdm9Cbz20Xv/6JSukh8XQd+7/u61Tulq+tPeYrG4vrvbKV0hMkBX73dMV4xXTx7Rpy5etRPWnwyR75IACZAACTzLBP4Px47KfH71UYkAAAAASUVORK5CYII=" alt="" width="343">
如果一个图形变化了,那么这个j 和i向量就不在是以前相互垂直90度了,然后里面所有的点坐标可能就位移了。
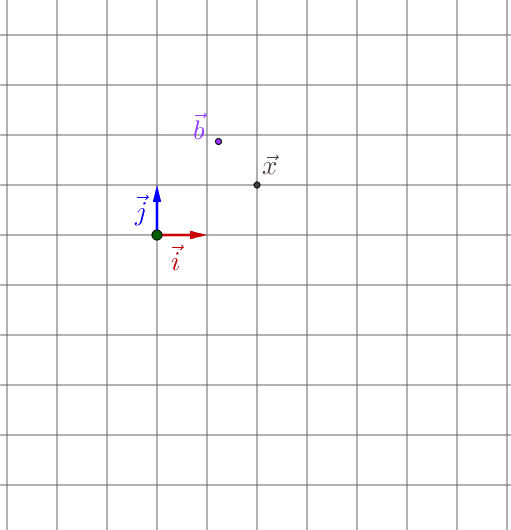
比如我要把x点移动到b点怎么实现呢?
我们可以把上面的直角坐标系想象成一辆公交车,所有的点都坐在公交车里面,我们在车里没有动,然后公交车到达目的地后,我们相对于城市而言已经走了很远很远了。
就像这样,x点是不是就移动到b点了。
重点:所以计算的思路就是,通过老的直角坐标系的规律获取到每一个点的位置,再找出新的坐标系的规律,把点移动上去,就完成了第一张图片所达到的效果了
下面开始找规律
假如新的图片变成了这样
由于4个顶点已知,那么这4条边有多长,每个边上面的点的具体坐标我们就可以确认下来。
由上下两条边线确认两个顶点,我们就可以确认某一个X坐标上面y的线性变化规律。 比如以前图片位于x方面1/4位置的坐标点y方向线性变换在新图中的线性变换就变成了左图y’. X坐标固定,这时候我们只需要传入以前坐标中的y值,就能得到相对于自己宽度1/4出的新图中所有的坐标点。

同理可得,以前2/4 3/4等等所有顶点方向的y线性变换规律我们都可以得到。
然后我们要做的就是通过
循环遍历出所有向下顶点然后得到第n个位置处的所有y方向的点,从而得出所有的坐标。然后这一组坐标的就组成了新的图片。
最后附上关键代码
//数组包含了一次是 左上 右上 右下 左下 4个点位置不同,图片显示的就不同
1 -(void)changeImageByPoints:(NSArray *)pointArray{
2 UIImage * image = _image; //全局需要变换的图片
3 float width = CGImageGetWidth(image.CGImage);
4 float height = CGImageGetHeight(image.CGImage);
5
6 CGPoint p0 = [pointArray[0]CGPointValue];
7 CGPoint p1 = [pointArray[1]CGPointValue];
8 CGPoint p2 = [pointArray[2]CGPointValue];
9 CGPoint p3 = [pointArray[3]CGPointValue];
10
11 //痛觉相对于父视图的绝对4个顶点计算出新的宽度和高度
12 float minLeft = MIN(MIN(p0.x, p1.x), MIN(p2.x, p3.x));
13 float minTop = MIN(MIN(p0.y, p1.y), MIN(p2.y, p3.y));
14 float shapW = KINT((MAX(MAX(p0.x, p1.x), MAX(p2.x, p3.x)) - minLeft));
15 float shapH = KINT((MAX(MAX(p0.y, p1.y), MAX(p2.y, p3.y)) - minTop));
16
17 //change point relative to image not superview
18 p0.x = p0.x - minLeft;
19 p1.x = p1.x - minLeft;
20 p2.x = p2.x - minLeft;
21 p3.x = p3.x - minLeft;
22 p0.y = p0.y - minTop;
23 p1.y = p1.y - minTop;
24 p2.y = p2.y - minTop;
25 p3.y = p3.y - minTop;
26
27 //创建一个bitmapcontext
28 if (!_first) {
29 needData = malloc(KINT(width)* KINT(height) * 4);
30 CGContextRef imageContext = CGBitmapContextCreate(needData, width, height, 8, width * 4, CGImageGetColorSpace(image.CGImage), CGImageGetAlphaInfo(image.CGImage));
31 CGContextDrawImage(imageContext, CGRectMake(0, 0, width, height), image.CGImage);
32 data = malloc(KINT(width) * KINT(height) * 4);
33 data = CGBitmapContextGetData(imageContext);
34 _first = YES;
35 }
36
37 //初始化新的图片需要的data
38 unsigned char* shapeData = malloc(shapW * shapH * 4);
39 for (int i = 0; i < shapH -1; i ++) {
40 for (int j = 0; j < shapW -1; j++) {
41 int offset = (i * shapW + j) * 4;
42 shapeData[offset] = 255;
43 shapeData[offset + 1] = 255;
44 shapeData[offset + 2] = 255;
45 shapeData[offset + 3] = 255;
46 }
47 }
48
49 //给data添加对应的像素值
50 for (int i = 0; i < height -1; i++) {
51 for (int j = 0; j < width -1; j++) {
52 CGPoint originPoint = CGPointMake(j, i);
53 int originOffset = (i * width + j) * 4;
54 // 计算原图每个点在新图中的位置
55 float xFunc = (float)originPoint.x / (float)width;
56 float yFunc = (float)originPoint.y / (float)height;
57
58 float delx = (p1.x - p0.x) * xFunc;
59 float dely = (p1.y - p0.y) * xFunc;
60 CGPoint topPoint = CGPointMake(p0.x + delx, p0.y + dely);
61
62 delx = (p2.x - p3.x) * xFunc;
63 dely = (p2.y - p3.y) * xFunc;
64 CGPoint bottomPoint = CGPointMake(p3.x + delx, p3.y + dely);
65
66 delx = (bottomPoint.x - topPoint.x) * yFunc;
67 dely = (bottomPoint.y - topPoint.y) * yFunc;
68
69 CGPoint newPoint = CGPointMake(topPoint.x + delx, topPoint.y + dely);
70
71 int newOffset = ((KINT(newPoint.y) * shapW + KINT(newPoint.x))) * 4;
72
73 //give shapeView new value
74 shapeData[newOffset] = data[originOffset];
75 shapeData[newOffset + 1] = data[originOffset + 1];
76 shapeData[newOffset + 2] = data[originOffset + 2];
77 shapeData[newOffset + 3] = data[originOffset + 3];
78
79 }
80 }
81 //创建新图片
82 CGContextRef newContext = CGBitmapContextCreate(shapeData, shapW, shapH, 8, shapW * 4, CGImageGetColorSpace(image.CGImage), CGImageGetAlphaInfo(image.CGImage));
83
84 CGImageRef cgImage = CGBitmapContextCreateImage(newContext);
85 _imageView.image = [UIImage imageWithCGImage:cgImage ]; //这个_imageView就是贴上viewcontroller上面的UIImageview
86 _imageView.frame = CGRectMake(minLeft, minTop, shapW, shapH);
87 CGContextRelease(newContext);
88 CGImageRelease(cgImage);
89 free(shapeData);
90 }
 加载了一张image,根据四个顶点任意变换。
知识点:1.BitmapContext 2.矩阵变换
一.什么是BitmapContext
官方解释:
The number of components for each pixel in a bitmap graphics context is specified by a color space, defined by a CGColorSpaceRef. The bitmap graphics context specifies whether the bitmap should contain an alpha channel, and how the bitmap is generated.
通俗来讲:
首先,我们根据图片创建一个BitmapContext,把一张图片绘制到这个BitmapContext上。这时你可以把图片看成是由很多个彩色的点组成的。
加载了一张image,根据四个顶点任意变换。
知识点:1.BitmapContext 2.矩阵变换
一.什么是BitmapContext
官方解释:
The number of components for each pixel in a bitmap graphics context is specified by a color space, defined by a CGColorSpaceRef. The bitmap graphics context specifies whether the bitmap should contain an alpha channel, and how the bitmap is generated.
通俗来讲:
首先,我们根据图片创建一个BitmapContext,把一张图片绘制到这个BitmapContext上。这时你可以把图片看成是由很多个彩色的点组成的。
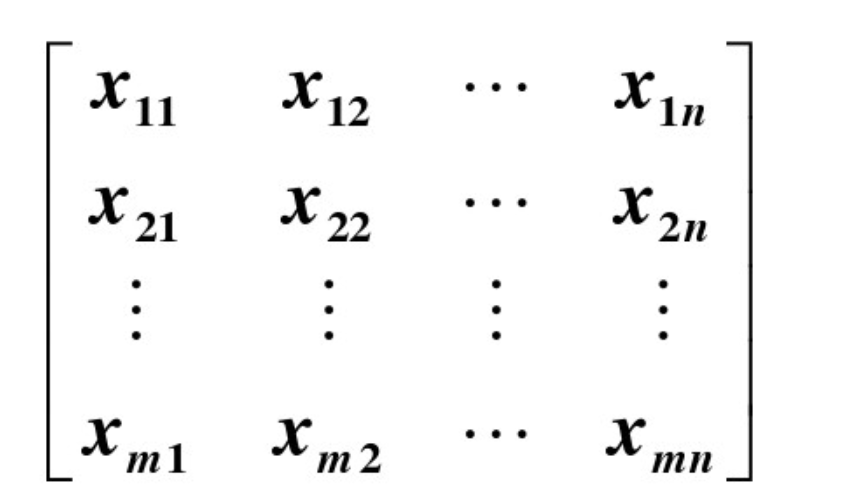
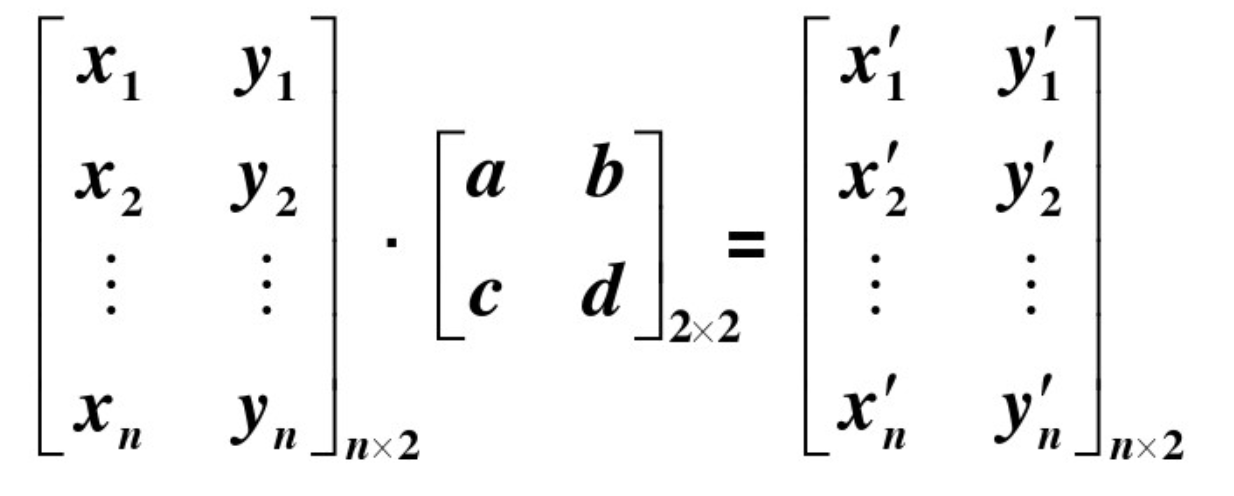
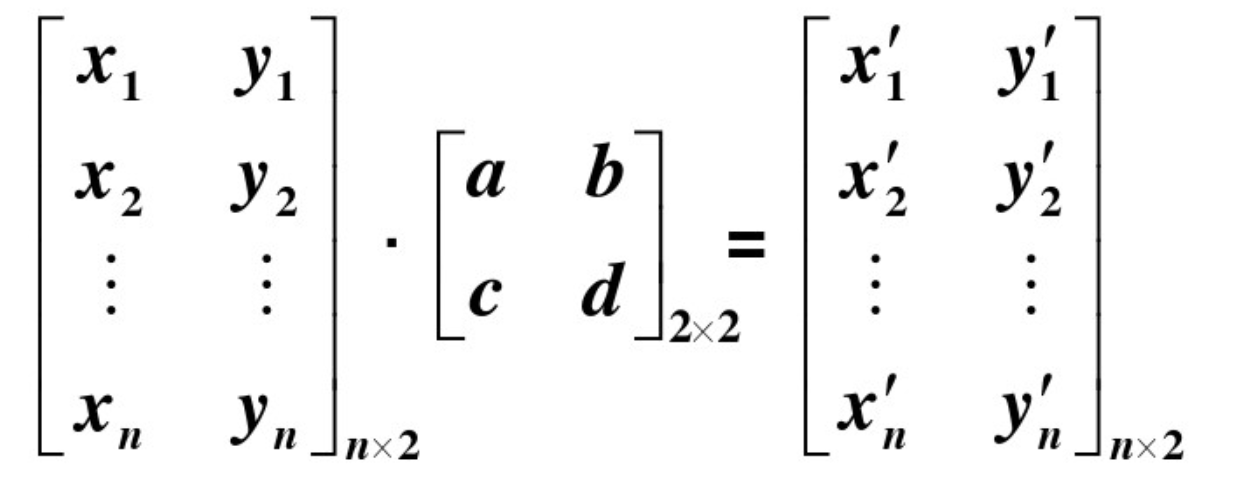 原始坐标和变换好后的四个顶点坐标我们都是已知的,可以通过已知数据建立一个4元一次方程式,得出a b c d四个位置数然后计算出新的图形坐标。此方式适用于做数学应用题。
方法2.通过x y的线性变换找出规律
我们之前拿到的图片都是很规规矩矩的,是一个矩形。加入得到x相对于自己图形空间的坐标的话,这个x的坐标就是 (7/11 * 图片宽度,4/8 *图片高度)
原始坐标和变换好后的四个顶点坐标我们都是已知的,可以通过已知数据建立一个4元一次方程式,得出a b c d四个位置数然后计算出新的图形坐标。此方式适用于做数学应用题。
方法2.通过x y的线性变换找出规律
我们之前拿到的图片都是很规规矩矩的,是一个矩形。加入得到x相对于自己图形空间的坐标的话,这个x的坐标就是 (7/11 * 图片宽度,4/8 *图片高度)
 比如我要把x点移动到b点怎么实现呢?
比如我要把x点移动到b点怎么实现呢?
 我们可以把上面的直角坐标系想象成一辆公交车,所有的点都坐在公交车里面,我们在车里没有动,然后公交车到达目的地后,我们相对于城市而言已经走了很远很远了。
我们可以把上面的直角坐标系想象成一辆公交车,所有的点都坐在公交车里面,我们在车里没有动,然后公交车到达目的地后,我们相对于城市而言已经走了很远很远了。
 就像这样,x点是不是就移动到b点了。
重点:所以计算的思路就是,通过老的直角坐标系的规律获取到每一个点的位置,再找出新的坐标系的规律,把点移动上去,就完成了第一张图片所达到的效果了
下面开始找规律
假如新的图片变成了这样
就像这样,x点是不是就移动到b点了。
重点:所以计算的思路就是,通过老的直角坐标系的规律获取到每一个点的位置,再找出新的坐标系的规律,把点移动上去,就完成了第一张图片所达到的效果了
下面开始找规律
假如新的图片变成了这样



 同理可得,以前2/4 3/4等等所有顶点方向的y线性变换规律我们都可以得到。
然后我们要做的就是通过循环遍历出所有向下顶点然后得到第n个位置处的所有y方向的点,从而得出所有的坐标。然后这一组坐标的就组成了新的图片。
最后附上关键代码
//数组包含了一次是 左上 右上 右下 左下 4个点位置不同,图片显示的就不同
同理可得,以前2/4 3/4等等所有顶点方向的y线性变换规律我们都可以得到。
然后我们要做的就是通过循环遍历出所有向下顶点然后得到第n个位置处的所有y方向的点,从而得出所有的坐标。然后这一组坐标的就组成了新的图片。
最后附上关键代码
//数组包含了一次是 左上 右上 右下 左下 4个点位置不同,图片显示的就不同