HDU 1410 PK武林盟主_C/C++_编程开发_程序员俱乐部

http://acm.hdu.edu.cn/showproblem.php?pid=1410
Problem Description
枫之羽认为自己很强，想当武林盟主，于是找现任武林盟主氢氧化铜挑战。氢氧化铜欣然接受了挑战，两人约好于下个月的月圆之夜在HDU校园内的三根柱子上进行决战。这场PK赛肯定能吸引武林中所有人前来观战，所以他们找了有商业运作潜力的经济人你，让你来组织这场百年一见的世纪之战，假设两人都有一定的血HP1、HP2.HP1是枫之羽的，HP2是氢氧化铜的。他们也有一定攻击力AP1、AP2，AP1是枫之羽的，AP2是氢氧化铜的。当进行攻击时，对方的HP减少自己的攻击力，比如HP1＝2 HP2＝1 AP1＝1 AP2＝1，当氢氧化铜攻击枫之羽时，枫之羽的HP＝2(原先的HP1)－1(氢氧化铜的AP2)＝1。现在两个人对决很多回合，每回合不是枫之羽攻击氢氧化铜，就是氢氧化铜攻击枫之羽。求枫之羽能赢氢氧化铜成为下任武林盟主的的胜率。

Input
该题含有多组测试数据,每行为HP1,HP2,AP1和AP2 (1<=HP1,HP2,AP1,AP2<=32767)

Output
每组数据输出一行，为枫之羽赢氢氧化铜概率的值 (结果保留4位小数).

Sample Input
2 1 1 1

Sample Output
75.0000

公式推导：
设：
枫之羽为x，氢氧化铜为y
x需要打n次才能打败y
y需要打k次才能打败x
一个回合中，x打y的概率 = y打x的概率 = 0.5
要x赢，则x必须打n次，而y可以打0次，1次，2次……k-1次，而且最后一次当然必须是x打的，所以（设y打i次），那么一共打n+i次，要在前n+i-1次选i次让x被y打

所以x赢的概率 =
C(n+0-1,0)*0.5^n + C(n+1-1,1)*0.5^(n+1) + …… + C(n+i-1,i)*0.5^(n+i)……

所以有公式：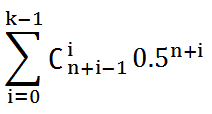

但是组合数会很大，怎么办……于是要用到取对数的方法
找规律：


设double型变量c，使c = lg(C(n+i-1, i))
不断递推出c

于是有以下代码：

#include <iostream>
#include <fstream>
#include <algorithm>
#include <string>
#include <set>
//#include <map>
#include <queue>
#include <utility>
#include <iomanip>
#include <stack>
#include <list>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <ctime>
#include <ctype.h>
using namespace std;
#define L __int64
#define M 1005
#define inf 0x3fffffff

int main()
{
	int h1, h2, a1, a2, n, k, i;
	double c, res;
	while (~scanf ("%d%d%d%d", &h1, &h2, &a1, &a2))
	{
		n = (h2 + a1 - 1) / a1;
		k = (h1 + a2 - 1) / a2;
		res = pow (0.5, n);
		c = 0;
		for (i = 1; i < k; i++)
		{
			c = c + log10 (n+i-1.0) - log10 (i+0.0);
			res += pow (10.0, c + (n+i)*log10(0.5));
		}
		printf ("%.4f\n", res*100);
	}
    return 0;
}

• 
• 大小: 1.9 KB

• 
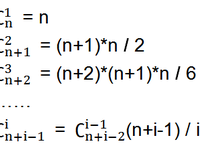
• 大小: 5 KB

• 查看图片附件