0.1 + 0.2 为啥不等于 0.3 ? (正确结果:0.30000000000000004)
0.8 * 7 为啥不等于 5.6 ? (正确结果:5.6000000000000005)
var_dump(intval(0.58 * 100));
正确结果是 57,而不是 58
其实这些结果都并非语言的 bug,但和语言的实现原理有关, js 所有数字统一为 Number, 包括整形实际上全都是双精度(double)类型。
而PHP会区分 int 还是 float。不管什么语言,只要涉及浮点运算,都是存在类似的问题,使用时一定要注意。
根据国际标准IEEE 754,任意一个二进制浮点数V可以表示成下面的形式:
class="java" name="code">V = (-1)s * M * E
1. (-1)s 表示符号位,当s=0,V为正数;当s=1,V为负数。
2. M表示有效数字,大于等于1,小于2。
3. 2E 表示指数位。
?举例来说:十进制的-5.0,写成二进制是-101.0,相当于-1.01×22 。那么,s=1,M=1.01,E=2。
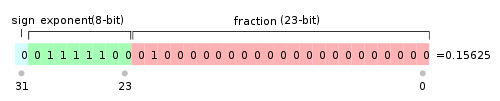
IEEE 754规定,对于32位的浮点数,最高的1位是符号位s,接着的8位是指数E,剩下的23位为有效数字M。
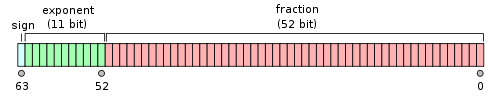
对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。
IEEE 754对有效数字M和指数E,还有一些特别规定。
前面说过,1≤M<2,也就是说,M可以写成1.xxxxxx的形式,其中xxxxxx表示小数部分。IEEE 754规定,在计算机 内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。比如保存1.01的时候,只 保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位浮点数为例,留给 M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字。
至于指数E,情况就比较复杂。
首先,E为一个无符号整数(unsigned int)。这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它 的取值范围为0~2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,E的真实值必须 由E再减去一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。
比如,210 的E是10,所以保存成32位浮点数时,必须保存成10(E的真实值)+127=137(E),即10001001。
然后,指数E还可以再分成三种情况:
(1)E不全为0或不全为1。这时,浮点数就采用上面的规则表示,即指数E的计算值减去127(或1023),得到真实 值,再将有效数字M前加上第一位的1。
(2)E全为0。这时,浮点数的指数E等于1-127(或者1-1023),有效数字M不再加上第一位的1,而是还原为 0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
(3)E全为1。这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);如果有效数字M不全为0,表示 这个数不是一个数(NaN)。>
http://www.laruence.com/2013/03/26/2884.html
http://www.cnblogs.com/qlwy/archive/2012/08/17/2644470.html
?
转自:http://www.yinqisen.cn/blog-782.html