算法（第四版）C#题解——1.5_.NET_编程开发_程序员俱乐部

写在前面

整个项目都托管在了 Github 上：https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp

这一节内容可能会用到的库文件有 Measurement 和 TestCase，同样在 Github 上可以找到。

善用 Ctrl + F 查找题目。

习题&题解

1.5.1

题目

使用 quick-find 算法处理序列 9-0 3-4 5-8 7-2 2-1 5-7 0-3 4-2 。
对于输入的每一对整数，给出 id[] 数组的内容和访问数组的次数。

解答

quick-find 的官方实现：QuickFindUF.java。

只要实现相应并查集，然后输入内容即可。

增加一个记录访问数组次数的类成员变量，在每次访问数组的语句执行后自增即可。

样例输出：

0 1 2 3 4 5 6 7 8 0 数组访问：13
0 1 2 4 4 5 6 7 8 0 数组访问：13
0 1 2 4 4 8 6 7 8 0 数组访问：13
0 1 2 4 4 8 6 2 8 0 数组访问：13
0 1 1 4 4 8 6 1 8 0 数组访问：14
0 1 1 4 4 1 6 1 1 0 数组访问：14
4 1 1 4 4 1 6 1 1 4 数组访问：14
1 1 1 1 1 1 6 1 1 1 数组访问：16

代码

QuickFindUF.cs，这个类继承了 UF.cs，重新实现了 Union() 和 Find() 等方法。

关于 UF.cs 可以参见原书中文版 P138 或英文版 P221 的算法 1.5。

namespace UnionFind
{
    /// <summary>
    /// 用 QuickFind 算法实现的并查集。
    /// </summary>
    public class QuickFindUF : UF
    {
        public int ArrayVisitCount { get; private set; } //记录数组访问的次数。

        /// <summary>
        /// 新建一个使用 quick-find 实现的并查集。
        /// </summary>
        /// <param name="n">并查集的大小。</param>
        public QuickFindUF(int n) : base(n) { }

        /// <summary>
        /// 重置数组访问计数。
        /// </summary>
        public void ResetArrayCount()
        {
            this.ArrayVisitCount = 0;
        }
        
        /// <summary>
        /// 寻找 p 所在的连通分量。
        /// </summary>
        /// <param name="p">需要寻找的结点。</param>
        /// <returns>返回 p 所在的连通分量。</returns>
        public override int Find(int p)
        {
            Validate(p);
            this.ArrayVisitCount++;
            return this.parent[p];
        }

        /// <summary>
        /// 判断两个结点是否属于同一个连通分量。
        /// </summary>
        /// <param name="p">需要判断的结点。</param>
        /// <param name="q">需要判断的另一个结点。</param>
        /// <returns>如果属于同一个连通分量则返回 true，否则返回 false。</returns>
        public override bool IsConnected(int p, int q)
        {
            Validate(p);
            Validate(q);
            this.ArrayVisitCount += 2;
            return this.parent[p] == this.parent[q];
        }

        /// <summary>
        /// 将两个结点所在的连通分量合并。
        /// </summary>
        /// <param name="p">需要合并的结点。</param>
        /// <param name="q">需要合并的另一个结点。</param>
        public override void Union(int p, int q)
        {
            Validate(p);
            Validate(q);
            int pID = this.parent[p];
            int qID = this.parent[q];
            this.ArrayVisitCount += 2;

            // 如果两个结点同属于一个连通分量，那么什么也不做。
            if (pID == qID)
            {
                return;
            }

            for (int i = 0; i < this.parent.Length; ++i)
            {
                if (this.parent[i] == pID)
                {
                    this.parent[i] = qID;
                    this.ArrayVisitCount++;
                }
            }

            this.ArrayVisitCount += this.parent.Length;
            this.count--;
            return;
        }

        /// <summary>
        /// 获得 parent 数组。
        /// </summary>
        /// <returns>id 数组。</returns>
        public int[] GetParent()
        {
            return this.parent;
        }
    }
}

Main 方法：

using System;
using UnionFind;

namespace _1._5._1
{
    /*
     * 1.5.1
     * 
     * 使用 quick-find 算法处理序列 9-0 3-4 5-8 7-2 2-1 5-7 0-3 4-2 。
     * 对于输入的每一对整数，给出 id[] 数组的内容和访问数组的次数。
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            string[] input = "9-0 3-4 5-8 7-2 2-1 5-7 0-3 4-2".Split(' ');
            var quickFind = new QuickFindUF(10);

            foreach (string s in input)
            {
                quickFind.ResetArrayCount();

                string[] numbers = s.Split('-');
                int p = int.Parse(numbers[0]);
                int q = int.Parse(numbers[1]);

                int[] id = quickFind.GetParent();
                quickFind.Union(p, q);
                foreach (int root in id)
                {
                    Console.Write(root + " ");
                }
                Console.WriteLine("数组访问：" + quickFind.ArrayVisitCount);
            }
        }
    }
}

 

1.5.2

题目

使用 quick-union 算法（请见 1.5.2.3 节代码框）完成练习 1.5.1。
另外，在处理完输入的每对整数之后画出 id[] 数组表示的森林。

解答

quick-union 的官方实现：QuickUnionUF.java。

和上题一样的方式，增加一个记录访问数组次数的类成员变量，在每次访问数组的语句执行后自增即可。

程序输出的森林，用缩进表示子树：

|---- 0
    |---- 9
|---- 1
|---- 2
|---- 3
|---- 4
|---- 5
|---- 6
|---- 7
|---- 8
数组访问：1
|---- 0
    |---- 9
|---- 1
|---- 2
|---- 4
    |---- 3
|---- 5
|---- 6
|---- 7
|---- 8
数组访问：1
|---- 0
    |---- 9
|---- 1
|---- 2
|---- 4
    |---- 3
|---- 6
|---- 7
|---- 8
    |---- 5
数组访问：1
|---- 0
    |---- 9
|---- 1
|---- 2
    |---- 7
|---- 4
    |---- 3
|---- 6
|---- 8
    |---- 5
数组访问：1
|---- 0
    |---- 9
|---- 1
    |---- 2
        |---- 7
|---- 4
    |---- 3
|---- 6
|---- 8
    |---- 5
数组访问：1
|---- 0
    |---- 9
|---- 1
    |---- 2
        |---- 7
    |---- 8
        |---- 5
|---- 4
    |---- 3
|---- 6
数组访问：7
|---- 1
    |---- 2
        |---- 7
    |---- 8
        |---- 5
|---- 4
    |---- 0
        |---- 9
    |---- 3
|---- 6
数组访问：3
|---- 1
    |---- 2
        |---- 7
    |---- 4
        |---- 0
            |---- 9
        |---- 3
    |---- 8
        |---- 5
|---- 6
数组访问：3

代码

QuickUnionUF.cs，这个类继承了 UF.cs，重新实现了 Union() 和 Find() 等方法。

关于 UF.cs 可以参见原书中文版 P138 或英文版 P221 的算法 1.5。

namespace UnionFind
{
    /// <summary>
    /// 用 QuickUnion 算法实现的并查集。
    /// </summary>
    public class QuickUnionUF : UF
    {
        public int ArrayVisitCount { get; private set; } //记录数组访问的次数。

        /// <summary>
        /// 建立使用 QuickUnion 的并查集。
        /// </summary>
        /// <param name="n">并查集的大小。</param>
        public QuickUnionUF(int n) : base(n) { }

        /// <summary>
        /// 重置数组访问计数。
        /// </summary>
        public virtual void ResetArrayCount()
        {
            this.ArrayVisitCount = 0;
        }

        /// <summary>
        /// 获得 parent 数组。
        /// </summary>
        /// <returns>返回 parent 数组。</returns>
        public int[] GetParent()
        {
            return this.parent;
        }

        /// <summary>
        /// 寻找一个结点所在的连通分量。
        /// </summary>
        /// <param name="p">需要寻找的结点。</param>
        /// <returns>该结点所属的连通分量。</returns>
        public override int Find(int p)
        {
            Validate(p);
            while (p != this.parent[p])
            {
                p = this.parent[p];
                this.ArrayVisitCount += 2;
            }
            return p;
        }

        /// <summary>
        /// 将两个结点所属的连通分量合并。
        /// </summary>
        /// <param name="p">需要合并的结点。</param>
        /// <param name="q">需要合并的另一个结点。</param>
        public override void Union(int p, int q)
        {
            int rootP = Find(p);
            int rootQ = Find(q);
            if (rootP == rootQ)
            {
                return;
            }

            this.parent[rootP] = rootQ;
            this.ArrayVisitCount++;
            this.count--;
        }
    }

}

Main 方法

using System;
using UnionFind;

namespace _1._5._2
{
    /*
     * 1.5.2
     * 
     * 使用 quick-union 算法（请见 1.5.2.3 节代码框）完成练习 1.5.1。
     * 另外，在处理完输入的每对整数之后画出 id[] 数组表示的森林。
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            string[] input = "9-0 3-4 5-8 7-2 2-1 5-7 0-3 4-2".Split(' ');
            var quickUnion = new QuickUnionUF(10);

            foreach (string s in input)
            {
                quickUnion.ResetArrayCount();
                string[] numbers = s.Split('-');
                int p = int.Parse(numbers[0]);
                int q = int.Parse(numbers[1]);

                quickUnion.Union(p, q);
                int[] parent = quickUnion.GetParent();
                for (int i = 0; i < parent.Length; ++i)
                {
                    if (parent[i] == i)
                    {
                        Console.WriteLine("|---- " + i);
                        DFS(parent, i, 1);
                    }
                }
                Console.WriteLine("数组访问：" + quickUnion.ArrayVisitCount);
            }
        }

        static void DFS(int[] parent, int root, int level)
        {
            for (int i = 0; i < parent.Length; ++i)
            {
                if (parent[i] == root && i != root)
                {
                    for (int j = 0; j < level; ++j)
                    {
                        Console.Write("    ");
                    }
                    Console.WriteLine("|---- " + i);
                    DFS(parent, i, level + 1);
                }
            }
        }
    }
}

1.5.3

题目

使用加权 quick-union 算法（请见算法 1.5）完成练习 1.5.1 。

解答

加权 quick-union 的官方实现：WeightedQuickUnionUF.java。

样例输出：

9 1 2 3 4 5 6 7 8 9 数组访问：3
9 1 2 3 3 5 6 7 8 9 数组访问：3
9 1 2 3 3 5 6 7 5 9 数组访问：3
9 1 7 3 3 5 6 7 5 9 数组访问：3
9 7 7 3 3 5 6 7 5 9 数组访问：5
9 7 7 3 3 7 6 7 5 9 数组访问：3
9 7 7 9 3 7 6 7 5 9 数组访问：5
9 7 7 9 3 7 6 7 5 7 数组访问：9

代码

WeightedQuickUnionUF.cs，这个类继承了 QuickUnion.cs，重新实现了 Union() 和 Find() 等方法。

关于 QuickUnion.cs 可以参见 1.5.2 的代码部分。

namespace UnionFind
{
    /// <summary>
    /// 使用加权 quick-union 算法的并查集。
    /// </summary>
    public class WeightedQuickUnionUF : QuickUnionUF
    {
        protected int[] size; // 记录各个树的大小。

        public int ArrayParentVisitCount { get; private set; } // 记录 parent 数组的访问次数。
        public int ArraySizeVisitCount { get; private set; } //记录 size 数组的访问次数。

        /// <summary>
        /// 建立使用加权 quick-union 的并查集。
        /// </summary>
        /// <param name="n">并查集的大小。</param>
        public WeightedQuickUnionUF(int n) : base(n)
        {
            this.size = new int[n];
            for (int i = 0; i < n; ++i)
            {
                this.size[i] = 1;
            }
            this.ArrayParentVisitCount = 0;
            this.ArraySizeVisitCount = 0;
        }

        /// <summary>
        /// 清零数组访问计数。
        /// </summary>
        public override void ResetArrayCount()
        {
            this.ArrayParentVisitCount = 0;
            this.ArraySizeVisitCount = 0;
        }

        /// <summary>
        /// 获取 size 数组。
        /// </summary>
        /// <returns>返回 size 数组。</returns>
        public int[] GetSize()
        {
            return this.size;
        }

        /// <summary>
        /// 寻找一个结点所在的连通分量。
        /// </summary>
        /// <param name="p">需要寻找的结点。</param>
        /// <returns>该结点所属的连通分量。</returns>
        public override int Find(int p)
        {
            Validate(p);
            while (p != this.parent[p])
            {
                p = this.parent[p];
                this.ArrayParentVisitCount += 2;
            }
            this.ArrayParentVisitCount++;
            return p;
        }

        /// <summary>
        /// 将两个结点所属的连通分量合并。
        /// </summary>
        /// <param name="p">需要合并的结点。</param>
        /// <param name="q">需要合并的另一个结点。</param>
        public override void Union(int p, int q)
        {
            int rootP = Find(p);
            int rootQ = Find(q);
            if (rootP == rootQ)
            {
                return;
            }

            if (this.size[rootP] < this.size[rootQ])
            {
                this.parent[rootP] = rootQ;
                this.size[rootQ] += this.size[rootP];
            }
            else
            {
                this.parent[rootQ] = rootP;
                this.size[rootP] += this.size[rootQ];
            }
            this.ArrayParentVisitCount++;
            this.ArraySizeVisitCount += 4;
            this.count--;
        }
    }
}

Main 方法

using System;
using UnionFind;

namespace _1._5._3
{
    /*
     * 1.5.3
     * 
     * 使用加权 quick-union 算法（请见算法 1.5）完成练习 1.5.1 。
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            string[] input = "9-0 3-4 5-8 7-2 2-1 5-7 0-3 4-2".Split(' ');
            var weightedQuickUnion = new WeightedQuickUnionUF(10);

            foreach (string s in input)
            {
                weightedQuickUnion.ResetArrayCount();
                string[] numbers = s.Split('-');
                int p = int.Parse(numbers[0]);
                int q = int.Parse(numbers[1]);

                weightedQuickUnion.Union(p, q);
                int[] parent = weightedQuickUnion.GetParent();
                for (int i = 0; i < parent.Length; ++i)
                {
                    Console.Write(parent[i] + " ");
                }
                Console.WriteLine("数组访问：" + weightedQuickUnion.ArrayParentVisitCount);
            }
        }
    }
}

1.5.4

题目

在正文的加权 quick-union 算法示例中，对于输入的每一对整数（包括对照输入和最坏情况下的输入），给出 id[] 和 sz[] 数组的内容以及访问数组的次数。

解答

对照输入和最坏输入均在书中出现，中文版见：P146，英文版见：P229。

样例输出：

4 3
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 1 2 4 4 5 6 7 8 9
size:   1 1 1 1 2 1 1 1 1 1
parent visit count:3
size visit count:4

3 8
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 1 2 4 4 5 6 7 4 9
size:   1 1 1 1 3 1 1 1 1 1
parent visit count:5
size visit count:4

6 5
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 1 2 4 4 6 6 7 4 9
size:   1 1 1 1 3 1 2 1 1 1
parent visit count:3
size visit count:4

9 4
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 1 2 4 4 6 6 7 4 4
size:   1 1 1 1 4 1 2 1 1 1
parent visit count:3
size visit count:4

2 1
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 2 2 4 4 6 6 7 4 4
size:   1 1 2 1 4 1 2 1 1 1
parent visit count:3
size visit count:4

8 9
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 2 2 4 4 6 6 7 4 4
size:   1 1 2 1 4 1 2 1 1 1
parent visit count:6
size visit count:0

5 0
index:  0 1 2 3 4 5 6 7 8 9
parent: 6 2 2 4 4 6 6 7 4 4
size:   1 1 2 1 4 1 3 1 1 1
parent visit count:5
size visit count:4

7 2
index:  0 1 2 3 4 5 6 7 8 9
parent: 6 2 2 4 4 6 6 2 4 4
size:   1 1 3 1 4 1 3 1 1 1
parent visit count:3
size visit count:4

6 1
index:  0 1 2 3 4 5 6 7 8 9
parent: 6 2 6 4 4 6 6 2 4 4
size:   1 1 3 1 4 1 6 1 1 1
parent visit count:5
size visit count:4

1 0
index:  0 1 2 3 4 5 6 7 8 9
parent: 6 2 6 4 4 6 6 2 4 4
size:   1 1 3 1 4 1 6 1 1 1
parent visit count:8
size visit count:0

6 7
index:  0 1 2 3 4 5 6 7 8 9
parent: 6 2 6 4 4 6 6 2 4 4
size:   1 1 3 1 4 1 6 1 1 1
parent visit count:6
size visit count:0

-------------------------------------
0 1
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 0 2 3 4 5 6 7 8 9
size:   2 1 1 1 1 1 1 1 1 1
parent visit count:3
size visit count:4

0 2
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 0 0 3 4 5 6 7 8 9
size:   3 1 1 1 1 1 1 1 1 1
parent visit count:3
size visit count:4

0 3
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 0 0 0 4 5 6 7 8 9
size:   4 1 1 1 1 1 1 1 1 1
parent visit count:3
size visit count:4

0 4
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 0 0 0 0 5 6 7 8 9
size:   5 1 1 1 1 1 1 1 1 1
parent visit count:3
size visit count:4

0 5
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 0 0 0 0 0 6 7 8 9
size:   6 1 1 1 1 1 1 1 1 1
parent visit count:3
size visit count:4

0 6
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 0 0 0 0 0 0 7 8 9
size:   7 1 1 1 1 1 1 1 1 1
parent visit count:3
size visit count:4

0 7
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 0 0 0 0 0 0 0 8 9
size:   8 1 1 1 1 1 1 1 1 1
parent visit count:3
size visit count:4

0 8
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 0 0 0 0 0 0 0 0 9
size:   9 1 1 1 1 1 1 1 1 1
parent visit count:3
size visit count:4

0 9
index:  0 1 2 3 4 5 6 7 8 9
parent: 0 0 0 0 0 0 0 0 0 0
size:   10 1 1 1 1 1 1 1 1 1
parent visit count:3
size visit count:4

代码

Main 方法：

using System;
using UnionFind;

namespace _1._5._4
{
    /*
     * 1.5.4
     * 
     * 在正文的加权 quick-union 算法示例中，
     * 对于输入的每一对整数（包括对照输入和最坏情况下的输入），
     * 给出 id[] 和 sz[] 数组的内容以及访问数组的次数。
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            char[] split = { '\n', '\r' };
            string[] inputReference = TestCase.Properties.Resources.tinyUF.Split(split, StringSplitOptions.RemoveEmptyEntries);
            string[] inputWorst = TestCase.Properties.Resources.worstUF.Split(split, StringSplitOptions.RemoveEmptyEntries);
            
            RunTest(inputReference);
            Console.WriteLine("-------------------------------------");
            RunTest(inputWorst);
        }

        static void RunTest(string[] input)
        {
            var weightedQuickUnion = new WeightedQuickUnionUF(10);
            int n = int.Parse(input[0]);
            int[] parent = weightedQuickUnion.GetParent();
            int[] size = weightedQuickUnion.GetSize();

            for (int i = 1; i < input.Length; ++i)
            {
                string[] unit = input[i].Split(' ');
                int p = int.Parse(unit[0]);
                int q = int.Parse(unit[1]);

                Console.WriteLine($"{p} {q}");
                weightedQuickUnion.Union(p, q);

                Console.Write("index:\t");
                for (int j = 0; j < 10; ++j)
                {
                    Console.Write(j + " ");
                }
                Console.WriteLine();

                Console.Write("parent:\t");
                foreach (int m in parent)
                {
                    Console.Write(m + " ");
                }
                Console.WriteLine();
                Console.Write("size:\t");
                foreach (int m in size)
                {
                    Console.Write(m + " ");
                }
                Console.WriteLine();
                Console.WriteLine("parent visit count:" + weightedQuickUnion.ArrayParentVisitCount);
                Console.WriteLine("size visit count:" + weightedQuickUnion.ArraySizeVisitCount);
                Console.WriteLine();
                weightedQuickUnion.ResetArrayCount();
            }
        }
    }
}

1.5.5

题目

在一台每秒能够处理 10^9 条指令的计算机上，估计 quick-find 算法解决含有 10^9 个触点和 10^6 条连接的动态连通性问题所需的最短时间（以天记）。
假设内循环 for 的每一次迭代需要执行 10 条机器指令。

解答

10⁶ 条连接 = 10⁶ 组输入。
对于 quick-find 算法，每次 union() 都要遍历整个数组。
因此总共进行了 10⁹ * 10⁶ = 10¹⁵ 次 for 循环迭代。
每次 for 循环迭代都需要 10 条机器指令，
因此总共执行了 10 * 10¹⁵ = 10¹⁶ 条机器指令。
已知计算机每秒能够执行 10⁹ 条机器指令，
因此执行完所有指令需要 10¹⁶ / 10⁹ = 10⁷ 秒 = 115.74 天

1.5.6

题目

使用加权 quick-union 算法完成练习 1.5.5 。

解答

加权 quick-union 算法最多只需要 lgN 次迭代就可以完成一次 union()。
因此按照上题思路，总共需要 (lg(10⁹) * 10⁶ * 10) / 10⁹ = 0.299 秒。

1.5.7

题目

分别为 quick-find 算法和 quick-union 算法实现 QuickFindUF 类和  QuickUnionUF 类。

解答

见 1.5.1 和 1.5.2 的解答。

1.5.8

题目

用一个反例证明 quick-find 算法中的 union() 方法的以下直观实现是错误的：

public void union(int p, int q)
{
    if (connected(p, q)) return;
    for (int I = 0; I < id.length; I++)
    {
        if (id[i] == id[p]) id[i] = id[q];
    }
    count--;
}

解答

当有多个元素需要修改的时候，这个直观算法可能会出现错误。
例如如下情况：
index 0 1 2 3 4 5 6 7 8 9
id    0 0 0 0 0 5 5 5 5 5
输入 0, 5
i = 0 时，id[i] == id[p]，此时 id[i] = id[q]。
数组变为 5 0 0 0 0 5 5 5 5 5
i = 1 时，id[i] != id[p]，算法出现错误。

如果在 id[p] 之后还有需要修改的元素，那么这个算法就会出现错误。

1.5.9

题目

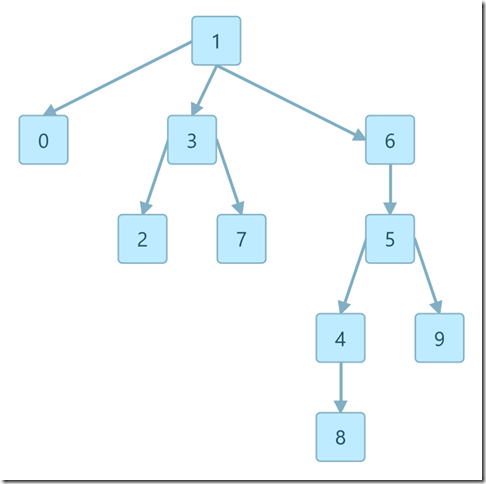
画出下面的 id[] 数组所对应的树。这可能是加权 quick-union 算法得到的结果吗？
解释为什么不可能，或者给出能够得到该数组的一系列操作。

                 i                             0 1 2 3 4 5 6 7 8 9
------------------------------------------------------------------------------------------------
                id[i]                          1 1 3 1 5 6 1 3 4 5

解答

不可能。
树如下所示。

由于加权 quick-union 算法任意节点的最大深度为 lgN （节点总数为 N）。
（这个结论可以在中文版 P146，或者英文版 P228 找到）
上面这个树的最大深度为 4 > lg10
因此这棵树不可能是通过加权 quick-union 算法得到的。

1.5.10

题目

在加权 quick-union 算法中，假设我们将 id[find(p)] 的值设为 q 而非 id[find[q]]，所得的算法是正确的吗？
答：是，但这会增加树的高度，因此无法保证同样的性能。

解答

本题答案已经给出，也很好理解。

如果合并时只是把子树挂到结点 q 上而非其根节点，树的高度会明显增加，进而增加每次 Find() 操作的开销。

1.5.11

题目

实现加权 quick-find 算法，其中我们总是将较小的分量重命名为较大分量的标识符。
这种改变会对性能产生怎样的影响？

解答

类似于加权 quick-union 的做法，新增一个 size[] 数组以记录各个根节点的大小。

每次合并时先比较一下两棵树的大小，再进行合并。

这样会略微减少赋值语句的执行次数，提升性能。

代码

WeightedQuickFindUF.cs

using System;

namespace _1._5._11
{
    /// <summary>
    /// 用加权 QuickFind 算法实现的并查集。
    /// </summary>
    public class WeightedQuickFindUF
    {
        private int[] size; // 记录每个连通分量的大小。
        private int[] id; // 记录每个结点的连通分量。
        private int count;// 连通分量总数。

        public int ArrayVisitCount { get; private set; } //记录数组访问的次数。

        /// <summary>
        /// 新建一个使用加权 quick-find 实现的并查集。
        /// </summary>
        /// <param name="n">并查集的大小。</param>
        public WeightedQuickFindUF(int n)
        {
            this.count = n;
            this.id = new int[n];
            this.size = new int[n];
            for (int i = 0; i < n; ++i)
            {
                this.id[i] = i;
                this.size[i] = 1;
            }
        }

        /// <summary>
        /// 重置数组访问计数。
        /// </summary>
        public void ResetArrayCount()
        {
            this.ArrayVisitCount = 0;
        }

        /// <summary>
        /// 表示并查集中连通分量的数量。
        /// </summary>
        /// <returns>返回并查集中连通分量的数量。</returns>
        public int Count()
        {
            return this.count;
        }
        
        /// <summary>
        /// 寻找 p 所在的连通分量。
        /// </summary>
        /// <param name="p">需要寻找的结点。</param>
        /// <returns>返回 p 所在的连通分量。</returns>
        public int Find(int p)
        {
            Validate(p);
            this.ArrayVisitCount++;
            return this.id[p];
        }

        /// <summary>
        /// 判断两个结点是否属于同一个连通分量。
        /// </summary>
        /// <param name="p">需要判断的结点。</param>
        /// <param name="q">需要判断的另一个结点。</param>
        /// <returns>如果属于同一个连通分量则返回 true，否则返回 false。</returns>
        public bool IsConnected(int p, int q)
        {
            Validate(p);
            Validate(q);
            this.ArrayVisitCount += 2;
            return this.id[p] == this.id[q];
        }

        /// <summary>
        /// 将两个结点所在的连通分量合并。
        /// </summary>
        /// <param name="p">需要合并的结点。</param>
        /// <param name="q">需要合并的另一个结点。</param>
        public void Union(int p, int q)
        {
            Validate(p);
            Validate(q);
            int pID = this.id[p];
            int qID = this.id[q];
            this.ArrayVisitCount += 2;

            // 如果两个结点同属于一个连通分量，那么什么也不做。
            if (pID == qID)
            {
                return;
            }

            // 判断较大的连通分量和较小的连通分量。
            int larger = 0;
            int smaller = 0;
            if (this.size[pID] > this.size[qID])
            {
                larger = pID;
                smaller = qID;
                this.size[pID] += this.size[qID];
            }
            else
            {
                larger = qID;
                smaller = pID;
                this.size[qID] += this.size[pID];
            }

            // 将较小的连通分量连接到较大的连通分量上，
            // 这会减少赋值语句的执行次数，略微减少数组访问。
            for (int i = 0; i < this.id.Length; ++i)
            {
                if (this.id[i] == smaller)
                {
                    this.id[i] = larger;
                    this.ArrayVisitCount++;
                }
            }

            this.ArrayVisitCount += this.id.Length;
            this.count--;
            return;
        }

        /// <summary>
        /// 获得 id 数组。
        /// </summary>
        /// <returns>id 数组。</returns>
        public int[] GetID()
        {
            return this.id;
        }

        /// <summary>
        /// 验证输入的结点是否有效。
        /// </summary>
        /// <param name="p">需要验证的结点。</param>
        /// <exception cref="ArgumentException">输入的 p 值无效。</exception>
        private void Validate(int p)
        {
            int n = this.id.Length;
            if (p < 0 || p > n)
            {
                throw new ArgumentException("index " + p + " is not between 0 and " + (n - 1));
            }
        }
    }
}

Main 方法

using System;
using UnionFind;

namespace _1._5._11
{
    /*
     * 1.5.11
     * 
     * 实现加权 quick-find 算法，其中我们总是将较小的分量重命名为较大分量的标识符。
     * 这种改变会对性能产生怎样的影响？
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            char[] split = { '\n', '\r' };
            string[] input = TestCase.Properties.Resources.mediumUF.Split(split, StringSplitOptions.RemoveEmptyEntries);
            int size = int.Parse(input[0]);

            QuickFindUF quickFind = new QuickFindUF(size);
            WeightedQuickFindUF weightedQuickFind = new WeightedQuickFindUF(size);

            int p, q;
            string[] pair;
            for (int i = 1; i < size; ++i)
            {
                pair = input[i].Split(' ');
                p = int.Parse(pair[0]);
                q = int.Parse(pair[1]);
                quickFind.Union(p, q);
                weightedQuickFind.Union(p, q);
            }

            Console.WriteLine("quick-find: " + quickFind.ArrayVisitCount);
            Console.WriteLine("weighted quick-find: " + weightedQuickFind.ArrayVisitCount);
        }
    }
}

1.5.12

题目

使用路径压缩的 quick-union 算法。
根据路径压缩修改 quick-union 算法（请见 1.5.2.3 节），在 find() 方法中添加一个循环来将从 p 到根节点的路径上的每个触点都连接到根节点。
给出一列输入，使该方法能够产生一条长度为 4 的路径。
注意：该算法的所有操作的均摊成本已知为对数级别。

解答

QuickUnionPathCompression 的官方实现：QuickUnionPathCompressionUF.java

在找到根节点之后，再访问一遍 p 到根节点这条路径上的所有结点，将它们直接和根节点相连。

重写过后的 Find() 方法：

/// <summary>
/// 寻找结点所属的连通分量。
/// </summary>
/// <param name="p">需要寻找的结点。</param>
/// <returns>结点所属的连通分量。</returns>
public override int Find(int p)
{
    int root = p;
    while (root != this.parent[root])
    {
        root = this.parent[root];
    }
    while (p != root)
    {
        int newp = this.parent[p];
        this.parent[p] = root;
        p = newp;
    }
    return p;
}

由于路径压缩是在 Find() 方法中实现的，只要输入保证是根节点两两相连即可构造较长的路径。

代码

QuickUnionPathCompressionUF.cs 直接从 QuickUnionUF.cs 继承而来。
关于 QuickUnionUF.cs，参见 1.5.2 的解答。

namespace UnionFind
{
    /// <summary>
    /// 使用路径压缩的 quick-union 并查集。
    /// </summary>
    public class QuickUnionPathCompressionUF : QuickFindUF
    {
        /// <summary>
        /// 新建一个大小为 n 的并查集。
        /// </summary>
        /// <param name="n">新建并查集的大小。</param>
        public QuickUnionPathCompressionUF(int n) : base(n) { }

        /// <summary>
        /// 寻找结点所属的连通分量。
        /// </summary>
        /// <param name="p">需要寻找的结点。</param>
        /// <returns>结点所属的连通分量。</returns>
        public override int Find(int p)
        {
            int root = p;
            while (root != this.parent[root])
            {
                root = this.parent[root];
            }
            while (p != root)
            {
                int newp = this.parent[p];
                this.parent[p] = root;
                p = newp;
            }
            return p;
        }
    }
}

Main 方法

using System;
using UnionFind;

namespace _1._5._12
{
    /*
     * 1.5.12
     * 
     * 使用路径压缩的 quick-union 算法。
     * 根据路径压缩修改 quick-union 算法（请见 1.5.2.3 节），
     * 在 find() 方法中添加一个循环来将从 p 到根节点的路径上的每个触点都连接到根节点。
     * 给出一列输入，使该方法能够产生一条长度为 4 的路径。
     * 注意：该算法的所有操作的均摊成本已知为对数级别。
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            var UF = new QuickUnionPathCompressionUF(10);

            // 使用书中提到的最坏情况，0 连 1，1 连 2，2 连 3……
            for (int i = 0; i < 4; ++i)
            {
                UF.Union(i, i + 1);
            }

            int[] id = UF.GetParent();
            for (int i = 0; i < id.Length; ++i)
            {
                Console.Write(id[i]);
            }
            Console.WriteLine();
        }
    }
}

1.5.13

题目

使用路径压缩的加权 quick-union 算法。
修改加权 quick-union 算法（算法 1.5），实现如练习 1.5.12 所述的路径压缩。
给出一列输入，使该方法能产生一棵高度为 4 的树。
注意：该算法的所有操作的均摊成本已知被限制在反 Ackermann 函数的范围之内，且对于实际应用中可能出现的所有 N 值均小于 5。

解答

官方实现：WeightedQuickUnionPathCompressionUF。

加权 quick-union 中，两个大小相等的树合并可以有效增加高度，同时输入必须保证是根节点以规避路径压缩。

代码

WeightedQuickUnionPathCompressionUF.cs 从 WeightedQuickUnionUF.cs 继承，详情参见 1.5.3 的解答。

namespace UnionFind
{
    /// <summary>
    /// 使用路径压缩的加权 quick-union 并查集。
    /// </summary>
    public class WeightedQuickUnionPathCompressionUF : WeightedQuickUnionUF
    {
        /// <summary>
        /// 新建一个大小为 n 的并查集。
        /// </summary>
        /// <param name="n">新建并查集的大小。</param>
        public WeightedQuickUnionPathCompressionUF(int n) : base(n)
        {
            this.size = new int[n];

            for (int i = 0; i < n; ++i)
            {
                this.size[i] = 1;
            }
        }

        /// <summary>
        /// 寻找一个结点所在的连通分量。
        /// </summary>
        /// <param name="p">需要寻找的结点。</param>
        /// <returns>该结点所属的连通分量。</returns>
        public override int Find(int p)
        {
            Validate(p);
            int root = p;
            while (root != this.parent[p])
            {
                root = this.parent[p];
            }
            while (p != root)
            {
                int newP = this.parent[p];
                this.parent[p] = root;
                p = newP;
            }
            return root;
        }
    }
}

Main 方法

using System;
using UnionFind;

namespace _1._5._13
{
    /*
     * 1.5.13
     * 
     * 使用路径压缩的加权 quick-union 算法。
     * 修改加权 quick-union 算法（算法 1.5），
     * 实现如练习 1.5.12 所述的路径压缩。给出一列输入，
     * 使该方法能产生一棵高度为 4 的树。
     * 注意：该算法的所有操作的均摊成本已知被限制在反 Ackermann 函数的范围之内，
     * 且对于实际应用中可能出现的所有 N 值均小于 5。
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            var UF = new WeightedQuickUnionPathCompressionUF(10);

            // 见中文版 P146 或英文版 P229 中加权 quick-union 的最坏输入。
            UF.Union(0, 1);
            UF.Union(2, 3);
            UF.Union(4, 5);
            UF.Union(6, 7);
            UF.Union(0, 2);
            UF.Union(4, 6);
            UF.Union(0, 4);

            int[] id = UF.GetParent();
            for (int i = 0; i < id.Length; ++i)
            {
                Console.Write(id[i]);
            }
            Console.WriteLine();
        }
    }
}

1.5.14

题目

根据高度加权的 quick-union 算法。
给出 UF 的一个实现，使用和加权 quick-union 算法相同的策略，但记录的是树的高度并总是将较矮的树连接到较高的树上。
用算法证明 N 个触点的树的高度不会超过其大小的对数级别。

解答

WeightedQuickUnionByHeight 的官方实现：WeightedQuickUnionByHeightUF.java。

证明：
一次 Union 操作只可能发生如下两种情况。
1.两棵树的高度相同，这样合并后的新树的高度等于较大那棵树的高度 + 1。
2.两棵树的高度不同，这样合并后的新树高度等于较大那棵树的高度。

现在证明通过加权 quick-union 算法构造的高度为 h 的树至少包含 2^h 个结点。
基础情况，高度 h = 0, 结点数 k = 1。
为了使高度增加，必须用一棵高度相同的树合并，而 h = 0 时结点数一定是 1，则：
h = 1, k = 2
由于两棵大小不同的树合并，最大高度不会增加，只会增加结点数。
因此，每次都使用相同高度的最小树进行合并，有：
h = 2, k = 4
h = 3, k = 8
h = 4, k = 16
......
递推即可得到结论，k ≥ 2^h
因此 h <= lgk

代码

namespace UnionFind
{
    public class WeightedQuickUnionByHeightUF : QuickUnionUF
    {
        private int[] height;

        /// <summary>
        /// 新建一个以高度作为判断依据的加权 quick-union 并查集。
        /// </summary>
        /// <param name="n">新建并查集的大小。</param>
        public WeightedQuickUnionByHeightUF(int n) : base(n)
        {
            this.height = new int[n];
            for (int i = 0; i < n; ++i)
            {
                this.height[i] = 0;
            }
        }

        /// <summary>
        /// 将两个结点所属的连通分量合并。
        /// </summary>
        /// <param name="p">需要合并的结点。</param>
        /// <param name="q">需要合并的另一个结点。</param>
        public override void Union(int p, int q)
        {
            int rootP = Find(p);
            int rootQ = Find(q);

            if (rootP == rootQ)
            {
                return;
            }

            if (this.height[rootP] < this.height[rootQ])
            {
                this.parent[rootP] = rootQ;
            }
            else if (this.height[rootP] > this.height[rootQ])
            {
                this.parent[rootQ] = rootP;
            }
            else
            {
                this.parent[rootQ] = rootP;
                this.height[rootP]++;
            }
            this.count--;
        }
    }
}

1.5.15

题目

二项树。
请证明，对于加权 quick-union 算法，在最坏情况下树中的每一层的结点数均为二项式系数。
在这种情况下，计算含有 N=2^n 个节点的树中节点的平均深度。

解答

首先证明在最坏情况下加权 quick-union 算法生成的树中的每一层结点数均为二项式系数。

最坏情况下，每次 union 操作都是合并相同大小的树，如下图所示：

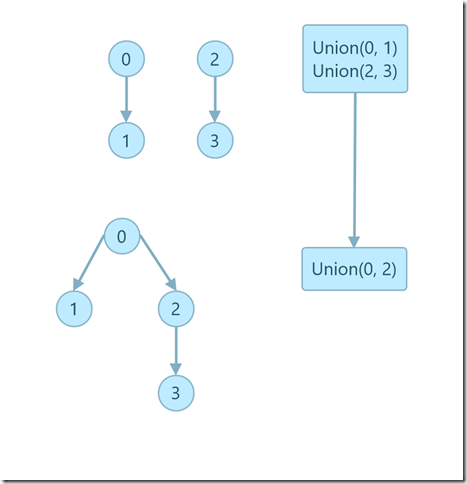
设第 i 层的结点数为 k_i，那么最坏情况下每次合并后的 k_i’ = k_i + k_{i-1 。}
这符合二项式系数的构造特点（详情可以搜索杨辉三角），第一个结论证明完毕。

接下来求平均深度，首先根据二项式的求和公式，一棵深度为 n 的树（根结点的深度为零）结点总数为：

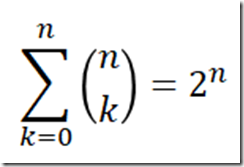
每层结点数 × 该层深度后的和为：

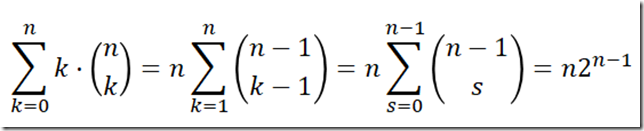
这里用到了这个公式化简：

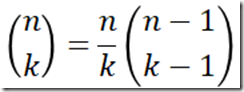
相除可以求得平均深度：

1.5.16

题目

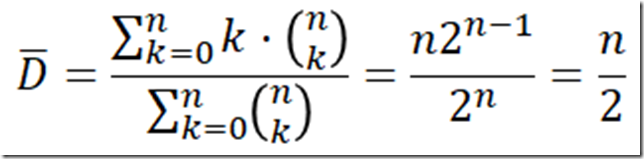
均摊成本的图像。修改你为练习 1.5.7 给出的实现，绘出如正文所示的均摊成本的图像。

解答

给出绘图结果样例：

代码

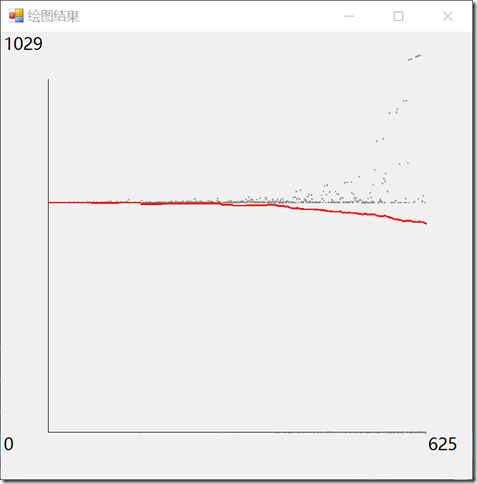
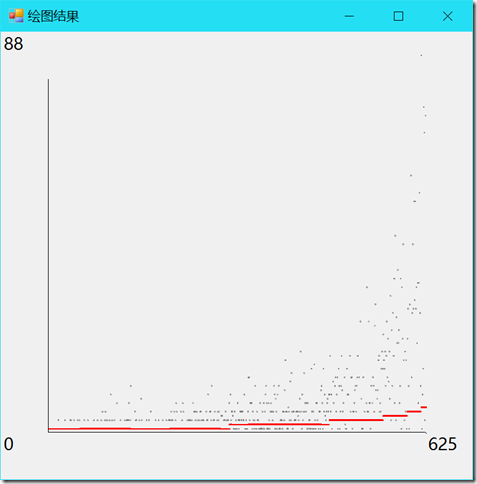
仅给出绘图相关的代码，窗体部分见 github 上的代码：

using System;
using System.Linq;
using System.Windows.Forms;
using System.Drawing;
using UnionFind;

namespace _1._5._16
{
    /*
    * 1.5.16
    * 
    * 均摊成本的图像。
    * 修改你为练习 1.5.7 给出的实现，
    * 绘出如正文所示的均摊成本的图像。
    * 
    */
    static class Program
    {
        [STAThread]
        static void Main()
        {
            Application.EnableVisualStyles();
            Application.SetCompatibleTextRenderingDefault(false);
            Compute();
            Application.Run(new Form1());
        }

        static void Compute()
        {
            char[] split = { '\n', '\r' };
            string[] input = TestCase.Properties.Resources.mediumUF.Split(split, StringSplitOptions.RemoveEmptyEntries);
            int size = int.Parse(input[0]);
            QuickFindUF quickFind = new QuickFindUF(size);
            QuickUnionUF quickUnion = new QuickUnionUF(size);

            string[] pair;
            int p, q;
            int[] quickFindResult = new int[size];
            int[] quickUnionResult = new int[size];
            for (int i = 1; i < size; ++i)
            {
                pair = input[i].Split(' ');
                p = int.Parse(pair[0]);
                q = int.Parse(pair[1]);

                quickFind.Union(p, q);
                quickUnion.Union(p, q);
                quickFindResult[i - 1] = quickFind.ArrayVisitCount;
                quickUnionResult[i - 1] = quickUnion.ArrayVisitCount;

                quickFind.ResetArrayCount();
                quickUnion.ResetArrayCount();
            }

            Draw(quickFindResult);
            Draw(quickUnionResult);
        }

        static void Draw(int[] cost)
        {
            // 构建 total 数组。
            int[] total = new int[cost.Length];
            total[0] = cost[0];
            for (int i = 1; i < cost.Length; ++i)
            {
                total[i] = total[i - 1] + cost[i];
            }

            // 获得最大值。
            int costMax = cost.Max();

            // 新建绘图窗口。
            Form2 plot = new Form2();
            plot.Show();
            Graphics graphics = plot.CreateGraphics();

            // 获得绘图区矩形。
            RectangleF rect = plot.ClientRectangle;
            float unitX = rect.Width / 10;
            float unitY = rect.Width / 10;

            // 添加 10% 边距作为文字区域。
            RectangleF center = new RectangleF
                (rect.X + unitX, rect.Y + unitY, 
                rect.Width - 2 * unitX, rect.Height - 2 * unitY);

            // 绘制坐标系。
            graphics.DrawLine(Pens.Black, center.Left, center.Top, center.Left, center.Bottom);
            graphics.DrawLine(Pens.Black, center.Left, center.Bottom, center.Right, center.Bottom);
            graphics.DrawString(costMax.ToString(), plot.Font, Brushes.Black, rect.Location);
            graphics.DrawString(cost.Length.ToString(), plot.Font, Brushes.Black, center.Right, center.Bottom);
            graphics.DrawString("0", plot.Font, Brushes.Black, rect.Left, center.Bottom);

            // 初始化点。
            PointF[] grayPoints = new PointF[cost.Length];
            PointF[] redPoints = new PointF[cost.Length];
            unitX = center.Width / cost.Length;
            unitY = center.Width / costMax;

            for (int i = 0; i < cost.Length; ++i)
            {
                grayPoints[i] = new PointF(center.Left + unitX * (i + 1), center.Bottom - (cost[i] * unitY));
                redPoints[i] = new PointF(center.Left + unitX * (i + 1), center.Bottom - ((total[i] / (i + 1)) * unitY));
            }

            // 绘制点。
            for (int i = 0; i < cost.Length; ++i)
            {
                graphics.DrawEllipse(Pens.Gray, new RectangleF(grayPoints[i], new SizeF(2, 2)));
                graphics.DrawEllipse(Pens.Red, new RectangleF(redPoints[i], new SizeF(2, 2)));
            }

            graphics.Dispose();
        }
    }
}

1.5.17

题目

随机链接。
设计 UF 的一个用例 ErdosRenyi，
从命令行接受一个整数 N，在 0 到 N-1 之间产生随机整数对，调用 connected() 判断它们是否相连，如果不是则调用 union() 方法（和我们的开发用例一样）。
不断循环直到所有触点均相互连通并打印出生成的连接总数。
将你的程序打包成一个接受参数 N 并返回连接总数的静态方法 count()，添加一个 main() 方法从命令行接受 N，调用 count() 并打印它的返回值。

解答

官方给出的 ErdosRenyi：ErdosRenyi.java。

为了方便之后做题，除了 Count() 之外，这个类还包含其他方法，具体可以查看注释。

代码

ErdosRenyi.cs

using System;
using System.Collections.Generic;

namespace UnionFind
{
    /// <summary>
    /// 提供一系列对并查集进行随机测试的静态方法。
    /// </summary>
    public class ErdosRenyi
    {
        /// <summary>
        /// 随机生成一组能让并查集只剩一个连通分量的连接。
        /// </summary>
        /// <param name="n">并查集大小。</param>
        /// <returns>一组能让并查集只剩一个连通分量的连接。</returns>
        public static Connection[] Generate(int n)
        {
            Random random = new Random();
            List<Connection> connections = new List<Connection>();
            WeightedQuickUnionPathCompressionUF uf = new WeightedQuickUnionPathCompressionUF(n);

            while (uf.Count() > 1)
            {
                int p = random.Next(n);
                int q = random.Next(n);
                uf.Union(p, q);
                connections.Add(new Connection(p, q));
            }

            return connections.ToArray();
        }

        /// <summary>
        /// 随机生成连接，返回令并查集中只剩一个连通分量所需的连接总数。
        /// </summary>
        /// <param name="uf">用于测试的并查集。</param>
        /// <returns>需要的连接总数。</returns>
        public static int Count(UF uf)
        {
            Random random = new Random();
            int size = uf.Count();
            int edges = 0;
            while (uf.Count() > 1)
            {
                int p = random.Next(size);
                int q = random.Next(size);
                uf.Union(p, q);
                edges++;
            }

            return edges;
        }

        /// <summary>
        /// 使用指定的连接按顺序合并。
        /// </summary>
        /// <param name="uf">需要测试的并查集。</param>
        /// <param name="connections">用于输入的连接集合。</param>
        public static void Count(UF uf, Connection[] connections)
        {
            foreach (Connection c in connections)
            {
                uf.Union(c.P, c.Q);
            }
        }
    }
}

Main 方法：

using System;
using UnionFind;

namespace _1._5._17
{
    /*
     * 1.5.17
     * 
     * 随机链接。
     * 设计 UF 的一个用例 ErdosRenyi，
     * 从命令行接受一个整数 N，在 0 到 N-1 之间产生随机整数对，
     * 调用 connected() 判断它们是否相连，
     * 如果不是则调用 union() 方法（和我们的开发用例一样）。
     * 不断循环直到所有触点均相互连通并打印出生成的连接总数。
     * 将你的程序打包成一个接受参数 N 并返回连接总数的静态方法 count()，
     * 添加一个 main() 方法从命令行接受 N，调用 count() 并打印它的返回值。
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            int N = 10;
            int[] edges = new int[5];
            for (int i = 0; i < 5; ++i)
            {
                var uf = new UF(N);
                Console.WriteLine(N + "\t" + ErdosRenyi.Count(uf));
                N *= 10;
            }
        }
    }
}

1.5.18

题目

随机网格生成器。
编写一个程序 RandomGrid，从命令行接受一个 int 值 N，生成一个 N×N 的网格中的所有连接。
它们的排列随机且方向随机（即 (p q) 和 (q p) 出现的可能性是相等的），将这个结果打印到标准输出中。
可以使用 RandomBag 将所有连接随机排列（请见练习 1.3.34），并使用如右下所示的 Connection 嵌套类来将 p 和 q 封装到一个对象中。
将程序打包成两个静态方法：generate()，接受参数 N 并返回一个连接的数组；main()，从命令行接受参数 N，调用 generate()，便利返回的数组并打印出所有连接。

private class Connection
{
    int p;
    int q;

    public Connection(int p, int q)
    {
        this.p = p;
        this.q = q;
    }
}

解答

具体生成的连接样式见下题，这里给出 RandomGrid 的实现，需要使用 1.3 节中的随机背包辅助。

代码

RandomGrid.cs

using System;
using System.Collections.Generic;

namespace UnionFind
{
    public class RandomGrid
    {
        /// <summary>
        /// 随机生成 n × n 网格中的所有连接。
        /// </summary>
        /// <param name="n">网格边长。</param>
        /// <returns>随机排序的连接。</returns>
        public static RandomBag<Connection> Generate(int n)
        {
            var result = new RandomBag<Connection>();
            var random = new Random();

            // 建立横向连接
            for (int i = 0; i < n; ++i)
            {
                for (int j = 0; j < n - 1; ++j)
                {
                    if (random.Next(10) > 4)
                    {
                        result.Add(new Connection(i * n + j, (i * n) + j + 1));
                    }
                    else
                    {
                        result.Add(new Connection((i * n) + j + 1, i * n + j));
                    }
                }
            }

            // 建立纵向连接
            for (int j = 0; j < n; ++j)
            {
                for (int i = 0; i < n - 1; ++i)
                {
                    if (random.Next(10) > 4)
                    {
                        result.Add(new Connection(i * n + j, ((i + 1) * n) + j));
                    }
                    else
                    {
                        result.Add(new Connection(((i + 1) * n) + j, i * n + j));
                    }
                }
            }

            return result;
        }

        /// <summary>
        /// 随机生成 n × n 网格中的所有连接，返回一个连接数组。
        /// </summary>
        /// <param name="n">网格边长。</param>
        /// <returns>连接数组。</returns>
        public static Connection[] GetConnections(int n)
        {
            RandomBag<Connection> bag = Generate(n);
            List<Connection> connections = new List<Connection>();

            foreach (Connection c in bag)
            {
                connections.Add(c);
            }

            return connections.ToArray();
        }
    }
}

1.5.19

题目

动画。
编写一个 RandomGrid（请见练习 1.5.18）的用例，
和我们开发用例一样使用 UnionFind 来检查触点的连通性并在处理时用 StdDraw 将它们绘出。

解答

最后绘出的图像：

代码

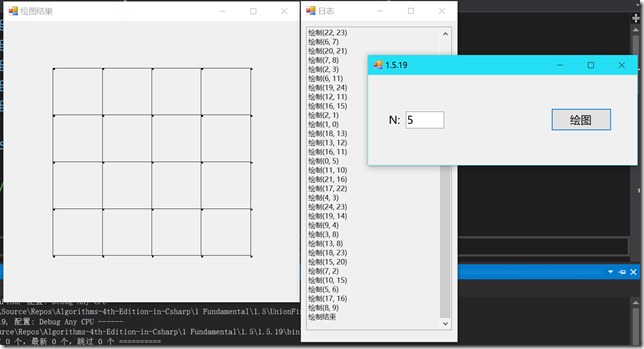
给出绘图部分的代码，窗体部分见 GitHub。

using System;
using System.Drawing;
using System.Collections.Generic;
using System.Windows.Forms;
using UnionFind;

namespace _1._5._19
{
    /*
     * 1.5.19
     * 
     * 动画。
     * 编写一个 RandomGrid（请见练习 1.5.18）的用例，
     * 和我们开发用例一样使用 UnionFind 来检查触点的连通性并在处理时用 StdDraw 将它们绘出。
     * 
     */
    static class Program
    {
        static RandomBag<Connection> bag;
        static Graphics graphics;
        static TextBox logBox;
        static PointF[] points;
        static Timer timer;
        static List<Connection> connections;
        static int count = 0;

        /// <summary>
        /// 应用程序的主入口点。
        /// </summary>
        [STAThread]
        static void Main()
        {
            Application.EnableVisualStyles();
            Application.SetCompatibleTextRenderingDefault(false);
            Application.Run(new Form1());
        }

        /// <summary>
        /// 绘制连接图像。
        /// </summary>
        /// <param name="n">矩阵边长。</param>
        public static void Draw(int n, TextBox log, Log WinBox)
        {
            logBox = log;

            // 生成路径。
            log.AppendText("\r\n开始生成连接……");
            bag = RandomGrid.Generate(n);
            log.AppendText("\r\n生成连接完成");

            // 新建画布窗口。
            log.AppendText("\r\n启动画布……");
            Form2 matrix = new Form2();
            matrix.StartPosition = FormStartPosition.Manual;
            matrix.Location = new Point(WinBox.Left - matrix.ClientRectangle.Width, WinBox.Top);
            matrix.Show();
            log.AppendText("\r\n画布已启动，开始绘图……");
            graphics = matrix.CreateGraphics();

            // 获取绘图区域。
            RectangleF rect = matrix.ClientRectangle;
            float unitX = rect.Width / (n + 1);
            float unitY = rect.Height / (n + 1);

            // 绘制点。
            log.AppendText("\r\n绘制点……");
            points = new PointF[n * n];
            for (int row = 0; row < n; ++row)
            {
                for (int col = 0; col < n; ++col)
                {
                    points[row * n + col] = new PointF(unitX * (col + 1), unitY * (row + 1));
                    graphics.FillEllipse(Brushes.Black, unitX * (col + 1), unitY * (row + 1), 5, 5);
                }
            }
            log.AppendText("\r\n绘制点完成");

            // 绘制连接。
            log.AppendText("\r\n开始绘制连接……");
            connections = new List<Connection>();
            foreach (Connection c in bag)
            {
                connections.Add(c);
            }
            timer = new Timer
            {
                Interval = 500
            };
            timer.Tick += DrawOneLine;
            timer.Start();              
        }

        private static void DrawOneLine(object sender, EventArgs e)
        {
            Connection c = connections[count];
            count++;
            graphics.DrawLine(Pens.Black, points[c.P], points[c.Q]);
            logBox.AppendText("\r\n绘制" + "(" + c.P + ", " + c.Q + ")");
            if (count == bag.Size())
            {
                timer.Stop();
                logBox.AppendText("\r\n绘制结束");
                count = 0;
            }
        }
    }
}

1.5.20

题目

动态生长。
使用链表或大小可变的数组实现加权 quick-union 算法，
去掉需要预先知道对象数量的限制。
为 API 添加一个新方法 newSite()，它应该返回一个类型为 int 的标识符。

解答

将 parent 数组和 size 数组用链表代替即可，很容易实现。

代码

修改后的 WeightedQuickUnionUF.cs

using System;

namespace _1._5._20
{
    /// <summary>
    /// 使用加权 quick-union 算法的并查集。
    /// </summary>
    public class WeightedQuickUnionUF
    {
        protected LinkedList<int> parent;       // 记录各个结点的父级。
        protected LinkedList<int> size;         // 记录各个树的大小。
        protected int count;                    // 分量数目。

        /// <summary>
        /// 建立使用加权 quick-union 的并查集。
        /// </summary>
        /// <param name="n">并查集的大小。</param>
        public WeightedQuickUnionUF()
        {
            this.parent = new LinkedList<int>();
            this.size = new LinkedList<int>();
        }

        /// <summary>
        /// 获取 parent 数组。
        /// </summary>
        /// <returns>parent 数组。</returns>
        public LinkedList<int> GetParent()
        {
            return this.parent;
        }

        /// <summary>
        /// 获取 size 数组。
        /// </summary>
        /// <returns>返回 size 数组。</returns>
        public LinkedList<int> GetSize()
        {
            return this.size;
        }

        /// <summary>
        /// 在并查集中增加一个新的结点。
        /// </summary>
        /// <returns>新结点的下标。</returns>
        public int NewSite()
        {
            this.parent.Insert(this.parent.Size(), this.parent.Size());
            this.size.Insert(1, this.size.Size());
            this.count++;
            return this.parent.Size() - 1;
        }

        /// <summary>
        /// 寻找一个结点所在的连通分量。
        /// </summary>
        /// <param name="p">需要寻找的结点。</param>
        /// <returns>该结点所属的连通分量。</returns>
        public int Find(int p)
        {
            Validate(p);
            while (p != this.parent.Find(p))
            {
                p = this.parent.Find(p);
            }
            return p;
        }

        /// <summary>
        /// 将两个结点所属的连通分量合并。
        /// </summary>
        /// <param name="p">需要合并的结点。</param>
        /// <param name="q">需要合并的另一个结点。</param>
        public void Union(int p, int q)
        {
            int rootP = Find(p);
            int rootQ = Find(q);
            if (rootP == rootQ)
            {
                return;
            }

            if (this.size.Find(rootP) < this.size.Find(rootQ))
            {
                this.parent.Motify(rootP, rootQ);
                this.size.Motify(rootQ, this.size.Find(rootQ) + this.size.Find(rootP));
            }
            else
            {
                this.parent.Motify(rootQ, rootP);
                this.size.Motify(rootP, this.size.Find(rootQ) + this.size.Find(rootP));
            }
            this.count--;
        }

        /// <summary>
        /// 检查输入的 p 是否符合条件。
        /// </summary>
        /// <param name="p">输入的 p 值。</param>
        protected void Validate(int p)
        {
            int n = this.parent.Size();
            if (p < 0 || p >= n)
            {
                throw new ArgumentException("index" + p + " is not between 0 and " + (n - 1));
            }
        }
    }
}

1.5.21

题目

Erd?s-Renyi 模型。
使用练习 1.5.17 的用例验证这个猜想：得到单个连通分量所需生成的整数对数量为 ~1/2NlnN。

解答

给出我电脑上的结果：

实验结果：10
1/2NlnN：11.5129254649702

实验结果：29
1/2NlnN：29.9573227355399

实验结果：132
1/2NlnN：73.7775890822787

实验结果：164
1/2NlnN：175.281065386955

实验结果：418
1/2NlnN：406.013905218706

实验结果：1143
1/2NlnN：922.931359327004

实验结果：2004
1/2NlnN：2067.66981643319

实验结果：4769
1/2NlnN：4578.95382842474

实验结果：10422
1/2NlnN：10045.1360479662

实验结果：21980
1/2NlnN：21864.7288781659

代码

using System;
using UnionFind;

namespace _1._5._21
{
    /*
     * 1.5.21
     * 
     * Erd?s-Renyi 模型。
     * 使用练习 1.5.17 的用例验证这个猜想：
     * 得到单个连通分量所需生成的整数对数量为 ~1/2NlnN。
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            for (int n = 10; n < 10000; n *= 2)
            {
                int total = 0;
                for (int i = 0; i < 100; ++i)
                {
                    UF uf = new UF(n);
                    total += ErdosRenyi.Count(uf);
                }

                Console.WriteLine("实验结果：" + total / 100);
                Console.WriteLine("1/2NlnN：" + Math.Log(n) * n * 0.5);
                Console.WriteLine();
            }
        }
    }
}

1.5.22

题目

Erd?s-Renyi 的倍率实验。
开发一个性能测试用例，从命令行接受一个 int 值 T 并进行 T 次以下实验：
使用练习 1.5.17 的用例生成随机连接，和我们的开发用例一样使用 UnionFind 来检查触点的连通性，不断循环直到所有触点都相互连通。
对于每个 N，打印出 N 值和平均所需的连接数以及前后两次运行时间的比值。
使用你的程序验证正文中的猜想：quick-find 算法和 quick-union 算法的运行时间是平方级别的，加权 quick-union 算法则接近线性级别。

解答

平方级别算法在输入加倍后耗时应该增加四倍，线性则是两倍。

下面给出我电脑上的结果，数据量较大时比较明显：

N:16000
quick-find
平均次数：8452
用时：143 比值：4.46875

quick-union
平均次数：7325
用时：202 比值：3.25806451612903

weighted-quick-union
平均次数：6889
用时：1


N:32000
quick-find
平均次数：15747
用时：510 比值：3.56643356643357

quick-union
平均次数：15108
用时：801 比值：3.96534653465347

weighted-quick-union
平均次数：17575
用时：3 比值：3


N:64000
quick-find
平均次数：33116
用时：2069 比值：4.05686274509804

quick-union
平均次数：38608
用时：4635 比值：5.78651685393258

weighted-quick-union
平均次数：34850
用时：6 比值：2

代码

using System;
using System.Diagnostics;
using UnionFind;

namespace _1._5._22
{
    /*
     * 1.5.22
     * 
     * Erd?s-Renyi 的倍率实验。
     * 开发一个性能测试用例，
     * 从命令行接受一个 int 值 T 并进行 T 次以下实验：
     * 使用练习 1.5.17 的用例生成随机连接，
     * 和我们的开发用例一样使用 UnionFind 来检查触点的连通性，
     * 不断循环知道所有触点都相互连通。
     * 对于每个 N，打印出 N 值和平均所需的连接数以及前后两次运行时间的比值。
     * 使用你的程序验证正文中的猜想：
     * quick-find 算法和 quick-union 算法的运行时间是平方级别的，
     * 加权 quick-union 算法则接近线性级别。
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            long lastTimeQuickFind = 0;
            long lastTimeQuickUnion = 0;
            long lastTimeWeightedQuickUnion = 0;

            long nowTime = 0;
            for (int n = 2000; n < 100000; n *= 2)
            {
                Console.WriteLine("N:" + n);
                QuickFindUF quickFindUF = new QuickFindUF(n);
                QuickUnionUF quickUnionUF = new QuickUnionUF(n);
                WeightedQuickUnionUF weightedQuickUnionUF = new WeightedQuickUnionUF(n);

                // quick-find
                Console.WriteLine("quick-find");
                nowTime = RunTest(quickFindUF);
                if (lastTimeQuickFind == 0)
                {
                    Console.WriteLine("用时：" + nowTime);
                    lastTimeQuickFind = nowTime;
                }
                else
                {
                    Console.WriteLine("用时：" + nowTime + 
                        " 比值：" + (double)nowTime / lastTimeQuickFind);
                    lastTimeQuickFind = nowTime;
                }
                Console.WriteLine();

                // quick-union
                Console.WriteLine("quick-union");
                nowTime = RunTest(quickUnionUF);
                if (lastTimeQuickUnion == 0)
                {
                    Console.WriteLine("用时：" + nowTime);
                    lastTimeQuickUnion = nowTime;
                }
                else
                {
                    Console.WriteLine("用时：" + nowTime + 
                        " 比值：" + (double)nowTime / lastTimeQuickUnion);
                    lastTimeQuickUnion = nowTime;
                }
                Console.WriteLine();

                // weighted-quick-union
                Console.WriteLine("weighted-quick-union");
                nowTime = RunTest(weightedQuickUnionUF);
                if (lastTimeWeightedQuickUnion == 0)
                {
                    Console.WriteLine("用时：" + nowTime);
                    lastTimeWeightedQuickUnion = nowTime;
                }
                else
                {
                    Console.WriteLine("用时：" + nowTime + 
                        " 比值：" + (double)nowTime / lastTimeWeightedQuickUnion);
                    lastTimeWeightedQuickUnion = nowTime;
                }
                Console.WriteLine();

                Console.WriteLine();
            }
            
        }

        /// <summary>
        /// 进行若干次随机试验，输出平均 union 次数，返回平均耗时。
        /// </summary>
        /// <param name="uf">用于测试的并查集。</param>
        /// <returns>平均耗时。</returns>
        static long RunTest(UF uf)
        {
            Stopwatch timer = new Stopwatch();
            int total = 0;
            int repeatTime = 10;
            timer.Start();
            for (int i = 0; i < repeatTime; ++i)
            {
                total += ErdosRenyi.Count(uf);
            }
            timer.Stop();
            Console.WriteLine("平均次数：" + total / repeatTime);

            return timer.ElapsedMilliseconds / repeatTime;
        }
    }
}

1.5.23

题目

在 Erd?s-Renyi 模型下比较 quick-find 算法和 quick-union 算法。
开发一个性能测试用例，从命令行接受一个 int 值 T 并进行 T 次以下实验：使用练习 1.5.17 的用例生成随机连接。
保存这些连接并和我们的开发用例一样分别用 quick-find 和 quick-union 算法检查触点的连通性，不断循环直到所有触点均相互连通。
对于每个 N，打印出 N 值和两种算法的运行时间比值。

解答

先用速度最快的 WeightedQuickUnionUF 生成一系列连接，保存后用这些连接进行测试，生成连接的方法见 1.5.17 的解答。

下面给出我电脑上的结果：

N:2000
quick-find 耗时（毫秒）：4
quick-union 耗时（毫秒）：5
比值：0.8

N:4000
quick-find 耗时（毫秒）：19
quick-union 耗时（毫秒）：24
比值：0.791666666666667

N:8000
quick-find 耗时（毫秒）：57
quick-union 耗时（毫秒）：74
比值：0.77027027027027

N:16000
quick-find 耗时（毫秒）：204
quick-union 耗时（毫秒）：307
比值：0.664495114006515

N:32000
quick-find 耗时（毫秒）：1127
quick-union 耗时（毫秒）：1609
比值：0.700435052827843

代码

using System;
using System.Diagnostics;
using UnionFind;

namespace _1._5._23
{
    /*
     * 1.5.23
     * 
     * 在 Erd?s-Renyi 模型下比较 quick-find 算法和 quick-union 算法。
     * 开发一个性能测试用例，从命令行接受一个 int 值 T 并进行 T 次以下实验：
     * 使用练习 1.5.17 的用例生成随机连接。
     * 保存这些连接并和我们的开发用例一样分别用 quick-find 和 quick-union 算法检查触点的连通性，
     * 不断循环直到所有触点均相互连通。
     * 对于每个 N，打印出 N 值和两种算法的运行时间比值。
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            int n = 1000;
            for (int t = 0; t < 5; ++t)
            {
                Connection[] input = ErdosRenyi.Generate(n);
                QuickFindUF quickFind = new QuickFindUF(n);
                QuickUnionUF quickUnion = new QuickUnionUF(n);

                Console.WriteLine("N:" + n);

                long quickFindTime = RunTest(quickFind, input);
                long quickUnionTime = RunTest(quickUnion, input);

                Console.WriteLine("quick-find 耗时（毫秒）：" + quickFindTime);
                Console.WriteLine("quick-union 耗时（毫秒）：" + quickUnionTime);
                Console.WriteLine("比值：" + (double)quickFindTime / quickUnionTime);
                Console.WriteLine();

                n *= 2;
            }
        }

        /// <summary>
        /// 进行若干次随机试验，输出平均 union 次数，返回平均耗时。
        /// </summary>
        /// <param name="uf">用于测试的并查集。</param>
        /// <param name="connections">用于测试的输入。</param>
        /// <returns>平均耗时。</returns>
        static long RunTest(UF uf, Connection[] connections)
        {
            Stopwatch timer = new Stopwatch();
            int repeatTime = 5;
            timer.Start();
            for (int i = 0; i < repeatTime; ++i)
            {
                ErdosRenyi.Count(uf, connections);
            }
            timer.Stop();

            return timer.ElapsedMilliseconds / repeatTime;
        }
    }
}

1.5.24

题目

适用于 Erd?s-Renyi 模型的快速算法。
在练习1.5.23 的测试中增加加权 quick-union 算法和使用路径压缩的加权 quick-union 算法。
你能分辨出这两种算法的区别吗？

解答

根据上题的代码略作修改即可，路径压缩大概可以快 1/3。

N:10000
加权 quick-find 耗时（毫秒）：9
带路径压缩的加权 quick-union 耗时（毫秒）：6
比值：1.5

N:20000
加权 quick-find 耗时（毫秒）：12
带路径压缩的加权 quick-union 耗时（毫秒）：8
比值：1.5

N:40000
加权 quick-find 耗时（毫秒）：18
带路径压缩的加权 quick-union 耗时（毫秒）：12
比值：1.5

N:80000
加权 quick-find 耗时（毫秒）：36
带路径压缩的加权 quick-union 耗时（毫秒）：30
比值：1.2

N:160000
加权 quick-find 耗时（毫秒）：67
带路径压缩的加权 quick-union 耗时（毫秒）：41
比值：1.63414634146341

代码

using System;
using UnionFind;
using System.Diagnostics;

namespace _1._5._24
{
    /*
     * 1.5.24
     * 
     * 适用于 Erd?s-Renyi 模型的快速算法。
     * 在练习1.5.23 的测试中增加加权 quick-union 算法和使用路径压缩的加权 quick-union 算法。
     * 你能分辨出这两种算法的区别吗？
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            int n = 5000;
            for (int t = 0; t < 5; ++t)
            {
                var input = ErdosRenyi.Generate(n);
                var weightedQuickUnionUF = new WeightedQuickUnionUF(n);
                var weightedQuickUnionPathCompressionUF = new WeightedQuickUnionPathCompressionUF(n);

                Console.WriteLine("N:" + n);

                long weightedQuickUnionTime = RunTest(weightedQuickUnionUF, input);
                long weightedQuickUnionPathCompressionTime = RunTest(weightedQuickUnionPathCompressionUF, input);

                Console.WriteLine("加权 quick-find 耗时（毫秒）：" + weightedQuickUnionTime);
                Console.WriteLine("带路径压缩的加权 quick-union 耗时（毫秒）：" + weightedQuickUnionPathCompressionTime);
                Console.WriteLine("比值：" + (double)weightedQuickUnionTime / weightedQuickUnionPathCompressionTime);
                Console.WriteLine();

                n *= 2;
            }
        }

        /// <summary>
        /// 进行若干次随机试验，输出平均 union 次数，返回平均耗时。
        /// </summary>
        /// <param name="uf">用于测试的并查集。</param>
        /// <param name="connections">用于测试的输入。</param>
        /// <returns>平均耗时。</returns>
        static long RunTest(UF uf, Connection[] connections)
        {
            Stopwatch timer = new Stopwatch();
            int repeatTime = 5;
            timer.Start();
            for (int i = 0; i < repeatTime; ++i)
            {
                ErdosRenyi.Count(uf, connections);
            }
            timer.Stop();

            return timer.ElapsedMilliseconds / repeatTime;
        }
    }
}

1.5.25

题目

随机网格的倍率测试。
开发一个性能测试用例，从命令行接受一个 int 值 T 并进行 T 次以下实验：
使用练习 1.5.18 的用例生成一个 N×N 的随机网格，所有连接的方向随机且排列随机。
和我们的开发用例一样使用 UnionFind 来检查触点的连通性，不断循环直到所有触点均相互连通。
对于每个 N，打印出 N 值和平均所需的连接数以及前后两次运行时间的比值。
使用你的程序验证正文中的猜想：quick-find 和 quick-union 算法的运行时间是平方级别的，加权 quick-union 算法则接近线性级别。
注意：随着 N 值加倍，网格中触点的数量会乘以 4，因此平方级别的算法运行时间会变为原来的 16 倍，线性级别的算法的运行时间则变为原来的 4 倍。

解答

略微修改 1.5.22 的代码即可。

我电脑上的结果：

Quick-Find
N:1600
平均用时（毫秒）：4
N:6400
平均用时（毫秒）：67    比值：16.75
N:25600
平均用时（毫秒）：1268  比值：18.9253731343284
N:102400
平均用时（毫秒）：20554 比值：16.2097791798107
Quick-Union
N:1600
平均用时（毫秒）：5     比值：0.000243261652233142
N:6400
平均用时（毫秒）：66    比值：13.2
N:25600
平均用时（毫秒）：1067  比值：16.1666666666667
N:102400
平均用时（毫秒）：18637 比值：17.4667291471415
Weighted Quick-Union
N:1600
平均用时（毫秒）：0     比值：0
N:6400
平均用时（毫秒）：2
N:25600
平均用时（毫秒）：12    比值：6
N:102400
平均用时（毫秒）：64    比值：5.33333333333333

代码

using System;
using System.Diagnostics;
using UnionFind;

namespace _1._5._25
{
    /*
     * 1.5.25
     * 
     * 随机网格的倍率测试。
     * 开发一个性能测试用例，
     * 从命令行接受一个 int 值 T 并进行 T 次以下实验：
     * 使用练习 1.5.18 的用例生成一个 N×N 的随机网格，
     * 所有连接的方向随机且排列随机。
     * 和我们的开发用例一样使用 UnionFind 来检查触点的连通性，
     * 不断循环直到所有触点均相互连通。
     * 对于每个 N，打印出 N 值和平均所需的连接数以及前后两次运行时间的比值。
     * 使用你的程序验证正文中的猜想：
     * quick-find 和 quick-union 算法的运行时间是平方级别的，
     * 加权 quick-union 算法则接近线性级别。
     * 
     * 注意：随着 N 值加倍，网格中触点的数量会乘以 4，
     * 因此平方级别的算法运行时间会变为原来的 16 倍，
     * 线性级别的算法的运行时间则变为原来的 4 倍
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            int n = 40;
            int t = 4;

            // quick-find
            Console.WriteLine("Quick-Find");
            long last = 0;
            long now = 0;
            for (int i = 0; i < t; ++i, n *= 2)
            {
                Console.WriteLine("N:" + n * n);
                var connections = RandomGrid.GetConnections(n);

                QuickFindUF quickFind = new QuickFindUF(n * n);
                now = RunTest(quickFind, connections);
                if (last == 0)
                {
                    Console.WriteLine("平均用时（毫秒）：" + now);
                    last = now;
                }
                else
                {
                    Console.WriteLine("平均用时（毫秒）：" + now + "\t比值：" + (double)now / last);
                    last = now;
                }
            }

            // quick-union
            Console.WriteLine("Quick-Union");
            n = 40;
            for (int i = 0; i < t; ++i, n *= 2)
            {
                Console.WriteLine("N:" + n * n);
                var connections = RandomGrid.GetConnections(n);

                QuickUnionUF quickFind = new QuickUnionUF(n * n);
                now = RunTest(quickFind, connections);
                if (last == 0)
                {
                    Console.WriteLine("平均用时（毫秒）：" + now);
                    last = now;
                }
                else
                {
                    Console.WriteLine("平均用时（毫秒）：" + now + "\t比值：" + (double)now / last);
                    last = now;
                }
            }

            // 加权 quick-union
            Console.WriteLine("Weighted Quick-Union");
            n = 40;
            for (int i = 0; i < t; ++i, n *= 2)
            {
                Console.WriteLine("N:" + n * n);
                var connections = RandomGrid.GetConnections(n);

                WeightedQuickUnionUF quickFind = new WeightedQuickUnionUF(n * n);
                now = RunTest(quickFind, connections);
                if (last == 0)
                {
                    Console.WriteLine("平均用时（毫秒）：" + now);
                    last = now;
                }
                else
                {
                    Console.WriteLine("平均用时（毫秒）：" + now + "\t比值：" + (double)now / last);
                    last = now;
                }
            }
        }

        /// <summary>
        /// 进行若干次随机试验，输出平均 union 次数，返回平均耗时。
        /// </summary>
        /// <param name="uf">用于测试的并查集。</param>
        /// <param name="connections">用于测试的输入。</param>
        /// <returns>平均耗时。</returns>
        static long RunTest(UF uf, Connection[] connections)
        {
            Stopwatch timer = new Stopwatch();
            long repeatTime = 3;
            timer.Start();
            for (int i = 0; i < repeatTime; ++i)
            {
                ErdosRenyi.Count(uf, connections);
            }
            timer.Stop();

            return timer.ElapsedMilliseconds / repeatTime;
        }
    }
}

1.5.26

题目

Erd?s-Renyi 模型的均摊成本图像。
开发一个用例，从命令行接受一个 int 值 N，在 0 到 N-1 之间产生随机整数对，调用 connected() 判断它们是否相连，如果不是则用 union() 方法（和我们的开发用例一样）。
不断循环直到所有触点互通。
按照正文的样式将所有操作的均摊成本绘制成图像。

解答

和 1.5.16 的程序类似，将测试的内容改为 Erdos-Renyi 即可。

样例输出：

代码

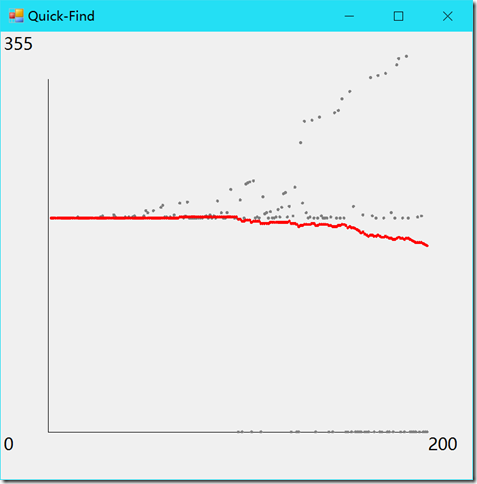
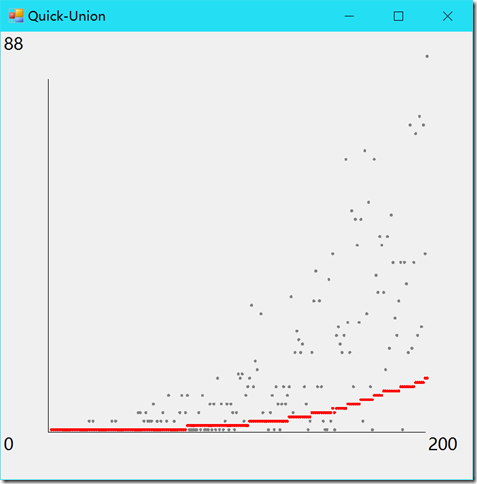
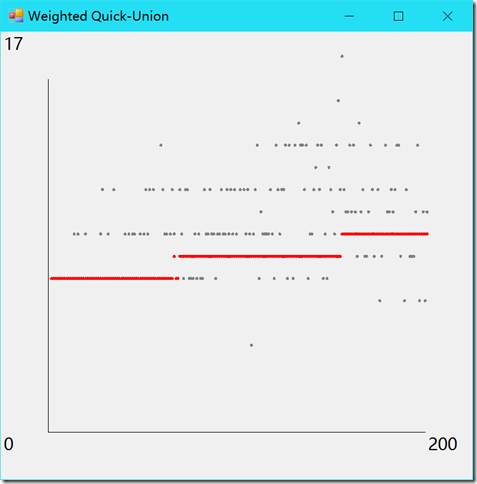
using System;
using System.Linq;
using System.Windows.Forms;
using System.Drawing;
using UnionFind;

namespace _1._5._26
{
    /*
     * 1.5.26
     * 
     * Erd?s-Renyi 模型的均摊成本图像。
     * 开发一个用例，
     * 从命令行接受一个 int 值 N，在 0 到 N-1 之间产生随机整数对，
     * 调用 connected() 判断它们是否相连，
     * 如果不是则用 union() 方法（和我们的开发用例一样）。
     * 不断循环直到所有触点互通。
     * 按照正文的样式将所有操作的均摊成本绘制成图像。
     * 
     */
    static class Program
    {
        /// <summary>
        /// 应用程序的主入口点。
        /// </summary>
        [STAThread]
        static void Main()
        {
            Application.EnableVisualStyles();
            Application.SetCompatibleTextRenderingDefault(false);
            Compute();
            Application.Run(new Form1());
        }

        static void Compute()
        {
            int size = 200;
            QuickFindUF quickFind = new QuickFindUF(size);
            QuickUnionUF quickUnion = new QuickUnionUF(size);
            WeightedQuickUnionUF weightedQuickUnion = new WeightedQuickUnionUF(size);
            Connection[] connections = ErdosRenyi.Generate(size);

            int[] quickFindResult = new int[size];
            int[] quickUnionResult = new int[size];
            int[] weightedQuickUnionResult = new int[size];
            int p, q;
            for (int i = 0; i < size; ++i)
            {
                p = connections[i].P;
                q = connections[i].Q;

                quickFind.Union(p, q);
                quickUnion.Union(p, q);
                weightedQuickUnion.Union(p, q);
                quickFindResult[i] = quickFind.ArrayVisitCount;
                quickUnionResult[i] = quickUnion.ArrayVisitCount;
                weightedQuickUnionResult[i] = weightedQuickUnion.ArrayParentVisitCount + weightedQuickUnion.ArraySizeVisitCount;

                quickFind.ResetArrayCount();
                quickUnion.ResetArrayCount();
                weightedQuickUnion.ResetArrayCount();
            }

            Draw(quickFindResult, "Quick-Find");
            Draw(quickUnionResult, "Quick-Union");
            Draw(weightedQuickUnionResult, "Weighted Quick-Union");
        }

        static void Draw(int[] cost, string title)
        {
            // 构建 total 数组。
            int[] total = new int[cost.Length];
            total[0] = cost[0];
            for (int i = 1; i < cost.Length; ++i)
            {
                total[i] = total[i - 1] + cost[i];
            }

            // 获得最大值。
            int costMax = cost.Max();

            // 新建绘图窗口。
            Form2 plot = new Form2();
            plot.Text = title;
            plot.Show();
            Graphics graphics = plot.CreateGraphics();

            // 获得绘图区矩形。
            RectangleF rect = plot.ClientRectangle;
            float unitX = rect.Width / 10;
            float unitY = rect.Width / 10;

            // 添加 10% 边距作为文字区域。
            RectangleF center = new RectangleF
                (rect.X + unitX, rect.Y + unitY,
                rect.Width - 2 * unitX, rect.Height - 2 * unitY);

            // 绘制坐标系。
            graphics.DrawLine(Pens.Black, center.Left, center.Top, center.Left, center.Bottom);
            graphics.DrawLine(Pens.Black, center.Left, center.Bottom, center.Right, center.Bottom);
            graphics.DrawString(costMax.ToString(), plot.Font, Brushes.Black, rect.Location);
            graphics.DrawString(cost.Length.ToString(), plot.Font, Brushes.Black, center.Right, center.Bottom);
            graphics.DrawString("0", plot.Font, Brushes.Black, rect.Left, center.Bottom);

            // 初始化点。
            PointF[] grayPoints = new PointF[cost.Length];
            PointF[] redPoints = new PointF[cost.Length];
            unitX = center.Width / cost.Length;
            unitY = center.Width / costMax;

            for (int i = 0; i < cost.Length; ++i)
            {
                grayPoints[i] = new PointF(center.Left + unitX * (i + 1), center.Bottom - (cost[i] * unitY));
                redPoints[i] = new PointF(center.Left + unitX * (i + 1), center.Bottom - ((total[i] / (i + 1)) * unitY));
            }

            // 绘制点。
            for (int i = 0; i < cost.Length; ++i)
            {
                graphics.FillEllipse(Brushes.Gray, new RectangleF(grayPoints[i], new SizeF(5, 5)));
                graphics.FillEllipse(Brushes.Red, new RectangleF(redPoints[i], new SizeF(5, 5)));
            }

            graphics.Dispose();
        }
    }
}